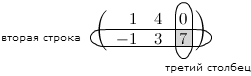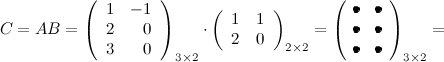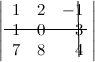- Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
- Пример решения системы линейных уравнений с помощью метода обратной матрицы
- Квадратные СЛАУ. Матричный метод решения
- Матричный метод решения
- Примеры решения систем уравнений
- Примеры решения задач с матрицами
- Примеры по темам:
- Матрицы: основные определения и понятия
- Умножение матрицы на число
- Сложение и вычитание матриц
- Умножение матриц
- Транспонирование матрицы
- Минор и алгебраическое дополнение
- Вычисление определителя
- Нахождение обратной матрицы
- Нахождение ранга матрицы
Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы
В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.
Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.
Найти решение системы n линейных уравнений с n неизвестными:
a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n
Матричный вид записи: А × X = B
где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.
X = x 1 x 2 ⋮ x n — столбец неизвестных,
B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.
Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :
A — 1 × A × X = A — 1 × B .
Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .
Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .
В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.
Пример решения системы линейных уравнений с помощью метода обратной матрицы
Решаем СЛАУ методом обратной матрицы:
2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2
- Записываем систему в виде матричного уравнения А X = B , где
А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .
- Выражаем из этого уравнения X :
- Находим определитель матрицы А :
d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25
d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.
- Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :
А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,
А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,
А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,
А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,
А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,
А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,
А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,
А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,
А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .
- Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :
А * = — 6 7 5 17 1 — 10 — 10 — 5 0
- Записываем обратную матрицу согласно формуле:
A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,
- Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:
X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1
Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1
Источник
Квадратные СЛАУ. Матричный метод решения
С помощью данного метода можно находить решение только для квадратных СЛАУ.
Матричный метод решения
Запишем заданную систему в матричном виде:
Если матрица $$A$$ невырождена, то тогда с помощью операций над матрицами выразим неизвестную матрицу $$X$$ . Операция деления на множестве матриц заменена умножением на обратную матрицу, поэтому домножим последнее равенство на матрицу $A^<-1>$ слева:
$$A^ <-1>A X=A^ <-1>B \Rightarrow E X=A^ <-1>B \Rightarrow$$ $$X=A^ <-1>B$$
Поэтому, чтобы найти неизвестную матрицу $$X$$ надо найти обратную матрицу к матрице системы и умножить ее справа на вектор-столбец свободных коэффициентов.
Данный метод удобно применять тогда, когда нужно решить много одинаковых систем с разными правыми частями.
Примеры решения систем уравнений
Задание. Найти решение СЛАУ $\left\<\begin
$$X=\left(\begin
Две матрицы одного размера равны, если равны их соответствующие элементы, то есть в итоге имеем, что $x_<1>=-11, x_<2>=31$
Ответ. $x_<1>=-11, x_<2>=31$
Квадратные СЛАУ. Матричный метод решения не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Решить с помощью обратной матрицы систему $\left\<\begin
Решение. Запишем данную систему в матричной форме:
где $A=\left(\begin
Найдем обратную матрицу $X=A^<-1>$ к матрице $A$ с помощью союзной матрицы:
Здесь $\Delta=|A|$ — \lt a href=»formules_6_11.php» title=»Методы вычисления определителей матрицы: теоремы и примеры нахождения»>определитель матрицы $A$ ; матрица $\tilde$ — союзная матрица, она получена из исходной матрицы $A$ заменой ее элементов их алгебраическими дополнениями. Найдем $A$ , для этого вычислим алгебраические дополнения к элементам матрицы $A$ :
Определитель матрицы $A$
$$\Delta=\left|\begin
Источник
Примеры решения задач с матрицами
Матрицы широко применяются в математике для компактной записи СЛАУ или систем дифференциальных уравнений. Тогда количество строк матрицы соответствует количеству уравнений системы, а количество столбцов равно количеству неизвестных. Матричный аппарат позволяет свести решение громоздких СЛАУ к компактным операциям над матрицами.
На практике, они позволяют не делать лишних операций и сократить время выполнения задач. Поэтому, будущим специалистам очень важно понять теорию матриц и научиться решать задачи с ними. Перед изучением примеров решения задач советуем изучить теоретический материал по матрицам, прочитать все определения и свойства. Список тем находится в правом меню.
Примеры по темам:
Матрицы: основные определения и понятия
Задание. Чему равен элемент $ a_ <23>$ матрицы $ A=\left( \begin
Решение. Находим элемент, который стоит на пересечении второй строки и третьего столбца:
Таким образом, $a_<23>=7$.
Ответ. $a_<23>=7$
Умножение матрицы на число
Теоретический материал по теме — умножение матрицы на число.
Примеры решения задач с матрицами не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Пусть $A=\left( \begin
Ответ. $2 A=\left( \begin
Сложение и вычитание матриц
Теоретический материал по теме — сложение и вычитание матриц.
Задание. Найти матрицу $C=A-3 B$, если $A=\left( \begin
Умножение матриц
Теоретический материал по теме — умножение матриц.
Задание. Вычислить $A B$ и $B A$, если $A=\left( \begin
Решение. Так как $A=A_<3 \times 2>$ , а $B=B_<2 \times 2>$ , то произведение возможно и результатом операции умножения будет матрица $C=C_<3 \times 2>$ , а это матрица вида $C=\left( \begin
Вычисли элементы матрицы $C$ :
$ c_<11>=a_ <11>\cdot b_<11>+a_ <12>\cdot b_<21>=1 \cdot 1+(-1) \cdot 2=-1 $
$ c_<12>=a_ <11>\cdot b_<12>+a_ <12>\cdot b_<22>=1 \cdot 1+(-1) \cdot 0=1 $
$ c_<21>=a_ <21>\cdot b_<11>+a_ <22>\cdot b_<21>=2 \cdot 1+0 \cdot 2=2 $
$ c_<22>=a_ <21>\cdot b_<12>+a_ <22>\cdot b_<22>=2 \cdot 1+0 \cdot 0=2 $
$ c_<31>=a_ <31>\cdot b_<11>+a_ <32>\cdot b_<21>=3 \cdot 1+0 \cdot 2=3 $
$ c_<31>=a_ <31>\cdot b_<12>+a_ <32>\cdot b_<22>=3 \cdot 1+0 \cdot 0=3 $
Выполним произведения в более компактном виде:
Найдем теперь произведение $D=B A=B_ <2 \times 2>\cdot A_<3 \times 2>$. Так как количество столбцов матрицы $B$ (первый сомножитель) не совпадает с количеством строк матрицы $A$ (второй сомножитель), то данное произведение неопределенно. Умножить матрицы в данном порядке невозможно.
Ответ. $A B=\left( \begin
Транспонирование матрицы
Теоретический материал по теме — транспонирование матрицы.
Задание. Найти матрицу $A^
Минор и алгебраическое дополнение
Задание. Найти минор $M_<23>$ к элементу $a_<23>$ определителя $\left| \begin
Решение. Вычеркиваем в заданном определителе вторую строку и третий столбец:
Задание. Найти алгебраическое дополнение $A_<23>$ к элементу $a_<23>$ определителя $\left| \begin
Вычисление определителя
Задание. Вычислить определитель второго порядка $\left| \begin
Решение. $\left| \begin
Задание. Вычислить определитель $\left| \begin
Решение. $\left| \begin
$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$
Задание. Вычислить определитель $\left| \begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Задание. Вычислить определитель $\Delta=\left| \begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $\Delta=-80$
Нахождение обратной матрицы
Задание. Для матрицы $A=\left( \begin
Решение. Приписываем к заданной матрице $A$ справа единичную матрицу второго порядка:
От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):
От второй строки отнимаем две первых:
Первую и вторую строки меняем местами:
От второй строки отнимаем две первых:
Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:
Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.
Таким образом, получаем, что $A^<-1>=\left( \begin
Задание. Найти обратную матрицу для $A=\left( \begin
Решение. Шаг 1. Находим определитель: $\Delta=\left| \begin
Задание. Найти обратную матрицу к матрице $A=\left( \begin
Решение. Вычисляем определитель матрицы:
$\Delta=\left| \begin
$-1 \cdot(-1) \cdot 2-3 \cdot 1 \cdot 1-2 \cdot 0 \cdot(-1)=1+12+0+2-3+0=12 \neq 0$
Так как определитель не равен нулю, то матрица имеет обратную. Обратная матрица $A^<-1>$ к матрице $A$ находится по формуле:
Транспонируем эту матрицу (т.е. строки матрицы делаем столбцами с тем же номером):
Нахождение ранга матрицы
Теоретический материал по теме — нахождение ранга матрицы.
Решение. С помощью элементарных преобразований над ее строками приведем матрицу $A$ к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей — две четвертых:
Ко второй строке прибавим пять первых, к третьей — три третьих:
Меняем местами первую и вторую строчки:
Далее четвертую и первую строки:
Ответ. $\operatorname
Задание. Найти ранг матрицы $A=\left( \begin
Решение. Минорами минимального порядка являются миноры первого порядка, которые равны элементам матрицы $A$ . Рассмотрим, например, минор $M_<1>=1 \neq 0$ . расположенный в первой строке и первом столбце. Окаймляем его с помощью второй строки и второго столбца, получаем минор $M_<2>^<1>=\left| \begin
так как содержит два пропорциональных столбца (первый и второй); второй минор
преобразуем следующим образом: к первой строке прибавим третью, а ко второй две третьих:
И так как первая и вторая строки пропорциональны, то минор равен нулю.
Таким образом, все окаймляющие миноры третьего порядка равны нулю. А, значит, ранг матрицы $A$ равен двум: $\operatorname
Ответ. $\operatorname
Источник