Матрица калькулятор система с минусом 3 способа расчета

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

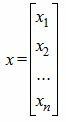(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда

A −1 Ax=A −1 b.

(4)

Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:

Ex=A −1 b.

(4)

или, учитывая, что Ex=x:

x=A −1 b.

(5)

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

.

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

.

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

.

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

.

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

.

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

.

Пример 2. Решить следующую систему линейных уравнений матричным методом:

.

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

.

Вычислим все алгебраические дополнения матрицы A:

,

,

,

,

,

,

,

,

.

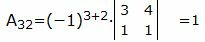Обратная матрица вычисляется из следующего выражения:

где A_ij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

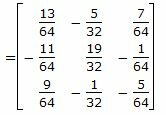Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда

Источник

Онлайн калькулятор. Определитель матрицы. Детерминант матрицы.

Используя этот онлайн калькулятор для вычисления определителя (детерминанта) матриц, вы сможете очень просто и быстро найти определитель (детерминант) матрицы.

Воспользовавшись онлайн калькулятором для вычисления определителя (детерминанта) матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на транспонирование матриц, а также закрепить пройденный материал.

Найти определитель (детерминант) матрицы

Введите значения Матрицы:

Ввод данных в калькулятор для вычисления определителя (детерминанта) матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления определителя (детерминанта) матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Определитель (детерминант) матрицы.

Вычисление определителя матрицы 2×2

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

a 11 a 12 a 21 a 22

= a 11· a 22 — a 12· a 21

Правило треугольника для вычисления определителя матрицы 3×3

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.

+	–

∆ =

a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33

=

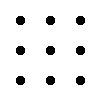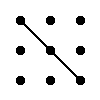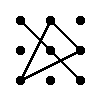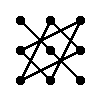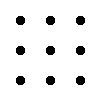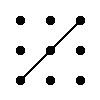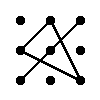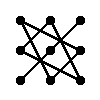Вычисление определителя матрицы произвольного размера

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Источник

Онлайн калькулятор. Сложение и вычитание матриц.

Используя этот онлайн калькулятор для сложения и вычитания матриц, вы сможете очень просто и быстро найти сумму двух матриц или разность двух матриц.

Воспользовавшись онлайн калькулятором для сложения и вычитания матриц, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на сложение и вычитание матриц, а также закрепить пройденный материал.

Калькулятор сложения и вычитания матриц

Введите значения матриц:

Ввод данных в калькулятор для сложения и вычитания матриц

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для сложения и вычитания матриц

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Сложение и вычитание матриц.

Сложение матриц (сумма матриц) A + B есть операция вычисления матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен:

Вычитание матриц (разность матриц) A — B есть операция вычисления матрицы C, все элементы которой равны попарной разности всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Источник

Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) матричным методом (методом обратной матрицы), вы сможете очень просто и быстро найти решение системы.

Воспользовавшись онлайн калькулятором для решения систем линейных уравнений матричным методом (методом обратной матрицы), вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Решить систему линейных уравнений матричным методом

Изменить названия переменных в системе

Заполните систему линейных уравнений:

Ввод данных в калькулятор для решения систем линейных уравнений матричным методом

• В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
• Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа.
• Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
• Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.

Например, линейное уравнение x ₁ — 7 x ₂ — x ₄ = 2

будет вводится в калькулятор следующим образом:

Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом

• Между полями для ввода можно перемещаться нажимая клавиши «влево», «вправо», «вверх» и «вниз» на клавиатуре.
• Вместо x ₁, x ₂, . вы можете ввести свои названия переменных.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Источник

Решение задач с матрицами.

Матричный калькулятор

Очистить	Размер ×
Транспонировать	Умножить на
Найти определитель	Возвести в степень
Найти ранг	Найти обратную

Очистить	Размер ×
Транспонировать	Умножить на
Найти определитель	Возвести в степень
Найти ранг	Найти обратную

Ввод данных в матричный калькулятор

В матричный калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности матричного калькулятора

• Между полями для ввода можно перемещаться нажимая клавиши , , и на клавиатуре.

Теория. Матрицы

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник