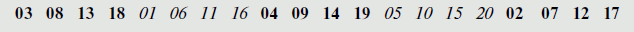Матричный алгоритм шифрования

Автор: Саломатин Кирилл Сергеевич

Опубликовано: 24.04.2012
Исправлено: 10.12.2016
Версия текста: 1.1

Введение Постановка задачи Современные алгоритмы Новый класс алгоритмов Шифрование Дешифрование Особенности алгоритма Вывод Список литературы

Введение

Приносим читателям свои извинения за публикацию этой статьи. Статья очень плоха, см. подробнее в обсуждении на форуме. Торопились сдать номер, понадеялись на автора, недоглядели. Ещё раз извините.

Система определения движущихся объектов является довольно востребованной, т.к. помогает облегчить задачу многим службам, например, авиадиспетчерам. Но, как и в любой системе, в системе определения движущихся объектов необходимо производить шифрование информации на пути от датчика до системы анализа полученных данных.

Постановка задачи

Необходимо разработать алгоритм шифрования данных для системы определения движущихся объектов.

Современные алгоритмы

На данный момент самыми распространенными классами алгоритмов являются симметричные алгоритмы и асимметричные, т.е. системы с открытым ключом.

На рис.1-4 представлена схема работы симметричного алгоритма шифрования AES, который является государственным стандартом шифрования США с 2001года:

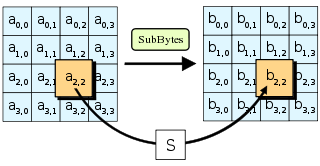
Рис.1 «Шаг 1»

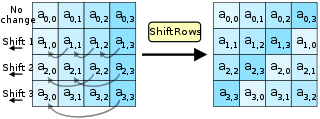
Рис.2 «Шаг 2»

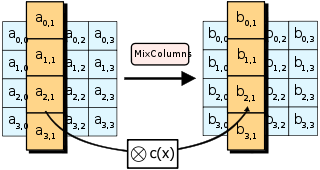
Рис.3 «Шаг 3»

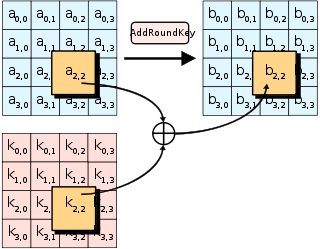
Рис.4 «Шаг 4»

Еще одним из распространенных алгоритмов является асимметричный алгоритм, или система с открытым ключом.

Идея криптографии с открытым ключом очень тесно связана с идеей односторонних функций, то есть таких функций f(x), что по известному x довольно просто найти значение f(x), тогда как определить x из f(x) невозможно. Поэтому криптография с открытым ключом использует односторонние функции с лазейкой. Лазейка — это некий секрет, который помогает расшифровать текст. То есть существует такой y, что зная f(x) и y, можно вычислить x. К примеру, если разобрать часы на множество составных частей, то очень сложно собрать вновь работающие часы. Но если есть инструкция по сборке (лазейка), то можно легко решить эту проблему.

Новый класс алгоритмов

В данной работе представлен новый класс алгоритмов. В отличие от описанных алгоритмов, в данном применяется новый подход к кодированию информации.

Шифрование

1. Удалить повторяющиеся символы и сохранить количество повторений и номера позиций этих символов в тексте (эти данные составляют ключи.)
2. Вычислить номер символа в таблице ASCII.
3. ASCII представляет собой кодировку для представления десятичных цифр, латинского и национального алфавитов, знаков препинания и управляющих символов.
4. Построить 3 матрицы, где одна матрица – номера символов текста, вторая состоит из количества повторений этих символов, а третья состоит из номеров позиций символов в тексте, где каждая срока соответствует одному символу.
5. Перемножить первые 2 матрицы. После этого действия должна получиться квадратная матрица, т.к. при дешифровании необходимо будет найти обратную матрицу, которую необходимо будет умножить на матрицу повторений.
6. Перемешать текст по правилу: первая позиция – номер позиции элемента, вторая позиция – символ из п.4, а на 3-м – количество повторений.
7. Произвести гаммирование полученного текста.

Гаммирование – преобразование исходного (открытого) текста, при котором символы исходного текста складываются (по модулю, равному мощности алфавита) с символами псевдослучайной последовательности, вырабатываемой по определенному правилу. Гамма в криптографии – псевдослучайная числовая последовательность, вырабатываемая по определенному алгоритму и используемая для зашифровывания открытых данных и расшифровывания зашифрованных данных. Наложение гаммы происходит по формуле αi=βi+γi(mod n), где βi – исходный текст, γi – гамма, n – основание используемого алфавита, αi – результат.

Дешифрование

1. Произвести гаммирование. Особенность гаммирования в том, что если произвести над шифротекстом повторное гаммирование, то получится исходный текст.
2. Полученный текст необходимо разбить на 3 части по правилу, используемому при шифровании. Получится 3 матрицы – шифротекст, количество повторений и номера позиций.
3. Необходимо найти обратную матрицу шифротекста и перемножить её с матрицей повторений.
4. Теперь необходимо полученную матрицу перевести в символы и сопоставить с матрицей повторений и матрицей позиций. И в итоге получится исходный текст.

Особенности алгоритма

1. Динамическое формирование ключей. Ключи формируются только для конкретного момента и данных и для других данных они не подходит.
2. Изменение одного символа в исходном тексте приводит к полному изменению зашифрованного текста.
3. Данный алгоритм имеет составной ключ, состоящий из двух частей и для дешифрации необходимо наличие всех частей.
4. Изменение одного символа в исходном тексте приводит к полному изменению зашифрованного текста.
5. Исходный и финальный тексты не совместимы ни по чтению, ни по длине. Данное свойство не позволяет напрямую, простыми методами подобрать исходный текст.
6. Отсутствие циклов в работе алгоритма.
7. Использование данного алгоритма не позволяет подобрать ключи, отличные от реальных, такие, что позволяют получить исходный текст.

Вывод

Сфера деятельности современных алгоритмов четко разделена – асимметричные алгоритмы применяются в основном в сетевых протоколах, а симметричные применяется во всем остальном.

Представленный же здесь алгоритм, в связи со своей динамичностью, универсален и может применяться не только в системе обнаружения движущихся объектов, но и в любой другой.

Источник

Матричный метод шифрования

выберим матрицу А(4,4)
открытый объект: Меня зовут Иван

закрытый объект: м увезтано няи

Помогите пожалуйста написать код.
Вот что у меня получилось:

Метод шифрования
всем привет. подскажите, каким методом шифрования получено значение.

Метод шифрования RSA
помогите найти ошибку, код не правильно работает 6

Решение

спасибо, но тут создается матрица автоматически относительно длинны строки, я правильно понял? Например если длина строки равно 255, то размер матрицы будет равно 15 приблизительно.
А можно, так, чтобы например матрица была размером 5х5 и использовалась до последнего символа текста.
Примерно так:

Решение

Матричный метод решения системы
Матричным методом решить системы.Что не так?? Не могу понять как правельно сделать. k=4; U=;.

Матричный метод решения СЛАУ
Доброго времени суток. Нужно решить систему линейных уравнений с 4-мя переменными матричным.

Матричный метод решения СЛАУ
Здравствуйте уважаемые програмисты, не могу осилить данный метод, и в нете инфы очень мало, может у.

Как можно найти алгебраическое дополнение в матрице (матричный метод, СЛАУ)
Здравствуйте! Подскажите,пожалуйста, как можно найти алгебраическое дополнение в матрице(матричный.

Источник

Традиционные шифры с симметричным ключом

Объединение двух подходов

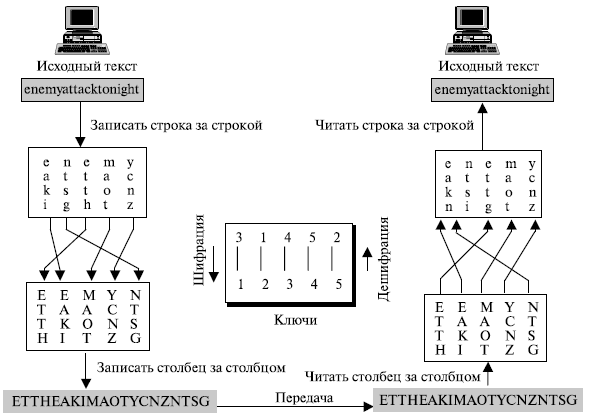
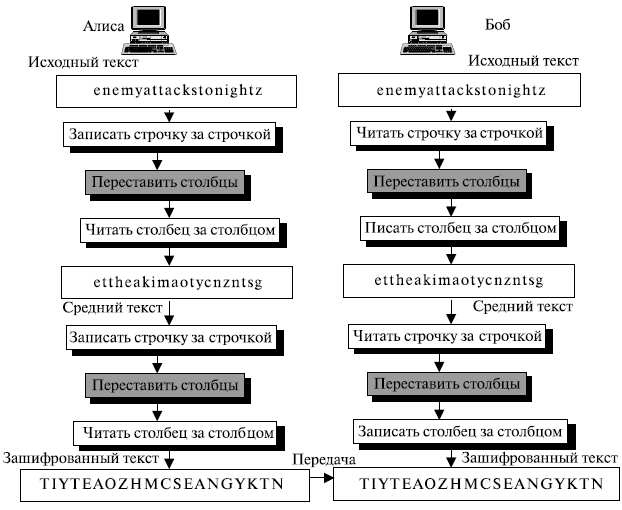
Современные шифры перестановки, чтобы достигнуть лучшего скремблирования, объединяют два подхода. Шифрование и дешифрование делается в три шага. Первый: текст пишется таблицей строка за строкой. Второй: делается перестановка, изменяя порядок следования столбцов. Третий: столбец за столбцом читается новая таблица. Первые и третьи шаги обеспечивают бесключевое глобальное изменение порядка следования; второй шаг обеспечивает блочную ключевую перестановку. Эти типы шифров упоминаются часто как ключевые шифры перестановки столбцов.

Предположим, что Алиса снова зашифровывает сообщение в примере 4.25, на сей раз используя объединенный подход. Шифрование и дешифрование показано на рис. 4.21.

Первая таблица, созданная Алисой, содержит исходный текст, записанный строка за строкой. Столбцы переставлены с использованием того же самого ключа, что и в предыдущем примере. Зашифрованный текст создан с помощью чтения второй таблицы столбец за столбцом. Боб делает те же самые три шага в обратном порядке. Он считывает таблицу зашифрованного текста столбец за столбцом в первую таблицу, переставляет столбцы, а затем читает вторую таблицу строку за строкой.

Ключи

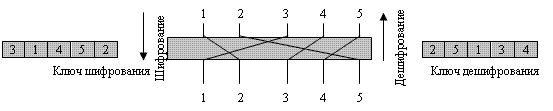
В примере 4.27 единственный ключ использовался в двух направлениях для изменения порядка следования столбцов — вниз для шифрования, вверх для дешифрования. Обычно принято создавать два ключа для этого графического представления: один для шифрования и один для дешифрования. Ключи накапливаются в таблицах, имеющих один адрес (вход) для каждого столбца. Вход содержит исходный номер столбца — номер столбца пункта назначения, указывающий его положение от номера входа. Рисунок 4.22 показывает, как эти две таблицы могут быть созданы с помощью графического представления ключа.

Ключ шифрования — (3 1 4 5 2) . Первый вход показывает, что столбец 3 (содержание) в источнике становится столбцом 1 (положение или индекс входа) в пункте назначения. Ключ дешифрования — (2 5 1 3 4) . Первый вход показывает, что столбец 2 в источнике становится столбцом 1 в пункте назначения.

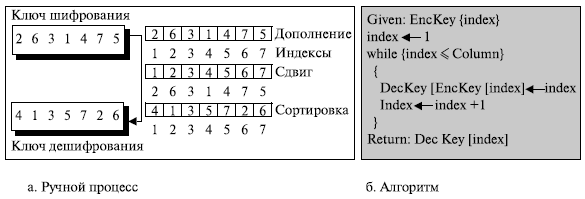
Как найти ключ дешифрования, если дан ключ шифрования или, наоборот, дан ключ дешифрации? Процесс может быть выполнен вручную за несколько шагов, как это показано на рис. 4.23. Сначала добавим индексы к таблице ключей, потом сделаем сдвиг в соответствии с полученным ключом, и, наконец, сортируем пару согласно индексу.

Использование матриц

Мы можем использовать матрицы, чтобы показать процесс шифрования/дешифрования для шифра перестановки. Исходный текст и зашифрованный текст — матрица ., представляющая числовые значения символов; ключи — квадратные матрицы размера . В матрице перестановки каждая строка или столбец имеют строго одну единицу (1) , и остальная часть значений — нули (0) . Шифрование выполняется умножением матрицы исходного текста на ключевую матрицу, чтобы получить матрицу зашифрованного текста; дешифрование выполняется умножением зашифрованного текста на инверсию ключевой матрицы, после чего получаем исходный текст.

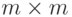
Очень интересно, что матрица дешифрования в этом случае, как и всегда, — инверсия матрицы шифрования. Однако нет никакой необходимости инвертировать матрицу — ключевая матрица шифрования может просто быть переставлена (сдвиг строк и столбцов), чтобы получить ключевую матрицу дешифрования.

Рисунок 4.24 показывает процесс шифрования. Умножение матрицы исходного текста на ключевую матрицу шифрования дает матрицу зашифрованного текста . Матричная манипуляция требует изменения символов в примере 4.27 к их числовым значениям (от 00 до 25 ). Обратите внимание, что матричное умножение обеспечивает только перестановку столбцов; чтение и запись в матрицу должны быть обеспечены остальной частью алгоритма.

Криптоанализ шифров перестановки

Шифры перестановки уязвимы к нескольким видам атак только для зашифрованного текста.

Статистическая атака

Шифр перестановки не изменяет частоту букв в зашифрованном тексте; он только переставляет буквы. Так что первая атака, которая может быть применена, — анализ частоты отдельной буквы. Этот метод может быть полезен, если длина зашифрованного текста достаточно большая. Мы такую атаку рассматривали раньше. Однако шифры перестановки не сохраняют частоту пар и триграмм. Это означает, что Ева не может использовать такие инструментальные средства. Фактически, если шифр не сохраняет частоту пар и триграмм, но сохраняет частоту отдельных букв, то вероятнее всего, что это шифр перестановки.

Атака грубой силы

Ева, чтобы расшифровать сообщение, может попробовать все возможные ключи . Однако число ключей может быть огромно 1! + 2! + 3! + … + L !, где L — длина зашифрованного текста. Лучший подход состоит в том, чтобы попробовать отгадать число столбцов. Ева знает, что число столбцов делится на L . Например, если длина шифра — 20 символов, то 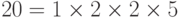. Это означает, что номером столбцов может быть комбинация этих коэффициентов (1, 2, 4, 5, 10, 20) . Однако только один столбец и только одна строка — маловероятные варианты.

Предположим, что Ева перехватила сообщение зашифрованного текста «EEMYNTAACTTKONSHITZG» . Длина сообщения L = 20 , число столбцов может быть 1, 2, 4, 5, 10 или 20 . Ева игнорирует первое значение, потому что это означает только один столбец и оно маловероятно.

a. Если число столбцов — 2 , единственные две перестановки — (1,2) и (2, 1) . Первое означает, что перестановки не было. Ева пробует вторую комбинацию. Она делит зашифрованный текст на модули по два символа «EE MY NT AA CT TK ON SH IT ZG» . Затем она пробует переставлять каждый модуль из них, получая текст «ee ym nt aa tc kt no hs ti gz» , который не имеет смысла.

b. Если номер столбцов — 4 , тогда имеется 4! = 24 перестановки. Первая перестановка (1 2 3 4) означает, что не было никакой перестановки. Ева должна попробовать остальные. После испытания всех 23 возможностей Ева находит, что никакой исходный текст при таких перестановках не имеет смысла.

c. Если число столбцов — 5 , тогда есть 5! = 120 перестановок. Первая (1 2 3 4 5) означает отсутствие перестановки. Ева должна попробовать остальные. Перестановка (2 5 13 4) приносит плоды — исходный текст «enemyattackstonightz» , который имеет смысл после удаления фиктивной буквы z и добавления пробелов.

Атака по образцу

Другая атака шифра перестановки может быть названа атакой по образцу. Зашифрованный текст, созданный с помощью ключевого шифра перестановки, имеет некоторые повторяющиеся образцы. Следующий пример показывает зашифрованный текст, относительно которого известно, что каждый символ в зашифрованном тексте в примере 4.28 получается из исходного текста по следующему правилу:

1 -й символ в зашифрованном тексте получается из 3 -го символа исходного текста. 2 -й символ в зашифрованном тексте получается из 8 -го символа исходного текста. 20 -й символ в зашифрованном тексте получается из 17 -го символа исходного текста, и так далее. У нас имеются образцы в вышеупомянутом списке. Мы имеем пять групп: (3, 8, 13, 18), (1, 6, 11, 16), (4, 9, 14, 19), (5, 10, 15, 20) и (2, 7, 12, 17) . Во всех группах разность между двумя смежными номерами — 5 . Эта регулярность может использоваться криптоаналитиком, чтобы взломать шифр. Если Ева знает или может предположить число столбцов (в этом случае оно равняется 5 ), она может преобразовать зашифрованный текст в группы по четыре символа. Перестановка групп может обеспечить ключ к нахождению исходного текста.

Шифры c двойной перестановкой

Шифры с двойной перестановкой могут затруднить работу криптоаналитика. Примером такого шифра было бы повторение дважды алгоритма, используемого для шифрования и дешифрования в примере 4.26. На каждом шаге может применяться различный ключ, но обычно ключ используется один и тот же.

Повторим пример 4.26, где использована двойная перестановка. Рисунок 4.25 показывает процесс.

Хотя криптоаналитик может еще использовать частоту появления отдельного символа для статистической атаки на зашифрованный текст, атака по образцу теперь затруднена.

Сравнив приведенный текст и результат примера 4.28, мы видим, что теперь нет повторяющихся образцов. Двойная перестановка удалила ту регулярность, что мы имели раньше.

Источник