Матричные способы представления неориентированных графов

Лабораторная работа №8

МАТРИЧНЫЕ СПОСОБЫ ПРЕДСТАВЛЕНИЯ ГРАФОВ

Целью работы является изучение матричных способов представления графов.

2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

В последнее время теория графов стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. Это проблемы проектирования интегральных схем и схем управления, исследования автоматов, логических цепей, блок-схем программ, экономики и статистики, химии и биологии, теории расписаний и дискретной оптимизации.

2.1 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Граф G задается множеством точек или вершин x₁,x₂. x_n (которое обозначается через X) и множеством линий или ребер a₁,a₂,…,a_n (которое обозначается символом А), соединяющих между собой все или часть этих точек. Таким образом, граф G полностью задается (и обозначается) парой (X, А).

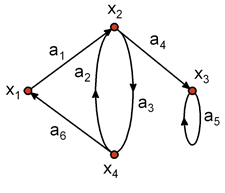
Если ребра из множества А ориентированы, что обычно показывается стрелкой, то они называются дугами, и граф с такими ребрами называется ориентированным графом (орграф) (рисунок 1(а)). Если ребра не имеют ориентации, то граф называется неориентированным (неорграф) (рисунок 1(б)). В случае когда G=(X, А) является ориентированным графом и мы хотим пренебречь направленностью дуг из множества А, то неориентированный граф, соответствующий G, будем обозначать как G=(X, А).

Если дуга обозначается упорядоченной парой, состоящей из начальной и конечной вершин (т. е. двумя концевыми вершинами дуги), ее направление предполагается заданным от первой вершины ко второй. Так, например, на рисунке 1(а) обозначение (x₁,x₂) относится к дуге a₁, а (x₂,x₁) — к дуге a₂.

Другое, употребляемое чаще описание ориентированного графа G состоит в задании множества вершин Х и соответствия Г, которое показывает, как между собой связаны вершины. Соответствие Г называется отображением множества Х в Х, а граф в этом случае обозначается парой G=(X,Г).

В случае неориентированного графа или графа, содержащего и дуги, и неориентированные ребра (см., например, графы, изображенные на рисунках 1(б) и 1(в)), предполагается, что соответствие Г задает такой эквивалентный ориентированный граф, который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Так, например, для графа, приведенного на рисунке 1(б), имеем Г(x₅)=<x₁,x₃,x₄>, Г(x₁)=<x₅> и др.

Поскольку прямое соответствие или образ вершины Г(x_i) представляет собой множество таких вершин x_jX, для которых в графе G существует дуга (x_i,x_j), то через Г -1 (x_i) естественно обозначить множество вершин x_k, для которых в G существует дуга (x_k,x_i). Такое отношение принято называть обратным соответствием или прообразом вершины. Для графа, изображенного на рисунке 1(а), имеем

Отображение Г(Г(x_i)) записывается как Г 2 (x_i). Аналогично «тройное» отображение Г(Г(Г(x_i))) записывается как Г 3 (x_i) и т. д. Для графа, показанного на рисунке 1(а), имеем:

Дугиa=(x_i,x_j), x_ix_j, имеющие общие концевые вершины, называются смежными. Две вершины x_i и x_j называются смежными, если какая-нибудь из двух дуг (x_i,x_j) и (x_j,x_i) или обе одновременно присутствуют в графе. Так, например, на рисунке 2 дуги a₁, a₁₀, a₃ и a₆ как и вершины x₅ и x₃, являются смежными, в то время как дуги a₁ и a₅ или вершины x₁ и x₄ не являются смежными.

исло дуг, которые имеют вершинуx_i своей начальной вершиной, называется полустепенью исхода вершины x_i, и, аналогично, число дуг, которые имеют x_i своей конечной вершиной, называется полустепенью захода вершины x_i.

Очевидно, что сумма полустепеней захода всех вершин графа, а также сумма полустепеней исхода всех вершин равны общему числу дуг графа G, т. е.

, (1)

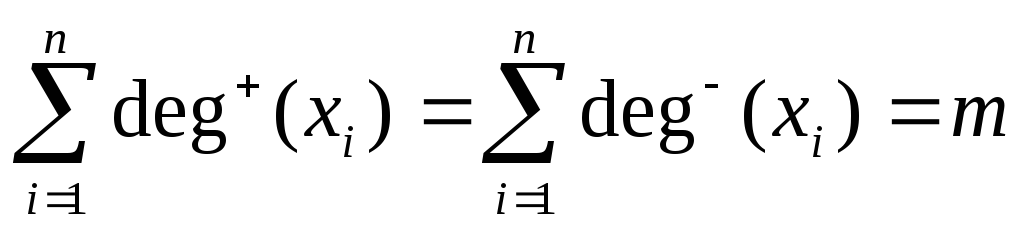
где n — число вершин и m — число дуг графа G.

Петлей называется дуга, начальная и конечная вершины которой совпадают. На рисунке 3, например, дуги a₃ и a₁₀ являются петлями.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Графы и способы их представления

Способы описания графов

Теоретико-множественное представление графов

Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.

где X = – множество вершин графа , A = i>, i = 1, 2, . 5 – множество дуг графа , причем a₁ = (F, B) , a₂ = (F, D) , a₃ = (B, E) , a₄ = (E, C) , a₅ = (C, D) .

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г , которое показывает, как между собой связаны вершины.

Соответствием Г называется отображение множества Х в Х , а граф в этом случае обозначается парой G = (X, Г) .

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i , т. е. .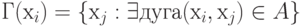

Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:

Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф , который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х₂) = < х₁, х₃, х₅ >, Г(х₄) =< х₃, х₅> и т. д.

Матричное представление графов

Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций .

Матрица смежности – это квадратная матрица размерностью n x n , (где n – число вершин графа ), однозначно представляющая его структуру.

A = ij>, i, j = 1, 2, . n , а каждый элемент матрицы определяется следующим образом:

a_ij = 1 , если дуга (х_i, х_j) ,

Если элемент на диагонали (i=j) равен единице, значит, вершина i имеет петлю.

Матрица инциденций представляет собой прямоугольную матрицу размером n x m , где n – количество вершин графа , а m – количество дуг графа . Обозначается матрица инциденций B = ij>, i = 1, 2, . n, j = 1, 2, . m .

Каждый элемент матрицы определяется следующим образом:

b_ij = 1 , если х_i является начальной вершиной дуги a_j ,

b_ij = –1 , если х_i является конечной вершиной дуги a_j ,

b_ij = 0 , если х_i не является концевой вершиной дуги a_j или если a_j является петлей.

Таким образом, нулевой столбец j в матрице инциденций свидетельствует о том, что дуга a_j яляется петлей.

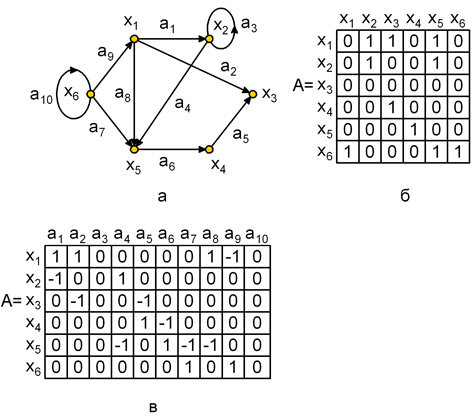
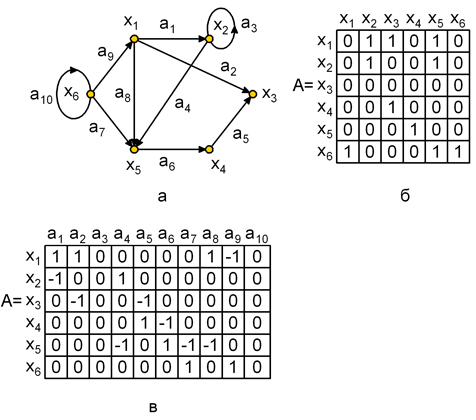
На рис. 1.5, а,б приведен граф и его матрица смежности , по которой можно найти характеристики вершин. Так сумма элементов i -ой строки матрицы дает полустепень исхода вершины х_i , а сумма элементов i -го столбца дает полустепень захода вершины х_i . По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i -ю строку матрицы. Если элемент a_ij=1 , то элемент графа х_j входит в отображение Г(х_i) . Например, во 2-й строке матрицы А ( рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х₂) = < х₂, х₅> .

Для графа на рис. 1.5,а матрица инциденций приведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа , матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.

Источник

Матричное представление графов

Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций.

Матрица смежности – это квадратная матрица размерностью n x n, (где n – число вершин графа), однозначно представляющая его структуру.

A = ij>, i, j = 1, 2, . n, а каждый элемент матрицы определяется следующим образом:

Матрица инциденций представляет собой прямоугольную матрицу размером n x m, где n – количество вершин графа, а m – количество дуг графа. Обозначается матрица инциденций B = = ij>, i = 1, 2, . n, j = 1, 2, . m.

Каждый элемент матрицы определяется следующим образом:

b_ij = 1, если х_i является начальной вершиной дуги a_j,

b_ij = –1, если х_i является конечной вершиной дуги a_j,

b_ij = 0, если х_i не является концевой вершиной дуги a_j или если a_j является петлей.

Рис.2. Орграф и его матричное представление: а – орграф; б – матрица смежности; в – матрица инциденций

На рис.2, а,б приведен граф и его матрица смежности, по которой можно найти характеристики вершин. Так сумма элементов i-ой строки матрицы дает полустепень исхода вершины х_i, а сумма элементов i-го столбца дает полустепень захода вершины х_i. По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i-ю строку матрицы. Если элемент a_ij=1, то элемент графа х_j входит в отображение Г(х_i). Например, в 2-й строке матрицы А (рис.2,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х₂) = < х₂, х₅>.

Для графа на рис.2,а матрица инциденций приведена на рис.4,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа, матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.

Источник

Графы и способы их представления

Способы описания графов

Теоретико-множественное представление графов

Граф описывается перечислением множества вершин и дуг. Примеры описания приведены для орграфов на рис. 1.3 и рис. 1.4.

где X = – множество вершин графа , A = i>, i = 1, 2, . 5 – множество дуг графа , причем a₁ = (F, B) , a₂ = (F, D) , a₃ = (B, E) , a₄ = (E, C) , a₅ = (C, D) .

Задание графов соответствием

Описание графов состоит в задании множества вершин Х и соответствия Г , которое показывает, как между собой связаны вершины.

Соответствием Г называется отображение множества Х в Х , а граф в этом случае обозначается парой G = (X, Г) .

Отображением вершины х_i — Г(х_i) является множество вершин, в которые существуют дуги из вершины х_i , т. е. .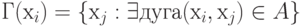

Так для орграфа на рис. 1.3 описание заданием множества вершин и соответствия выглядит следующим образом:

Для неориентированного или смешанного графов предполагается, что соответствие Г задает такой эквивалентный ориентированный граф , который получается из исходного графа заменой каждого неориентированного ребра двумя противоположно направленными дугами, соединяющими те же самые вершины. Например, для графа на рис. 1.2,б Г(х₂) = < х₁, х₃, х₅ >, Г(х₄) =< х₃, х₅> и т. д.

Матричное представление графов

Для обработки на ЭВМ графы удобно представлять в виде матриц смежности и инциденций .

Матрица смежности – это квадратная матрица размерностью n x n , (где n – число вершин графа ), однозначно представляющая его структуру.

A = ij>, i, j = 1, 2, . n , а каждый элемент матрицы определяется следующим образом:

a_ij = 1 , если дуга (х_i, х_j) ,

Если элемент на диагонали (i=j) равен единице, значит, вершина i имеет петлю.

Матрица инциденций представляет собой прямоугольную матрицу размером n x m , где n – количество вершин графа , а m – количество дуг графа . Обозначается матрица инциденций B = ij>, i = 1, 2, . n, j = 1, 2, . m .

Каждый элемент матрицы определяется следующим образом:

b_ij = 1 , если х_i является начальной вершиной дуги a_j ,

b_ij = –1 , если х_i является конечной вершиной дуги a_j ,

b_ij = 0 , если х_i не является концевой вершиной дуги a_j или если a_j является петлей.

Таким образом, нулевой столбец j в матрице инциденций свидетельствует о том, что дуга a_j яляется петлей.

На рис. 1.5, а,б приведен граф и его матрица смежности , по которой можно найти характеристики вершин. Так сумма элементов i -ой строки матрицы дает полустепень исхода вершины х_i , а сумма элементов i -го столбца дает полустепень захода вершины х_i . По матрице смежности можно найти прямые и обратные отображения. Рассмотрим i -ю строку матрицы. Если элемент a_ij=1 , то элемент графа х_j входит в отображение Г(х_i) . Например, во 2-й строке матрицы А ( рис. 1.5,б) единицы стоят в 2-м и 5-м столбцах, следовательно, Г(х₂) = < х₂, х₅> .

Для графа на рис. 1.5,а матрица инциденций приведена на рис. 1.5,в. Поскольку каждая дуга инцидентна двум различным вершинам, за исключением того случая, когда дуга образует петлю, то каждый столбец либо содержит один элемент равный 1 и один – равный – 1, либо все элементы столбца равны 0.

Для неориентированного графа , матрица инциденций определяется так же, за исключением того, что все элементы, равные –1, заменяются на 1.

Источник