Матлаб способы задания массива

Наборы чисел в программировании принято называть массивами. Всему массиву присваивается одно имя, а доступ к отдельным элементам массива осуществляется по целочисленному индексу, то есть номеру элемента в массиве. Массивы бывают одномерными, когда используется единственный индекс (номер), а могут быть и многомерными (в частности — двумерными).

Сначала рассмотрим одномерные массивы. Это линейные наборы чисел (элементов), в которых позиция каждого элемента задаётся единственным числом — его номером. Можно говорить о первом элементе массива, о втором и т.д.

Для задания одномерного массива, состоящего из нескольких чисел (вещественных или комплексных), используется операция конкатенации, обозначаемая с помощью квадратных скобок — [] . Например, следующее выражение

формирует переменную с именем a1 , являющуюся одномерным массивом из трёх элементов (вещественных чисел). Объединяемые в массив элементы должны отделяться друг от друга либо пробелом, либо запятой. Так что выражение

абсолютно идентично предыдущему.

Для доступа к индивидуальному элементу одномерного массива нужно после его имени указать в круглых скобках индекс (номер) этого элемента. Например, третий элемент массива a1 обозначается как a1(3) , первый элемент — как a1(1) , второй элемент — как a1(2) .

Если требуется изменить третий элемент уже сформированного выше операцией конкатенации массива a1 , то можно применить операцию присваивания:

Пусть, к примеру, второй элемент массива a1 должен стать равным среднему арифметическому первого и третьего элементов. Для этого выполняем следующее действие:

Количество элементов в одномерном массиве всегда можно узнать с помощью функции length :

При попытке чтения несуществующего элемента (напрмер, четвёртого элемента массива a1 ) в командном окне MATLABа появляется сообщение об ошибке:

В этом сообщении утверждается, что индекс превысил размер массива.

В то же время запись несуществующего элемента вполне допустима — она означает добавление нового элемента к уже существующему массиву:

Применяя к массиву a1 функцию length , находим, что количество элементов в этом массиве возросло до четырёх:

То же самое действие — «удлинение массива a1 » ,можно выполнить и с помощью операции конкатенации:

Здесь операндами операции конкатенации являются массив a1 , состоящий из трёх элементов, и добавляемый к нему четвёртый элемент, равный 7 .

Теперь создадим ещё один одномерный массив a2 , причём для его создания не будем использовать операцию конкатенации (как мы поступили выше). Вместо этого будем прописывать каждый элемент создаваемого массива по-отдельности:

a2(1) = 67
a2(2) = 7.8
a2(3) = 0.017

Из двух существующих массивов — массива a1 с четырьмя элементами и массива a2 с тремя элементами, можно одной (групповой) операцией конкатенации создать одномерный массив b из семи элементов:

Массивы могут состоять не только из вещественных чисел. Выражение

d = [ 1+2i, 2+3i, 3-7i ]

формирует одномерный массив d комплексных чисел. Разделителем элементов формируемого одномерного массива может быть либо пробел, либо запятая. При использовании выражений и комплексных чисел использование запятой предпочтительнее.

Теперь рассмотрим двумерные массивы, которые можно трактовать как набор чисел, упорядоченный в виде прямоугольной таблицы, когда для доступа к индивидуальному элементу используется два индекса — номер строки и номер столбца (на пересечении которых и стоит выбранный элемент).

Двумерный массив характеризуется количеством строк и количеством столбцов. Составим массив a3 , состоящий из двух столбцов и трёх строк:

Из этого рисунка хорошо видно, что в качестве разделителя строк в формируемом с помощью операции конкатенации двумерном массиве служит точка с запятой.

Как и в случае одномерных массивов двумерный массив можно создать, индивидуально прописывая его элементы:

a3(1,1) = 1
a3(1,2) = 2
a3(2,1) = 3
a3(2,2) = 4
a3(3,1) = 5
a3(3,2) = 6

Для доступа к отдельным элементам двумерного массива используется выражение с круглыми скобками, в которых через запятую перечисляются его индексы. Первым указывается номер строки, вторым — номер столбца.

Система MATLAB может работать и с массивами больших размерностей. Они будут рассматриваться позже в следующем разделе.

Вернёмся к двумерным массивам, которые в математике принято называть матрицами. Любая строка матрицы является одномерным массивом, и любой столбец матрицы также является одномерным массивом. Однако есть некоторая разница в упорядочении их элементов с точки зрения матриц: элементы первого одномерного массива упорядочены вдоль строк матрицы (горизонтально), а элементы второго — вдоль столбцов (вертикально). Если явно учитывать в понятии одномерного массива эту разницу, то тогда массивы первого типа называют вектор-строками, а второго типа — вектор-столбцами. В этом случае также можно считать, что вектор-строки являются частным случаем матрицы с количеством строк, равным единице, а вектор-столбцы являются частным случаем матрицы с количеством столбцов, равным единице.

В системе MATLAB все одномерные массивы трактуются либо как вектор-строки, либо как вектор-столбцы. До сих пор мы вводили только вектор-строки. Следующее выражение, использующее операцию конкатенации, задаёт вектор-столбец

состоящий из трёх строк, так как точка с запятой в операции конкатенации означает переход на новую строку.

Для массива a4 функция length(a4) возвращает число 3 , так как действительно этот массив состоит из трёх элементов. Функция length не различает вектор-строки и вектор-столбцы.

Если попросить систему MATLAB показать значение переменной a4 , то мы увидим следующую картину:

То есть MATLAB распознаёт «геометрию» этого одномерного массива и наглядно отображает его, располагая элементы для показа в своём окне вертикально.

Чтобы отразить правильно геометрию вектор-столбцов и вектор-строк, а также узнать размеры двумерного массива в обоих направлениях, используют функцию size . Для двумерного массива a3 получается следующий результат:

причём первым показывается число строк, а вторым — число столбцов.

Применяем эту же функцию к одномерным массивам. Вот, что из этого получается для вектор-строки a2

состоящего из одной строки и трёх столбцов. Для вектор-столбца a4 , состоящего из трёх строк и одного столбца, имеем следующий результат применения функции size :

Наконец, попробуем применить эту функцию к переменной, состоящей из единственного числового значения, то есть к скаляру:

var1 = 5
size(var1)
ans =
1 1

Отсюда видно, что система MATLAB трактует даже по-существу скалярные величины как массивы с размером 1×1. Это ровным счётом ничего не меняет для пользователя, так как он может не обращать на это никакого внимания. MATLAB переходит от скаляров к массивам прозрачно, не требуя от пользователя дополнительных действий.

Итак, всё, с чем работает MATLAB, является массивами различной размерности. Все массивы из текущего сеанса работы (текущего Рабочего пространства) можно просмотреть

с точки зрения их структуры с помощью команды whos .

Источник

Документация

Многомерный массив в MATLAB® является массивом больше чем с двумя размерностями. В матрице эти две размерности представлены строками и столбцами.

Каждый элемент задан двумя индексами, индексом строки и индексом столбца. Многомерные массивы являются расширением 2D матриц и используют дополнительные индексы для индексации. Трехмерный массив, например, использует три индекса. Первые два точно так же, как матрица, но третья размерность представляет страницы или листы элементов.

Создание многомерных массивов

Можно создать многомерный массив путем создания 2D матрицы сначала, и затем расширения его. Например, сначала задайте 3х3 матрицу как первую страницу в трехмерном массиве.

Теперь добавьте вторую страницу. Для этого присвойте другую 3х3 матрицу значению индекса 2 в третьей размерности. Синтаксис A(. 2) использует двоеточие в первых и вторых измерениях, чтобы включать все строки и все столбцы с правой стороны присвоения.

cat функция может быть полезным инструментом для создания многомерных массивов. Например, создайте новый трехмерный массив B путем конкатенации A с третьей страницей. Первый аргумент указывает который размерность конкатенировать вперед.

Иначе быстро расширить многомерный массив путем присвоения одного элемента целой странице. Например, добавьте четвертую страницу в B это содержит все нули.

Доступ к элементам

Для доступа к элементам в многомерном массиве используйте целочисленные индексы, так же как для векторов и матриц. Например, найдите 1,2,2 элемента A , который находится в первой строке, втором столбце и второй странице A .

Используйте вектор индекса [1 3] во втором измерении, чтобы получить доступ только к первым и последним столбцам каждой страницы A .

Чтобы найти вторые и третьи строки каждой страницы, используйте оператор двоеточия, чтобы создать ваш вектор индекса.

Управление массивами

Элементы многомерных массивов могут быть перемещены во многих отношениях, похожие на векторы и матрицы. reshape перестановка , и squeeze полезные функции для реорганизации элементов. Рассмотрите трехмерный массив с двумя страницами.

Изменение размерность многомерного массива может быть полезно для выполнения определенных операций или визуализации данных. Используйте reshape функционируйте, чтобы перестроить элементы трехмерного массива в 6 5 матрица.

reshape действует по столбцам, создавая новую матрицу путем взятия последовательных элементов вниз каждый столбец A , Начиная с первой страницы, затем перемещающейся во вторую страницу.

Сочетания используются, чтобы перестроить порядок размерностей массива. Считайте трехмерный массив M .

Используйте permute функционируйте, чтобы обменяться индексами строки и столбца на каждой странице путем определения порядка размерностей во втором аргументе. Исходные строки M теперь столбцы, и столбцы являются теперь строками.

Точно так же обменяйтесь строкой и индексами страницы M .

При работе с многомерными массивами вы можете столкнуться с тем, который имеет ненужную размерность длины 1. squeeze функция выполняет другой тип манипуляции, которая устраняет размерности длины 1. Например, используйте repmat функция, чтобы создать 2 3 массивом 1 на 4, элементы которого — каждый 5, и чья третья размерность имеет длину 1.

Используйте squeeze функция, чтобы удалить третью размерность, приводящую к трехмерному массиву.

Открытый пример

У вас есть модифицированная версия этого примера. Вы хотите открыть этот пример со своими редактированиями?

Документация MATLAB

Поддержка

1. Если смысл перевода понятен, то лучше оставьте как есть и не придирайтесь к словам, синонимам и тому подобному. О вкусах не спорим.

2. Не дополняйте перевод комментариями “от себя”. В исправлении не должно появляться дополнительных смыслов и комментариев, отсутствующих в оригинале. Такие правки не получится интегрировать в алгоритме автоматического перевода.

3. Сохраняйте структуру оригинального текста — например, не разбивайте одно предложение на два.

4. Не имеет смысла однотипное исправление перевода какого-то термина во всех предложениях. Исправляйте только в одном месте. Когда Вашу правку одобрят, это исправление будет алгоритмически распространено и на другие части документации.

5. По иным вопросам, например если надо исправить заблокированное для перевода слово, обратитесь к редакторам через форму технической поддержки.

Источник

Различные способы задания массивов.

Матрицы

Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы. Если у матрицы количество строк m совпадает с количеством столбцов n, то такая матрица называется квадратной, а числоm=nназывается размером квадратной матрицы или её порядком.

Примеры. Задание матрицы в matlab:

Основной способ: с помощью оператора квадратные скобки: [ ]

Матрица из единиц:ones(…)

Матрица из нулей:zeros(…)

Единичная матрица:eye(…) – на главной диагонали стоят единицы, на остальных местах нули.

Векторы

Матрица из одной строки называется вектор-строкой, из одного столбца – вектор-столбцом, такие матрицы мы будем называть просто векторами.

Упражнение 4.. Различные способы задания векторов.

1) Задать вектор-строку 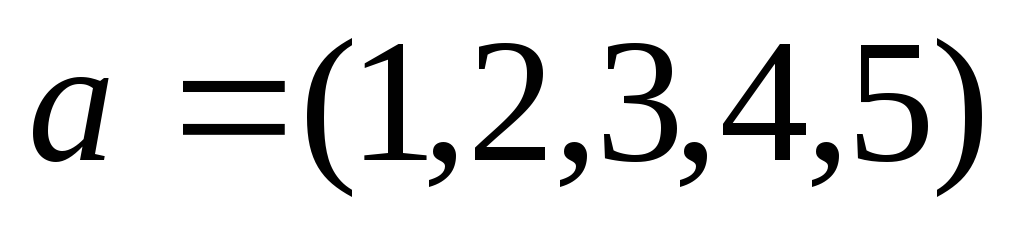с помощью

a) ввода чиселcпробелами;

b) ввода чисел с запятыми;

c) стандартной функциейhorzcat(, , , )

d) двоеточия «:» с шагом можно задать те же числа от 1 до 6 с шагом 1

2)Задать вектор-столбец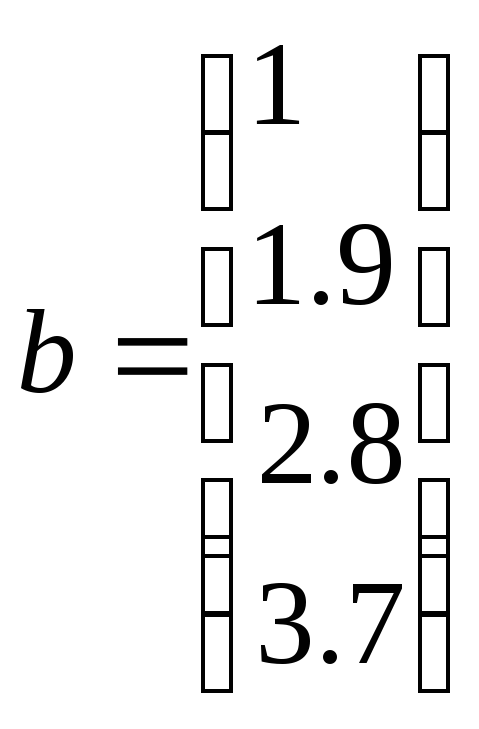с помощью

a) точки запятой «;» ;

b) транспонировав вектор-строку, с помощью символа«’» — одинарная кавычка (буква э в латинском регистре)

с) стандартной функцией vertcat(, , ,)

d) двоеточия «:» с шагом и транспонирования«’».

1. Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:

>> v1 = [1; 2]; v2 = [3; 4; 5]; v = [v1; v2]

2. Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:

>> w1 = [1 2]; w2 = [3 4 5]; w = [w1 w2]

Арифметические операции над массивами

Основные математические функции

Напомним, что все данные в системе MATLAB– массивы. Все операции над массивами реализуются посредством функций.С каждой из традиционных операций (с умножением, делением и возведением в степень) связаны по две функции «*», «.*», «/», «./», «^», «.^». «Список этих функций приведен в табл. 3 см. вhelpMATLABраздел «ArithmeticOperators.» а также. Л.1 стр. 27). Серым цветом выделены функции, которыми будем пользоваться по мере изучения соответствующих понятий в курсе линейной алгебры.

Покомпонентное сложение числовых массивов одинаковой размерности.

Добавление скалярной величины к каждому элементу массива.

Покомпонентное вычитание числовых массивов одинаковой размерности.

Вычитание скалярной величины от каждого элемента массива.

Умножение скаляра на скаляр

Покомпонентное умножение всех элементов массива на скаляр.

Матричное умножение. Умножение матриц в соответствии с правилами линейной алгебры (условие выполнения: число столбцов первого сомножителя должно быть равно числу строк второго сомножителя)

Покомпонентное умножение массивов одинаковой размерности

Деление скаляра на скаляр.

Покомпонентное деление всех элементов массива на скаляр.

Правое матричное деление.

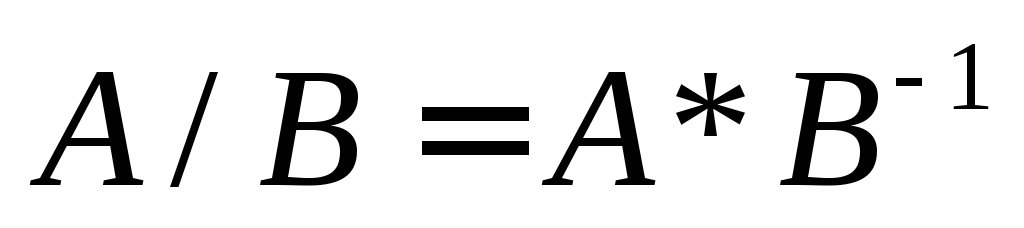
(A и B – квадратные матрицы одного порядка).

Правое покомпонентное деление элементов массивов одинаковой размерности.

Возведение скаляра в степень.

Матричное возведение в степень, равносильно умножению матрицы на себя.

Поэлементное возведение элементов матрицы степень.

Эрмитово сопряжение – одновременное: комплексное сопряжение и транспонирование:

Ни правым «/», ни левым «\» делением в смысле матричного деления мы пользоваться непосредственно не будем.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Матлаб способы задания массива