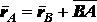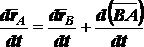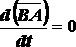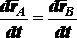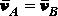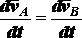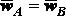Материальная точка способы задания движения материальной точки

Способы задания движения материальной точки скорость, ускорение

Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, как уже отмечалось, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.

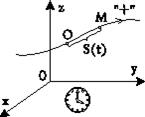
1. Естественный способ. Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать (рис. 1):

а) траекторию движения (относительно какой-либо системы координат);

б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;

в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);

г) начало отсчета времени t;

д) функцию S(t), которая называется законом движения**) точки.

2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:

а) системы координат (не обязательно декартовой) q1, q2, q3;

б) начало отсчета времени t;

в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).

Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.

3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку (рис. 2). В этом случае для описания движения необходимо задать:

а) начало отсчета радиус-вектора r;

б) начало отсчета времени t;

в) закон движения точки r(t).

Ускорение точки. , [м/сек2]. Проекции уск.-я: и т.д. Модуль уск.-я: , направляющ. косинусы: , и т.д.

При задании движения в полярных координатах: проекции ускорения на радиальное направление , поперечное направление , модуль ускорения . При естественным сп. задания движения полное ускорение раскладывают на нормальное и касательное (тангенциальное) ускорения: . Модуль нормального ускорения: , r – радиус кривизны траектории, нормальное ускорение направлено по нормали к траектории (^ к касательной) всегда к центру кривизны, т.е. в сторону вогнутости. Нормальное ускорение характеризует изменение скорости по направлению. Модуль касательного ускорения , направлено по касательной к траектории, либо в сторону скорости, либо в обратную. Касательное ускорение характеризует изменение скорости по величине. При ускоренном движ-ии направление касат. уск. и скорости совпадают, при замедленном – противоположно. ^ , Þ . Вектор ускорения лежит в соприкасающейся плоскости Þ его проекция на бинормаль равна 0 (главная нормаль лежит в соприкасающейся плоскости, т.е. в плоскости плоской кривой, бинормаль – ^ к главной нормали и касательной). Частные случаи движения точки:

1) Прямолинейное: радиус кривизны r= ¥ (бесконечно большой) Þ аn=0, a=at.

2) Равномерное криволинейное движ-ие: v=const Þ at=0, a=an. Уск. появляется только за счет изменения направления скорости. Закон движ-ия: s=s0+v×t, при s0=0 v=s/t.

3) Равномерное прямолинейное движ-ие: а=at=an=0. Единственное движ-ие, где а=0.

4) Равнопеременное криволинейное движ-ие: at=const, v=v0+at×t, . При равноуск. движении знаки у at и v одинаковы, при равнозамедленном – разные.

13)Поступательным движением твердого тела называется такое его движение, при котором любая прямая, проведенная в теле, остается параллельной своему первоначальному положению во все время движения.

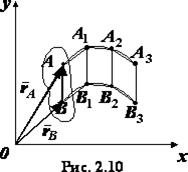
Теорема. При поступательном движении твердого тела все его точки движутся по одинаковым и параллельным траекториям и имеют в каждый данный момент времени равные по модулю и направлению скорости и ускорения.

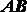
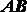
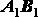
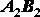
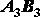
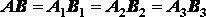
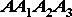
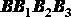
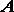
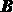
Доказательство. Для доказательства теоремы рассмотрим движение отрезка прямой , проведенного в теле, совершающем поступательное движение (рис. 2.10). Из определения поступательного движения следует, что в каждый данный момент времени отрезок , занимающий последовательно положения , , и т.д., остается параллельным своему первоначальному положению. Учитывая это и то что , делаем вывод, что ломаные линии и параллельны и при наложении совпадут всеми своими точками. При бесконечном уменьшении промежутков времени между рассматриваемыми положениями отрезка мы видим, что точка и точка описывают одинаковые кривые, т. е. кривые, совпадающие при наложении.

Для доказательства второй части теоремы заметим, что

Возьмем производные по времени от левой и правой частей

Так как , 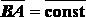то .

Разобранная теорема позволяет сделать вывод, что поступательное движение твердого тела вполне определяется движением какой-либо одной его точки

Источник

iSopromat.ru

Рассмотрим три существующих способа задания движения материальной точки: координатный, векторный и естественный.

Чтобы иметь возможность определить параметры движения точки необходимо задать закон ее движения.

В зависимости от известных величин и поставленной задачи могут быть использованы следующие способы задания движения точки: векторный, координатный и естественный.

Векторный

При векторном способе задания движения положение точки определяется радиус-вектором, проведенным из неподвижной точки в выбранной системе отсчета.

Координатный

При координатном способе задания движения задаются координаты точки как функции времени:

Это параметрические уравнения траектории движущейся точки, в которых роль параметра играет время t. Чтобы записать ее уравнение в явной форме, надо исключить из них t.

Естественный

При естественном способе задания движения задаются траектория точки, начало отсчета на траектории с указанием положительного направления отсчета, закон изменения дуговой координаты: s=s(t). Этим способом удобно пользоваться, если траектория точки заранее известна.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

Материальная точка способы задания движения материальной точки

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Способы задания движения материальной точки

Точка движется в пространстве по некоторой линии, или траектории.

— Естественный способ — движение точки задано, если известны:

1) траектория точки;

2) зависимость изменения длины дуги от времени: ОМ =S =f(t) (эта зависимость называется

уравнением движения материальной точки);

3) начало движения;

4) начало отсчета;

5) направление отсчета.

— Векторный способ Положение точки в пространстве определяется радиусом-вектором r-, проведенным из некоторого неподвижного центра в данную точку М.

Положение точки в пространстве в этом случае будет определяться геометрическим местом концов векторов r-,.

— Координатный способ задания движения должны быть известны зависимости, по которым можно определить, как со временем изменяются координаты точки в пространстве:

x =f1(t);y =f2(t);z =f3(t) — уравнениями движения точки в декартовых координатах, с их помощью для каждого момента времени можно определить положение точки в пространстве.

Если точка движется на плоскости, то ее положение описывается двумя уравнениями:

если точка движется по прямой, то достаточно только одного уравнения:

Скорость точки характеризует быстроту и направление движения точки. При векторном способе задания движения положение точки в каждый момент времени определяется радиусом-вектором r— =r-(t).

Динамика — раздел механики, в котором изучается движение материальных тел под действием приложенных к ним сил.В основе динамики лежат законы И.Ньютона.

Первый закон — закон инерции, установленный Галилеем, гласит: материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не изменит это состояние.

Второй закон— основной закон динамики— устанавливает связь между ускорением a-, массой m материальной точки М и силой F (рис. 1.51, а):ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление.

Масса является мерой инертности материальных тел в их поступательном движении. Запишем основной закон динамики в скалярном виде, проецируя векторные величины, входящие в равенство, на оси координат:

Третий закон: всякому действию соответствует равное и противоположно направленное противодействие.

Этот закон устанавливает, что при взаимодействии двух тел, в каком бы кинематическом состоянии они не находились, силы, приложенные к каждому из них, равны по модулю и направлены по одной прямой в противоположные стороны.

Четвертый закон: несколько одновременно действующих сил сообщают точке такое ускорение, какое сообщала бы одна сила, равная их геометрической сумме.

Основной закон динамики можно записать в скалярном виде, спроецировав векторы либо на декартовы, либо на естественные оси координат.

Механической системой называют мысленно выделенную совокупность материальных точек, взаимодействующих между собой. Механическую систему иногда называют материальной системой или системой материальных точек.

Существуют системы материальных точек:

— свободных (например, Солнечная система)

— несвободных (их движения ограничены связями). Пример: любой механизм или машина. Все силы, действующие на систему несвободных точек, подразделяют на задаваемые (активные) силы и реакции связей (пассивные силы).

Силы, действующие на точки любой механической системы, делят на:

— внешние — действующие на точки системы со стороны материальных точек, не входящих в состав данной системы.

— внутренние — силы взаимодействия между материальными точками данной механической системы (силы упругости, действующие между частицами упругого тела, принятого за механическую систему).

Одна и та же сила может быть как внешней, так и внутренней в зависимости от того, какая механическая система рассматривается. Например, реакции подшипников вала являются внешними силами по отношению к валу. Эти же реакции можно отнести к внутренним силам, если рассматривать всю установку вместе с машиной.

Таким образом, любая сила может быть внешней или внутренней, в то же время она может быть задаваемой или реакцией связи. Движение точек системы зависит как от внешних, так и от внутренних сил.

По закону равенства действия и противодействия каждой внутренней силе соответствует другая внутренняя сила, равная ей по модулю и противоположная по направлению.

Виды движения твердого тела

Дата добавления: 2018-04-05 ; просмотров: 1040 ; Мы поможем в написании вашей работы!

Источник