Математика как способ познания мира
Беседа 1. Математика как метод и язык познания окружающего мира
Как устроен окружающий мир? Каковы законы развития природы? Как можно их использовать для блага людей? Можно ли подчинить некоторые явления природы человеку? Каким образом можно преобразовать мир? Подобного рода вопросы волновали и волнуют человечество с незапамятных времен. Гениальные умы строили гипотезы, доказывали одни из них и опровергали другие, спорили. Преодолевая заблуждения, люди шли к истине. Как ее познать? Где тот волшебный фонарь, который освещает путь к истине?
В течение многих веков для изучения явлений окружающего мира создавались разные науки, каждая из которых изучала определенные стороны этого мира, определенную область явлений или процессов в природе и обществе.
В любой науке в той или иной степени приходится изучать не только качественные особенности предметов, явлений или процессов, но и пространственные и количественные особенности.
Для изучения количественных и пространственных особенностей различных предметов, явлений или процессов в разных науках надо было разработать общий метод изучения этих особенностей. Вот этот всеобщий метод и разрабатывается в математике. Это предельно четко сформулировал Ф. Энгельс (1820-1895) в своем определении математической науки.
Он указал, что математика занимается изучением особой стороны любых предметов, явлений или процессов окружающего мира, а именно количественных отношений и пространственных форм. Следовательно, когда в той или иной науке исследуют тот или иной объект (явление, процесс), то, рассматривая количественные отношения или пространственные формы в этих объектах (а без такого рассмотрения изучение будет совершенно неполным и малозначимым), с необходимостью используют математические методы, математический аппарат.
Каждая наука, пользуясь математическими методами, строит определенную схему-представление об изучаемом предмете (явлении или процессе). Эта схема-представление в виде какой-то формулы, уравнения или в виде геометрического образа называется математической моделью изучаемого объекта (предмета, явления, процесса). Затем с помощью этой модели делают логические выводы, справедливость которых проверяют на практике, в эксперименте. Если результаты практической проверки подтверждают справедливость этих выводов-следствий построенной модели, то это служит свидетельством правильности модели; если же хотя бы один из выводов-следствий не подтверждается на практике, то ученые уточняют разработанную модель или же вовсе отказываются от нее и строят новую модель изучаемого объекта.
Движение к истине, к познанию подлинных законов природы и общества идет через построение все более точных, более правильных математических моделей изучаемого предмета (явлений, процессов).
Таким образом, математика занимается разработкой методов построения и методов изучения конкретных математических моделей для различных наук. Для этого она строит математический аппарат, разрабатывает математические понятия. Например, числовые системы (системы натуральных, рациональных и действительных чисел), которые вы изучаете в школе, являются примером такого математического аппарата, с помощью которого в самых различных науках строятся математические модели той стороны изучаемых объектов (предметов, явлений), которая связана с измерением величин. Функция представляет собой другой пример математического аппарата, с помощью которого в различных науках строятся конкретные математические модели изучаемых явлений или процессов и т. д.
При построении математических моделей используется особый математический язык (совокупность символов и обозначений, принятых в математике).
Именно поэтому говорят, что математика представляет собой всеобщий язык науки. Эту сторону математики уже давно выделяли. Так, например, еще Галилей почти 400 лет тому назад писал: «Философия написана в грандиозной книге — Вселенной, которая открыта нашему пристальному взгляду. Но понять эту книгу может лишь тот, кто научился понимать ее язык и знаки, которыми она изложена. Написана же она на языке математики. » * .
* ( Во время Галилея всю науку называли философией.)
Математический язык, в отличие от языка, на котором мы говорим в обыденной жизни, является очень удобным для краткого и точного описания различных понятий и зависимостей многих наук: физики, химии, биологии, а также, казалось бы, далеких от математики, как экономика, лингвистика (наука о языке), психология и т. д. Математический язык дает возможность не только описывать те или иные зависимости, характеризующие конкретные явления или процессы, но и осуществлять проверку этих зависимостей путем сопоставления результатов вычислений с результатами, найденными опытным путем. Формулировка зависимостей той или иной науки на математическом языке позволяет также делать различного рода предсказания и новые открытия чисто математическим путем. Так, например, была открыта планета Нептун с помощью одних вычислений, и лишь затем ее обнаружили с помощью телескопов в указанном Леверье в 1845 г. месте небесного свода.
Сейчас уже всеми признается справедливость замечания Карла Маркса, что любая наука только тогда достигает совершенства, когда она пользуется математикой.
Особенностью математического метода изучения явлений окружающего мира является то, что он позволяет избежать ошибок, присущих нашему восприятию, и увидеть то, что недоступно даже воображению. Приведем один пример.
Как вы думаете, где больше точек: в отрезке длиной 1 см или в отрезке длиной 3 см? Наше непосредственное восприятие подсказывает нам, что во втором отрезке точек больше, чем в первом. Между тем еще давно было показано, что это не-верно. Вот как следует рассуждать.
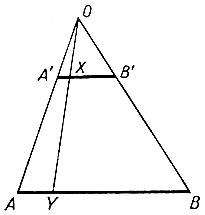
Рис. 1
Построим отрезки а=3 см и а ‘ = см так, чтобы они были параллельны друг другу. Затем через точки А и А ‘ , а также через точки В и В ‘ проводим лучи до взаимного пересечения в точке О (рис. 1). Будем считать, что точке А ‘ соответствует точка А, а точке В ‘ — точка В. Возьмем на отрезке А ‘ В ‘ произвольную точку X и проведем через нее из точки О луч, он пересечет отрезок АВ в точке Y. Будем считать точку Y соответствующей точке X. Таким образом мы сумеем каждой точке X отрезка А ‘ В ‘ поставить в соответствие единственную точку Y отрезка АВ. При этом верно и обратное, а именно каждой точке Y отрезка АВ соответствует одна и только одна точка X отрезка А ‘ В ‘ . Это и означает, что множество точек на этих двух отрезках одинаковое.
Данный пример показывает, как прав гениальный математик Леонард Эйлер (1707-1783), который писал:
«Именно математика в первую очередь защищает нас от обмана чувств и учит, что одно дело — как на самом деле устроены предметы, воспринимаемые чувствами, другое дело — какими они кажутся; эта наука дает надежнейшие правила; кто им следует — тому не опасен обман чувств».
Источник
Математика как способ познания мира
Наградной документ — бесплатно!
Записывайся на интересные курсы
или размещай свои!
Автор: Гусенкова Елена Станиславовна Должность: преподаватель Город/Населенный пункт: Самарская область, г. Жигулевск Дата публикации: 12.03.2020
Математика — язык познания мира
Математика из покрытой ореолом таинственности науки превращается в обычный инструмент исследования, потребность в использовании которого ощущает все большее число специалистов в разных областях знания.
Математика была, есть и будет элементом общей культуры. Но если в этом качестве раньше она была уделом небольшого числа посвященных людей, то теперь, объективные тенденции научно-технического прогресса делают математические методы достоянием широкого круга людей, занятых в самых различных сферах науки и техники.
С чем связана наблюдаемая в последнее время интенсивная математизация человеческого знания?
Вся история развития цивилизации на Земле проникнута идеями числа и измерения. За несколько тысячелетий существования и совершенствования математикой выработан особый язык абстракций, который позволяет привести к единому виду описание самых разнообразных по своей природе объектов и процессов. Любая наука получает ранг точной только тогда, когда она в достаточной мере использует эту систему универсальных методов анализа, вырабатывая хорошо развитую систему строгих понятий, позволяющих делать широкие теоретические обобщения и предсказания. Математическое моделирование является одним из важнейших этапов венчающим переход науки в разряд точных.
Возникает вопрос, зачем нужны модели? Сформировать интуитивное представление о понятии модель помогут простые примеры: прежде, чем воздвигнуть зданиеневиданного типа, архитектор сооружает это здание из кубиков на столе, чтобы увидеть, как оно будет выглядеть.Перед тем как запустить в производство новый самолет, его помещают в аэродинамическую трубу и с помощью соответствующих датчиков определяют величины напряжений, возникающих в различных местах конструкций и т.д.
После всего сказанного становится понятным такое определение.
Модель — это такой материальный или мысленно представляемый объект, который в процессе изучения замещает объект — оригинал, сохраняя некоторые важные для данного исследования типичные его черты.
Человек применяет модели,при изучении сложных процессов, явлений, конструировании новых сооружений и т.п.,с незапамятных времен. Хорошо построенная модель, как правило, доступнее для исследования, нежели реальный объект. Более того, некоторые объекты вообще не могут быть изучены непосредственным образом: недопустимы, например, эксперименты с экономикой страны в познавательных целях; принципиально неосуществимы эксперименты с прошлым или, скажем, с планетами Солнечной системы и т.д.
Хорошая модель, как правило, обладает удивительным свойством: ее изучение дает некоторые новые знания об объекте — оригинале. Это, безусловно, очень важное свойство, играющее притягательную роль для лиц, занимающихся построением и изучением моделей
Моделирование — процесс построения модели. Существует несколько приемов моделирования, которые можно условно объединить в две большие группы: материальное (предметное) и идеальное моделирование.
К материальным относятся такие способы моделирования, при которых исследование ведется на основе модели, воспроизводящей основные геометрические, физические, динамические и функциональные характеристики изучаемого объекта. Основными разновидностями материального моделирования являются физические и аналоговое моделирование.
Физическим называют моделирование, при котором реальному объекту сопоставляется его увеличенная или уменьшенная копия, допускающая исследование в лабораторных условиях с помощью последующего перенесения свойств изучаемых процессов и явления с модели на объект на основе теории подобия. Аналоговое моделирование основано на аналогии процессов и явлений, имеющих различную физическую природу, но одинаково описываемых одними и теми же математическими уравнениями, логическими схемами, т.п.. Наиболее простой пример — изучение механических колебаний с помощью электрической схемы, описываемой теми же дифференциальными уравнениями.
Идеальное моделирование носит теоретический характер. Различают два типа идеального моделирования: интуитивное и знаковое. Под интуитивным понимаем моделирование, основанное на интуитивном представлении об объекте исследования, не поддающемся формализации либо не нуждающемся в ней. В этом смысле, например, жизненный опыт каждого человека может считаться его интуитивной моделью окружающего мира.
Знаковым называется моделирование, использующее в качестве моделей знаковые преобразования какого-либо вида: схемы, графики, чертежи, формулы, наборы символов и т.д., а также включающее совокупность законов по которым можно оперировать с выбранными знаковыми образованиями и их элементами.
Важнейшим видом знакового моделирования является математическое моделирование, при котором исследование объекта осуществляется посредством модели, сформулированной на языке математики, с использованием тех или иных математических методов.
Классическим примером математического моделирования является описание и исследование И. Ньютоном основных законов механики средствами математики.
Библиографический список:
1.Амосов А.А., Дубинский Ю.А., Копченова Н.П. Вычислительные методы для инженеров. — М.: Мир,2008. — 575 с.
2. Бахвалов Н.С., Жидков Н.П., Кобельков Г.Г. Численные методы. 8-е изд. -М.: Лаборатория Базовых Знаний, 2010. — 624 с.
3.Косарев В.И. 12 лекций по вычислительной математике. 2-е изд. — М.: Изд-во МФТИ, 2000. — 224 с.
Источник
Математика – инструмент познания мира

Математика всегда сопровождала человека в жизни. Она помогает развитию других наук, она развивает у человека такие важные качества личности, как логическое мышление, целеустремлённость, сильную волю, устойчивое внимание, сосредоточенность, хорошую память, умение логически мыслить: сравнивать, сопоставлять, классифицировать, способность к творчеству и научной фантазии, чувство предвидения, умение прикидывать и оценивать результаты, работоспособность, чёткость и реализм в своих суждениях и выводах, находчивость и смекалку, чувство юмора.
Просмотр содержимого документа
«Математика – инструмент познания мира »
Математика – инструмент познания мира
Математика всегда сопровождала человека в жизни. Она помогает развитию других наук, она развивает у человека такие важные качества личности, как логическое мышление, целеустремлённость, сильную волю, устойчивое внимание, сосредоточенность, хорошую память, умение логически мыслить: сравнивать, сопоставлять, классифицировать, способность к творчеству и научной фантазии, чувство предвидения, умение прикидывать и оценивать результаты, работоспособность, чёткость и реализм в своих суждениях и выводах, находчивость и смекалку, чувство юмора.
А такие качества, как интуиция, вдохновение, озарение, ведут к великим открытиям в науке. «В любом открытии есть 99% труда и потения и только 1% таланта и способностей»,- говорил Л.Магницкий. «Вдохновение – это такая гостья, которая не любит посещать ленивых», — заметил он.
Она представляет из себя науку точную, не терпящую произвола в толковании и различных спекуляций. Это воплощение порядка и жесткой логики. Она помогает понять мир вокруг нас, узнать больше о его законах, так как эти законы подчинены тому же самому порядку, что царит в математике!
Язык, на котором говорит природа, мы успешно можем перевести на язык математики и осознать структуру взаимосвязей какого-либо явления. И, после того, как мы эти связи формализуем, мы можем строить модели, предсказывать будущие состояния явлений, которые этими моделями описываются, только лишь на бумаге или внутри памяти вычислительных машин!
Эйнштейн, в ответ на вопрос, где находится его лаборатория, улыбнулся и указал на карандаш и бумажный лист.
Его формулы теории относительности стали важным этапом на пути познания вселенной в которой мы живем. И это произошло до того, как человек начал осваивать космос и только тогда экспериментально подтвердил правильность уравнений великого ученого!
Благодаря применению математики нам не нужно проводить дорогостоящие и опасные для жизни эксперименты, прежде чем реализовать какой-нибудь сложный проект, например, в освоении космоса. Мы можем заранее рассчитать параметры орбиты космического аппарата, запускаемого с земли для доставки космонавтов на орбитальную станцию. Математические расчеты позволят не рисковать жизнью людей, а прикинуть заранее все необходимые для запуска ракеты параметры, обеспечив безопасный полет.
Конечно модель она на то и модель, что не может учесть все возможные переменные, поэтому и случаются катастрофы, но все равно она обеспечивает довольно надежные прогнозы.
Медицина и здравоохранение — тоже существует благодаря математике, которая используется, во-первых при проектировании медицинских приборов, а во-вторых, при анализе данных об эффективности того или иного лечения.
Зачем нужна математика человеку? Какие способности она развивает?
Итак, мы выяснили, что математика является одним из самых важных достижений культуры и цивилизации. Без нее развитие технологий и познание природы были бы немыслимыми вещами!
Математика развивает умственные способности
Математика позволяет развить некоторые важные умственные качества. Это аналитические, дедуктивные (способность к обобщению), критические, прогностические (умение прогнозировать, мыслить на несколько шагов вперед) способности.
Также эта дисциплина улучшает возможности абстрактного мышления (ведь это абстрактная наука), способность концентрироваться, тренирует память и усиливает быстроту мышления. Если говорить более подробно и оперировать конкретными навыками, то математика поможет человеку развить следующие интеллектуальные способности
Умение обобщать. Рассматривать частное событие в качестве проявления общего порядка. Умение находить роль частного в общем.
Способность к анализу сложных жизненных ситуаций, возможность принимать правильное решение проблем и определяться в условиях трудного выбора.
Умение находить закономерности.
Умение логически мыслить и рассуждать, грамотно и четко формулировать мысли, делать верные логические выводы.
Способность быстро соображать и принимать решения.
Навык планирования наперед, способность удерживать в голове несколько последовательных шагов.
Навыки концептуального и абстрактного мышления: умение последовательно и логично выстраивать сложные концепции или операции и удерживать их в уме.
Математика необходима для развития ребенка!
Особенно математика важна для развития ребенка! Она задает стандарты правильного, рационального мышления на всю жизнь вперед! Дает огромный толчок для умственного развития.
Я даже не знаю, какой другой школьный предмет способен настолько поднять умственный уровень подрастающего индивида и послужить таким хороши подспорьем для интеллектуального развития в последствии, уже в зрелом возрасте. Я не имею ввиду математику только как предмет, алгебру или арифметику, я говорю о применении математических методов вообще, в том числе в физике, в геометрии, в информатике и т. д.
Математика организует, упорядочивает и оптимизирует ваше мышление —
Можно сказать словами известного изречения Ломоносова, великого ученого, который достиг успеха как на почве естественных наук так и в области гуманитарных дисциплин — редчайший случай универсального ума. Он говорил: «Математику только зачем учить надо, что она ум в порядок приводит.»
Математика тренирует, такие умственные качества, которые формируют каркас и скелет всего вашего мышления! Это, в первую очередь, логические способности. Это все то, что организует все ваши мысли в связанную систему понятий и представлений и связей между ними.
Математика сама является воплощением природного порядка и нет ничего удивительного в том, что она упорядочивает ваш ум. А без этой пресловутой логики в голове человек не способен делать верные логические выводы, сопоставлять понятия разного рода, он теряет способность к здравому анализу и рассуждению. Что может повлечь явление «каши в голове», путаницы в мыслях и рассуждениях, невнятность аргументации.
Такого человека легко вводить в заблуждение, что собственно обычно и происходит, так как он не способен выявить явное нарушение логики в утверждениях всяких махинаторов и шарлатанов (Уже второй плаченый опыт с финансовыми пирамидами в нашей стране говорит о том, что огромная часть людей считает, что математика им не нужна). Знание математики не позволяет вас обмануть!
Систематические занятия математикой обогащают человека, облагораживают его. Тот, кто хоть раз испытал радостное чувство от решения трудной задачи, познал радость пусть маленького, но всё же открытия, так как каждая задача в математике – это проблема, к решению которой человечество порою шло долгие сто и тысячелетия, — тот будет стремиться познать ещё и использовать полученные знания в жизни.
Во многих современных профессиях нужны математические знания: агроному и инженеру, рабочему и доярке, космонавту и дипломату, продавцу и кассиру. Даже домохозяйке – для ведения домашнего хозяйства, для ремонта квартиры, для посещения магазина, почты, телеграфа и т. д.
Математика – это орудие, с помощью которого человек познаёт и покоряет себе окружающий мир. Чтобы сделать в математике открытие, надо любить её так, как любил её каждый из великих математиков, как любили и любят её десятки и сотни других людей. Сделайте хотя бы малую часть того, что сделал каждый из них, и мир навсегда останется благодарным вам. Полюбите математику!
Источник