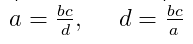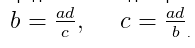Математика 6 класс пропорции способы решения задач

Задачи на пропорции

О чем эта статья:

5 класс, 7 класс, 8 класс

Понятие пропорции

Чтобы решать задачи на тему пропорции, вспомним главное определение.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин.

Главное свойство пропорции:

Произведение крайних членов равно произведению средних.

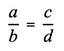
где a, b, c, d — члены пропорции, a, d — крайние члены, b, c — средние члены.

Вывод из главного свойства пропорции:

• Крайний член равен произведению средних, которые разделены на другой крайний. То есть для пропорции a/b = c/d:
  
• Средний член равен произведению крайних, которые разделены на другой средний. То есть для пропорции a/b = c/d:
  

Решить пропорцию — значит найти неизвестный член. Свойство пропорции — главный помощник в решении.

Рассмотрим легкие и сложные задачи, которые можно решить с помощью пропорции. 5, 6, 7, 8 класс — неважно, всем школьникам полезно проанализировать занимательные задачки.

Задачи на пропорции с решением и ответами

Свойства пропорции придумали не просто так! С их помощью можно найти любой из членов пропорции, если он неизвестен. Решим 10 задач на пропорцию.

Задание 1. Найти неизвестный член пропорции: x/2 = 3/1

В этом примере неизвестны крайние члены, поэтому умножим средние члены и разделим полученный результат на известный крайний член:

Задание 2. Найти неизвестный член: 1/3 = 5/y

Задача 3. Решить пропорцию: 30/x = 5/8

Задание 4. Решить: 7/5 = y/10

Задание 5. Известно, что 21x = 14y. Найти отношение x — к y

Сначала сократим обе части равенства на общий множитель 7: 21x/7 = 14y/7.

Теперь разделим обе части на 3y, чтобы в левой части убрать множитель 3, а в правой части избавиться от y: 3x/3y = 2y/3y.

После сокращения отношений получилось: x/y = 2/3.

На следующем примере мы узнаем как составить пропорцию по задаче💡

Задание 6. Из 300 подписчиков в инстаграм 108 человек — поставили лайк под постом. Какой процент всех подписчиков составляют те, кому понравился пост и они поставили лайк?

Примем всех подписчиков за 100% и запишем условие задачи кратко:

Составим пропорцию: 300/108 = 100/x.

Найдем х: (108 * 100) : 300 = 36.

Ответ: 36% всех подписчиков поставили лайк под постом.

Задание 7. Подруга Гарри Поттера при варке оборотного зелья использовала водоросли и пиявки в отношении 5 к 2. Сколько нужно водорослей, если есть только 450 грамм пиявок?

• Составим пропорцию: 5/2 = x/450.
• Найдем х: (5 * 450) : 2 = 1125.

Ответ: на 450 грамм пиявок нужно взять 1125 гр водорослей.

Задание 8. Известно, что арбуз состоит на 98% из воды. Сколько воды в 5 кг арбуза?

Вес арбуза (5 кг) составляет 100%. Вода — 98% или х кг.

Ответ: в 5 кг арбуза содержится 4,9 кг воды.

Перейдем к примерам посложнее. Рассмотрим задачу на пропорции из учебника по алгебре за 8 класс.

Задание 9. Папин автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Составим пропорцию: v1/v2 = t2/t1.

Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

t2 = (75 * 13)/52 = 75/4 = 18 3/4 = 18 ч 45 мин

Ответ: 18 часов 45 минут.

Задание 10. 24 человека за 5 дней раскрутили канал в телеграм. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.

3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию:

Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член:

Значит, 30 человек раскрутят канал за 4 дня.

Источник

Что такое пропорция

О чем эта статья:

Что такое пропорция

Пропорция — это равенство двух отношения.

Пропорциональный — это такой, который находится в определенном отношении к какой-либо величине.

Пропорция всегда содержит равные коэффициенты.

Если выразить определение формулой, то выглядеть оно будет так:

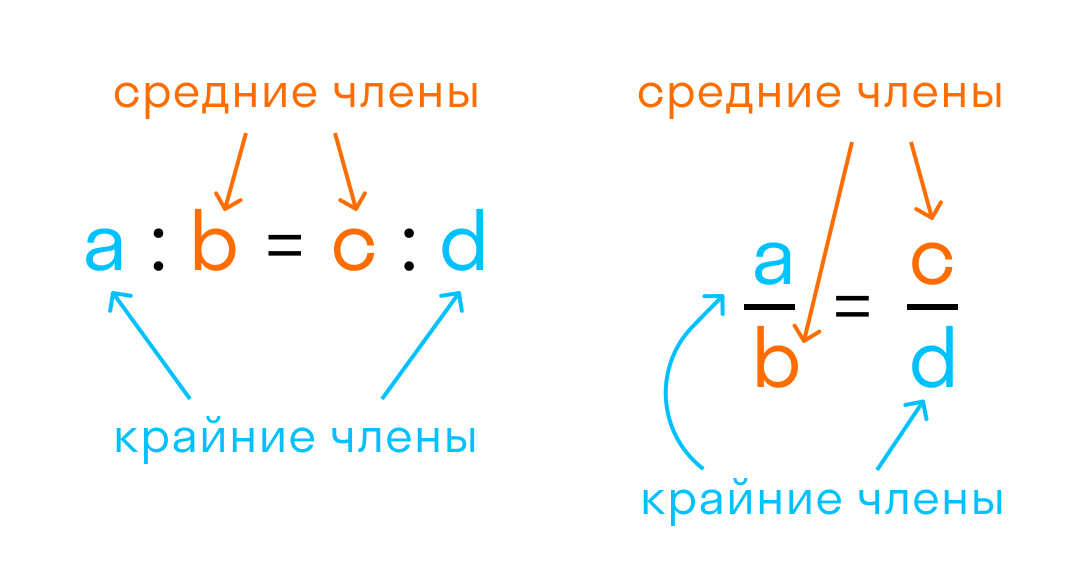
• a : b = c : d

• 

a и d — крайние члены пропорции

Читается это выражение так: a так относится к b, как c относится к d

Например:

Это равенство двух отношений: 15 так относится к 5, как 9 относится к 3.

15 и 3 — крайние члены пропорции.

5 и 9 — средние члены пропорции.

Наглядный пример для понимания:

У нас есть восемь кусочков аппетитной пиццы и, предположим, четыре голодных друга.

• Запишем эту непростую ситуацию в виде отношения 8 кусочков к 4 голодным друзьям: 8 : 4
• Далее преобразовываем это отношение в дробь: 8/4
• Выполняем деление: 8/4 = 2

Это значит, что 8 аппетитных кусочков пиццы будут так относиться к 4 голодным друзьям, что каждому голодающему достанется по 2 кусочка. Прекрасно!

А теперь представим, ситуацию, в которой есть только половина аппетитной пиццы, но при этом и голодных друга — всего два.

Что мы имеем: 4 кусочка и 2 друга, претендующих на них.

• Запишем в виде отношения: 4 : 2
• Преобразовываем получившееся отношение в дробь: 4/2
• Выполняем деление: 4/2 = 2

Это значит, что 4 аппетитных кусочка будут так относиться к 2 голодным друзьям, что каждому из них достанется по 2 кусочка.

Оценив обе ситуации, делаем вывод, что отношение 8/4 пропорционально отношению 4/2. Отношения в пропорции — равные.

Вывод: знание математических пропорций пригодится при заказе пиццы. Быстренько прикидываем отношение количества человек, претендующих на пиццу, и число кусочков — и сразу заказываем побольше пиццы, чтобы никто не остался голодным😉

Основное свойство пропорции

Запомните основное свойство пропорции:

Произведение крайних членов пропорции равно произведению средних членов этой пропорции.

В виде формулы свойство выглядит так:

a : b = c : d = a * d = b * c

Мы знаем, что a и d — крайние члены пропорции, b и c — средние.

Это свойство следует применять, чтобы проверить пропорцию. Если все сходится согласно формулировке — пропорция составлена верно, и отношения в пропорции являются равными друг другу.

Давайте проверим несколько пропорций.

Пример 1. Дана пропорция:6/2 = 12/4

• Чтобы проверить, верно ли составлена пропорция, перемножаем ее крайние члены: 6 * 4 = 24.
• Далее перемножаем средние члены пропорции: 2 * 12 = 24
• Произведение крайних членов пропорции равно 24, произведение средних членов пропорции также равно 24.
• 6 * 4 = 2 * 12
  24 = 24

Делаем вывод, что пропорция 6/2 = 12/4 составлена верно.

Пример 2. Дана пропорция: 10/2 = 16/4

• Перемножаем крайние члены пропорции: 10 * 4 = 40.
• Перемножаем средние члены: 16 * 2 = 32.
• Произведение крайних членов пропорции равно 40. Произведение средних членов пропорции равно 32.
• 10 * 4 ≠ 16 * 2
  40 ≠ 32

Отсюда делаем вывод, что отношения в пропорции 10/2 ≠ 16/4 не являются равными.

Примеры решения задач с пропорцией

Чтобы потренироваться в составлении пропорций, решим вместе несколько задачек.

Задачка 1. Дана математическая пропорция: 15/3 = x/4

1. По основному свойству пропорции перемножаем множители:
   15 * 4 = 3x
2. Получаем уравнение: 60 = 3x
3. 60/3 = x
   x = 20.

Ответ: в пропорции 15/3 = x/4, x = 20

Задачка 2. Найдите четвертый член пропорции: 18, 9 и 24.

1. Записываем чиcла в виде дробей: 18/9 = 24/x
   Где x — четвертый член пропорции.
2. По основному свойству пропорции, перемножаем средние члены: 9 * 24 = 216
3. Выводим уравнение 18x = 216
4. Находим x:
   x = 216 : 18
   x = 12
5. Проверяем: 9 * 24 = 216, 18 * 12 = 216.
   Пропорция составлена верно.

Ответ: четвертый член пропорции — 12.

Задачка 3. 18 человек могут съесть пять килограммов суши за 8 часов, сколько часов понадобится 9 людям?

1. Записываем числа в виде дроби: 18/9 = x/8
2. Перемножаем множители по основному свойству пропорции: 18 * 8 = 9x
3. Находим х:
   144 = 9x
   144 : 9 = 16

Ответ: 16 часов понадобится 9 людям, чтобы съесть все суши.

Задачка 4. Дана пропорция: 20/2 = y/4

1. По основному свойству пропорции перемножаем множители:
   20 * 4 = 2y
2. Получаем уравнение: 80 = 2y
3. Находим у:
   80/2 = y
   x = 40.
4. Проверяем пропорцию: 20 * 4 = 80, 40 * 2 = 80.

Источник

Математика. 6 класс

Конспект урока

Перечень рассматриваемых вопросов:

• Понятие пропорции.
• Основное свойство пропорции.
• Как правильно составить пропорцию.
• Как найти неизвестный член пропорции.

Равенство двух отношений называют пропорцией.

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

1. Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.

1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.

Теоретический материал для самостоятельного изучения

Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.

Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.

Рассмотрим 3 способа нахождения неизвестного члена пропорции.

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

№2. Тип задания: Подстановка элементов в пропуски в тексте.

Найдите неизвестный член пропорции.

Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.

Источник