Математический способ обработки результатов

Методы математической обработки

Кметодам обработки количественных данных от­носятся статистические приемы подведения итогов исследования, выявления определенных связей меж­ду ними, проверки достоверности выдвинутой гипотезы. Математическая обработка результатов обеспечивает доказательность (репрезентативность) иссле­дований. В сочетании с качественными показателя­ми количественная обработка значительно повышает объективность психологического исследования.

Достоверность выводов исследования не только определяется совершенством примененного математического аппарата, но также зависит от того, на­сколько адекватно величины, которыми мы опериру­ем, отражают реальные количественные характери­стики изученных явлений иобъектов. Несоблюдениеэтого требования превращает математическую обра­ботку в пустое манипулирование формулами.

Нахождение решающих количественных критериев для оценки тех или иных факторов и сторон обучения или воспитания не является математической проблемой. Это задача, которая решается психологическими исследованиями. Однако, чтобы ее решать, надо правильно измерять психологические явления, учитывая условия и границы применимости спосо­бов измерения.

Измерение — это приписывание чисел объектам и событиям в соответствии с определенными правила­ми. Простейший способ приписывания числовых характеристик предметам и явлениям – их регистрация. Она заключается в том, что выделяют какой-нибудь признак и отмечают каждый случай, когда в наблюде­нии или эксперименте появляется предмет или явле­ние с этим признаком. Так, например, при изучении мотивов учения на основе анкетного опроса определя­ют число студентов, выбравших тот или иной вариант ответа. Статистическая обработка результатов регист­рирующего изучения позволяет сделать некоторые важные обобщения и выводы относительно всей сово­купности изучаемых явлений в целом.

Важная особенность регистрации состоит в том, что она позволяет применять количественное изуче­ние даже там, где невозможно определить сами свой­ства изучаемых явлений, что очень часто встречается в психолого-педагогических исследованиях.

Так, например, невозможно прямо измерить уро­вень знаний и умений студентов, развития тех или иных нравственных качеств, степень эффективности данного метода обучения и т. д. Но, регистрируя со­ответствующие события[21]: ошибки, поступки, прояв­ления и т. д., — можно получать определенные коли­чественные характеристики всех этих признаков, устанавливать их частотность, а значит, определять возможные закономерности их проявления.

Для определения границы применимости регист­рации нужно как можно точнее сформировать крите­рий, позволяющий однозначно отличить объект с ре­гистрируемым признаком от объекта без него. Так, на­пример, прежде чем количественно определить про­фессиональную направленность студентов, нужно дать ее четкую формулировку и определить критерии, которые должны быть научно обоснованы. Иначе трудно будет судить о репрезентативности выводов.

Следующий способ количественной характери­стики данных — операция упорядочения. Сущность ее заключается в том, что изучаемые явления распре­деляются в порядке возрастания или убывания вели­чины определенного признака. Затем каждой группе объектов присваивается число, соответствующее месту этой группы в нарастающем или убывающем ряду. Это число, показывающее порядок изучаемого признака у данных объектов, называется их рангом.

После упорядочения данных часто осуществляют их группировку. Для этого определенный интервал значений изучаемого признака принимается за еди­ницу меры. Значение признака в исследуемых явле­ниях будет определяться числом, показывающим, сколько раз данная единица меры укладывается в на­блюдаемой величине. Условия, налагаемые на «ин­тервальное» измерение, значительно строже, чем при регистрации или упорядочении:

• наличие объективного эталона величины при­знака, принятого за единицу меры;

• возможность прямо или косвенно сопоставлять любое измеряемое явление с этим эталоном;

• неизменность измеряемых признаков в течение нужного периода времени.

Выполнение этих трех условий не всегда удается в психологических исследованиях, отсюда трудности измерений и сложности применения аппарата мате­матики.

Полученные в результате измерения количествен­ные характеристики обрабатываются методами мате­матической статистики, позволяющими обобщить эмпирические результаты, объяснить причины «слу­чайного» результата, дать ему определенное вероят­ностное толкование.

Наиболее распространенными методами обра­ботки количественных данных в прикладной психологии являются дисперсионный, корреляционный и факторный анализ.

Дисперсионный анализ (от лат. dispersio — рассеива­ние) — статистический метод, позволяющий анали­зировать влияние различных факторов на исследуе­мую переменную. Суть дисперсионного анализа за­ключается в разложении (дисперсии) измеряемого признака на независимые слагаемые, каждое из кото­рых характеризует влияние того или иного фактора или их взаимодействия. Последующее сравнение та­ких слагаемых позволяет оценить значимость каждо­го изучаемого фактора, а также их комбинации. При этом особую роль играет анализ средних значений (отклонение от которых и называют дисперсией).

При осуществлении дисперсионного анализа ре­зультаты наблюдений группируются с учетом града­ций каждого учитываемого фактора (возраста, уров­ня образования, отдельных психологических особен­ностей и т. д.). Если учитываемый фактор оказывает влияние на признак, средние результирующего при­знака изменяются в соответствии с градациями фактора. Внутри каждой такой группы обнаруживается своя дисперсия, связанная с действиями других факторов.

Дисперсионный анализ допускает статистическое исследование признаков, выраженных не только в абсолютных количественных единицах, но и в отно­сительных или условных баллах и индексах.

Корреляционный анализ (от лат. correlatio — соотно­шение) — статистический метод оценки формы, зна­ка и тесноты связи исследуемых признаков или фак­торов. При определении формы связи рассматрива­ется ее линейность или нелинейность (т. е. как в сред­нем изменяется в зависимости от изменения х, а х — от у).

Одним из основных принципов определения ко­личественных критериев корреляционной связи — коэффициентов корреляции — является сравнение величин отклонений от среднего значения по каждой группе в сопряженных парах сравниваемых рядов пе­ременных.

С целью достижения независимости меры корре­ляционной связи от числа сравниваемых пар и вели­чин стандартных отклонений в двух группах произве­дение отклонений делится на число сравниваемых пар и стандартные отклонения в сопоставимых ря­дах. Такая мера носит название коэффициента кор­реляции — произведения моментов Пирсона.

Коэффициент корреляции — математический по­казатель силы связи между двумя сопоставляемыми статистическими признаками. Величина коэффици­ента колеблется в пределах от —1 до +1. Смысл край­них значений коэффициента состоит в следующем:

• коэффициент равен +1, значит, связь между признаками однозначна по типу прямо пропорцио­нальной зависимости;

• коэффициент корреляции равен —1, следова­тельно, связь также является функциональной, но по типу обратной пропорциональности;

• нулевая величина коэффициента свидетельст­вует об отсутствии связи между признаками.

Статистическую значимость коэффициента кор­реляции определяют по таблицам.

Факторный анализ (от лат. factor — действующий, производящий и греч. analysis — разложение, расчле­нение) — метод многомерной математической статистики, применяемый при исследовании статистиче­ски связанных признаков с целью выявления опреде­ленного числа скрытых от непосредственного наблюдения факторов.

С помощью факторного анализа не просто уста­навливается связь изменения одной переменной с изменением другой переменной, а определяется мера этой связи и обнаруживаются основные факторы, лежащие в основе указанных изменений. Факторный анализ особенно продуктивен на начальных этапах научных исследований, когда необходимо выделить какие-либо предварительные закономерности в исследуемой области. Поэтому факторный анализ представляет собой не только метод статистической обработки исходных данных для их обобщения, но и широкий научный метод подтверждения гипотез относительно природы процессов, присущих самому измеряемому свойству.

Одной из наглядных моделей факторного анализа может служить схема, приведенная на рис. 1. Области признаков (психологических особенностей, свойств, способностей и т. д.), измеряемых тестами А, В, С, представлены в виде прямоугольников. В зоне 1 на­ходятся общие признаки для тестов А и В, в зоне 2 для тестов В и С, а в зоне 3 — признаки, влияющие на успешность выполнения тестов Л и С. В зоне 4 при­сутствуют признаки, объединенные общим для сово­купности трех тестов фактором. Относительная пло­щадь зон иллюстрирует факторный вес — меру выра­жения выявленной латентной переменной (призна­ка) в результатах того или иного теста, т.е. представленность в результатах теста данных выделенного универсального фактора Х_АБС.

Рис. 1. Модель факторного анализа

Исходной информацией для проведения фактор­ного анализа является корреляционная матрица, или матрица интеркорреляций показателей тестов. Выде­ленные путем анализа интеркорреляций или других характеристик связи обобщенные факторы первого

порядка могут быть представлены в виде новой мат­рицы, отражающей корреляции между факторами. Нa основе таких матриц могут определяться факторы более высокого порядка.

В настоящее время методы факторного анализа составляют сложную специальную область матема­тической статистики. В психологической диагности­ке факторный анализ широко используется как для решения исследовательских задач, так и при конст­руировании психодиагностических методик[22].

Существуют и другие методы математической об­работки данных исследований. Мы рассмотрели наи­более распространенные. Практика исследований показывает, что математическая обработка является эффективным средством описания и установления многих важных психологических характеристик, их связей, отношений, закономерностей.

В заключение обзора методов исследования следует подчеркнуть, что нельзя ни противопоставлять одни методы другим, ни абсолютизировать возмож­ности некоторых. Выбор того или иного метода определяется предметом и задачами исследования. В любом психологическом исследовании применяется и комплекс методов, взаимно дополняющих друг друга и позволяющих получить достоверные выводы.

Методы исследования, используемые в психологии профессионального образования, имеют общепсихологическое происхождение и вместе с тем обладают своей спецификой. Близость психологии профессионального образования к психологии развития, психологии труда, возрастной и педагогической психологии обусловливает заимствование уже сложившихся методов.

[1] См.: Новиков А. М. Профессиональное образование России. — М. 1997. —С. 41.

[2] См.: Шадриков В.Д. Деятельность и способности. – М., 1994.

[3] См.: Платонов К.К. Система психологии и теория отражения. – М. 1982. – С.277 – 298.

[5] См.: Ганзен В.А. Системные описания в психологии. – Л., 1984

[6] Панельное исследование предполагает неоднократное изучение одного и того же социального объекта с определенными временными интервалами при неизменной программе исследования.

[7] См.: Ананьев Б.Г. О проблемах современного человекознания. – М., 1977. – С. 295-298.

[8] См.: Введение в психологию / Под ред. А.В. Пестровского. – М., 1993.

[9] См.: Годвруа Ж. Что такое психология: В 2 т.- М., 1992. – Т.1.

[10] См.: Benesch A. Atlas zur Psychologie. – Munchen, 1992. – Bd 1.

[11] Демоскопия – опрос мнений определенной рапрезентативной социальной группы населения.

[12] Коакцион – опрос мнений на основе принятия другой социальной роли.

[13] См.: Орлов А.Б. Основные исследовательские методы возрастной и педагогической психологии // Вопр. Психологии. – 1981. — №1.

[14] См.: Anvtndungsbezogene Arbeits -, Betriebs – und Organisationspsychologie. – Gottingen, 1994.

[15] См.: Анастази А. Психологическое тестирование: В 2 кн.: Пер. с англ. – М., 1982. – Кн. 2. – С.94-97.

[16] См.: Словарь-справочник по психологической диагностике / Сост. Л.Ф. Бурлачук, С.М. Морозов. – Киев, 1989. – С. 93.

[17] См.: Психологические проблемы неуспеваемости школьников / Под ред. Н.А. Менчинской. – М., 1991.

[18] См.: Калмыкова З.И Психологические принципы развивающего обучения. – М., 1979.

[19] См.: Проблемы методологии педагогики и методики исследования / Под ред. М. А. Данилова, Н. И. Болдырева. – М., 1971. – С. – 231.

[20] Давыдов В. В. О двух основных этапах развития детской и педагогической психологии // Психология воспитания и обучения. – М., 1978. – Вып. 5. – С. 4-5.

[21] Событие – одно из вероятных явлений.

[22] См.: Бурлачук Л.Ф. Словарь-справочник по психодиагностике / Л.Ф. Бурлачук, С.М. Морозов. – СПб., 1999. – С. 361 – 362.

Источник

Математические методы исследования в обработке эмпирических данных научного труда

Эмпирическое исследование основывается на данных, полученных опытно-логическим путем. Зачастую оно сводится к изучению актуальных научных трудов, которые фактически выступают в качестве «инструкции» по проведению практического раздела. Аналитический раздел эмпирического научного проекта основывается на материалах, полученных в ходе эксперимента, наблюдения или иного способа сбора информации. Обработка полученных данных происходит с помощью математических методов, которые позволяют конкретизировать проблему и привести исследователя к более точному результату.

Эмпирическое исследование основывается на данных, полученных опытно-логическим путем. Зачастую оно сводится к изучению актуальных научных трудов, которые фактически выступают в качестве «инструкции» по проведению практического раздела. Аналитический раздел эмпирического научного проекта основывается на материалах, полученных в ходе эксперимента, наблюдения или иного способа сбора информации. Обработка полученных данных происходит с помощью математических методов, которые позволяют конкретизировать проблему и привести исследователя к более точному результату.

Основные задачи математической обработки эмпирических данных научной работы

Применение математических приемов в ходе обработки и анализа эмпирических данных позволяет исследователю решить следующие задачи:

— оценить достоверность выдвинутой гипотезы и выявить отличия от себе подобных;

— провести корреляционный анализ, который помогает установить зависимость гипотезы от конкретных критериев, условий и пр.;

— факторный анализ: помогает определить структуру объекта исследования, а также оценить степень влияния конкретного элемента, звена или переменной на результативный показатель;

— провести анализ изменчивости признаков, то есть уточнить, как себя поведет объект исследования при изменении определенных условий, параметров. Чаще всего такой ход используется в психологии.

Этапы математической обработки данных эмпирического исследования

Итак, все необходимые для анализа сведения уже на руках у исследователя. Чтобы доказать выдвинутую гипотезу не всегда достаточно провести сравнительный анализ суждений с уже доказанными теориями, порой требуется предъявить неопровержимые доказательства. Как же их получить? Ответ прост. Если логика автора может завести его в дебри или быть ошибочной, то цифры никогда не врут. Одним из эффективнейших способов обработки данных является использование математических методов. Он применим фактически к любым научным трудам и типам данных, в том числе эмпирическим.

Ключевыми элементами математического анализа эмпирических данных научной работы являются: признак, показатель, переменная и параметр. Все эти 4 категории характеризуют конкретное значение, числовую единицу (величину) того, что было выявлено у объекта исследования.

Пять этапов

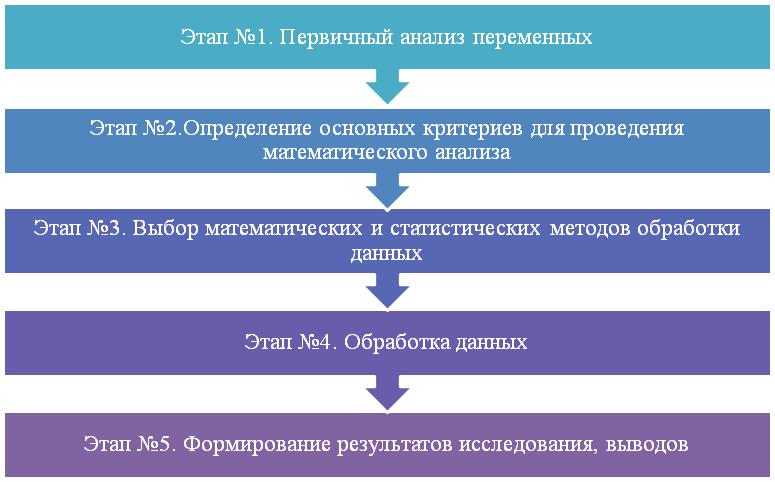
Математическая обработка эмпирических данных проходит ряд этапов:

Нужна помощь преподавателя?

Мы всегда рады Вам помочь!

Этап №1. Первичный анализ переменных.

Здесь исследователю необходимо отсортировать все собранные материалы, определить признаки и критерии, по которым будет разбита информация, и оформить ее в виде таблиц, графиков, диаграмм и пр.

Важно тщательно проверять все занесенные в таблицу или чертежи данные, обеспечить максимальную точность всех действий, чтобы прийти к достоверному результату, исключить ошибки и погрешности.

Этап №2. Определение основных критериев для проведения математического анализа.

На этом этапе важно правильно определить искомый фактор, а также от чего он зависит, то есть обозначить ключевой показатель и переменные. Затем следует разработать математическую модель. Обычно анализ начинается с анализа первичных статистик. В этих целях можно использовать следующие действия: среднее арифметическое, квадратное уравнение, дисперсия, разброс, медиана и пр.

Здесь важно определить, как все полученные данные будут фиксироваться и использоваться в дальнейшем. Во время анализа важно учитывать действующие ограничения (нормативы) в отношении каждого показателя, переменной.

Если для проведения исследования и анализа недостаточно данных или они не соответствуют выбранным критериям, то придется изменить метод исследования или же пересмотреть критерии.

Этап №3. Выбор математических и статистических методов обработки данных.

После того, как все сведения были упорядочены и приведены в пригодный для расчетов и иных операций вид, необходимо определить наиболее оптимальный способ их анализа посредством использования приемов математики и статистики. Данный подход позволит сделать выводы автора более аргументированными, обоснованными и точными.

Этап №4. Обработка данных.

На этом этапе автор может анализировать и сопоставлять полученные в ходе математической обработки данные вручную или с помощью специальной вычислительной техники. Сейчас таким помощником является компьютер и соответствующие программные обеспечения. Использование этих технических средств ускоряет процесс обработки данных, но для этого требуются определенные знания и навыки.

Этап №5. Формирование результатов исследования, выводов.

На основе проведенной математической обработки эмпирических данных, автору необходимо сделать определенные умозаключения. Важно расшифровать, какой параметр и что означает, какие результаты были получены и о чем они свидетельствуют. Такой подход позволит конкретизировать результат научной работы, сделать ее более аргументированной.

Трудности с учебой?

Помощь в написании студенческих и
аспирантских работ!

Источник