Некоторые математические проблемы информационной безопасности
Наряду с политическими, социально-экономическими, организационными, военными, правовыми, специальными и информационными проблемами, решение которых предусматривается на государственном, федеральном уровне, в информационной сфере существуют проблемы математического характера, о которых в работе и пойдет речь. В работе приводятся и конкретизируются некоторые важные понятия и основные положения информационной безопасности и защиты информации. Основными нормативными документами в этой сфере являются Конституция РФ — основной закон, ФЗ О безопасности, Военная доктрина и Доктрина информационной безопасности, а также руководящие документы Федеральной службы по техническому и экспортному контролю (РД ФСТЭК)
Информационная безопасность государства — состояние защищенности его национальных интересов в информационной сфере. Информационная сфера — совокупность информационной инфрастрктуктуры страны, информации, субъектов, осуществляющих сбор, формирование, распространение и использование информации, а также системы регулирования возникающих при этом общественных отношений. Информационная сфера — системообразующий фактор жизни общества, часть социальной деятельности общества.
Целью написания работы являетя стремление автора заострить внимание читателей на первоочередных математических задачах в области информационной безопасности и защиты информации, без решения которых прогресса в ближайшие годы (возможно десятилетия) ожидать не приходится.
Описание ситуации информационного взаимодействия (воздействия)
Рассматривается группа абонентов-пользователей Г =
Таким образом, достоверность, целостность, конфиденциальность, доступность должны быть обеспечены каждой паре общающихся пользователей в любой сети связи. Выполнение названных требований в сетях обеспечивается разными средствами, программно-аппаратными комплексами, реализующими достаточно сложные алгоритмы, программы, разработанные в рамках теорий электросвязи, кодирования и криптологии.
В предлагаемой работе рассматриваются основные понятия и положения криптологии, представляющей тесно взаимодействующие криптографию и криптографический анализ с примыкающей к ним стеганологией: образуемой стеганографией и стеганографическим анализом. Задачами информационного обмена, в частности, криптографии и теории кодирования являются задачи обеспечения конфиденциальности, установления подлинности абонентов и проверка целостности сообщений, обеспечение доступности субъектов к объектам и ресурсам, которая достигается распределением и разграничением доступов. Первая задача (конфеденциальность) решается применением криптографической системы (КГС), шифрованием сообщений, вторая – использованием электронной цифровой подписи (ЭЦП) и третья задача – установлением совпадения дайджестов, передаваемого и сформированного получателем. Задача обеспечения целостности решается методами теории кодов, кодированием/декодированием сообщений кодами исправляющими ошибки, корректирующими кодами. О доступности уже сказано ранее.
Общая схема реализации сеанса связи между парой абонентов (точка-точка) представлена на рисунке 1.
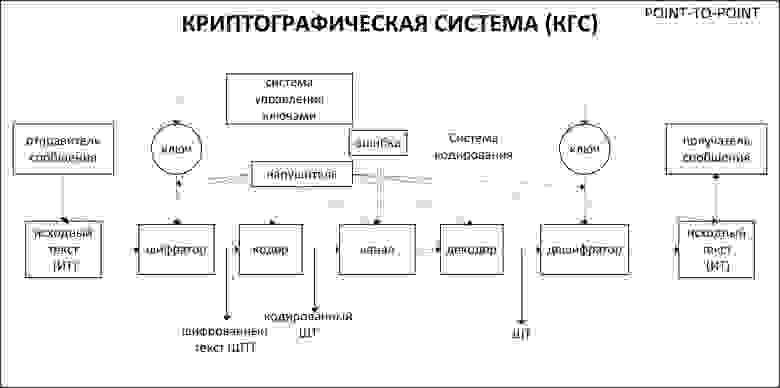
Рисунок 1 — Схема реализации сеанса связи абонентов с использованием одноключевой симметричной КГС, системы управления ключами и системы кодирования
Технология защищенного информационного обмена сообщениями
Технология информационного обмена включает субъекты, объекты, ресурсы и процессы. Субъектами являются получатель и отправитель сообщения, ресурсы (финансовые, сетевые, вычислительные, временные), объекты: источник сообщения, формирующий послание, само сообщение, ключи, вырабатываемые ключевой системой, шифрующее/дешифрующее, кодирующее/декодирующее устройство, дисплей или принтер, — то есть устройство для отображения сообщения в форму доступную для восприятия всеми субъектами получателями и отправителями.
Последовательность обработки сообщения должна быть такой как представлено на рис.1. Это связано с тем, что при наличии/отсутствии искажений шифрсообщения его дешифрование в первой ситуации с ошибками невозможно. Поэтому на стороне получателя сообщения необходимо предварительно устанавливать наличие ошибок в сообщении и внести исправления, если ошибки есть. Только после устранения ошибок возможно успешное дешифрование сообщения. Параллельно с обработкой сообщения обрабатывается цифровая подпись и выполняется ее проверка.
Одноключевая криптографическая система. Обязательными, необходимыми атрибутами сеанса связи являются идентификатор пользователя, пароль доступа и, что самое важное – ключ шифрования. В классической традиционной криптографической системе (КГС) отправитель и получатель оба используют один и тот же ключ для шифрования и дешифрования. По этой причине такие системы шифрования называют одноключевыми (симметричными). Понятно, что обе стороны должны располагать ключом до сеанса связи, т.е. ключ необходимо выработать, распределить (какую пару ключей кому) и распространить (доставить) абонентам. Это задача управления ключами. Для ее успешного решения требуется защищенный (выделенный) канал распространения ключей. Часто ключ доставлялся специальным дипкурьером. Имя одного из них Теодор Нетте широко известно и вошло в литературу и в историю.
Двухключевая криптографическая система. В 1978 году появилась публикация о новом типе КГС – двухключевой системе. Называют ее также асимметричной, системой с открытыми дверями. Отправитель и получатель сообщения используют разные ключи. По открытому ключу вычислительно очень трудно найти закрытый ключ. В этой системе каждый абонент самостоятельно формирует свою пару ключей: доступный всем отправителям открытый ключ е, которым должны пользоваться все абоненты для создания шифрсообщения, и закрытый личный ключ d получателя, который получатель хранит в тайне от всех, не разглашает его.
В таких системах отпадает необходимость в распространении ключей, что, безусловно, упрощает новую технологию защищенной связи. Но даром ничего не дается. В двухключевых системах имеются свои минусы. Шифрование в них достаточно медленный процесс. Появление подобных двухключевых систем стало возможным в связи с введением в оборот информационной безопасности нового математического объекта – односторонней функции и в множестве таких функций – функций с потайным входом (с лазейкой). Дело здесь вот в чем. Мы можем легко перемножить пару чисел р и q и получить одно число N = pq. Вычисления здесь направлены в одну сторону. Теперь допустим задано составное число N и необходимо определить его делители. Эта задача для больших чисел (10 150 -10 300 ) в настоящее время практически не решается, если нет лазейки (потайной дверцы). Такой лазейкой может быть, например, один из делителей или значение функции Эйлера от N.
В двухключевой КГС с открытым ключом получатель сообщений, который устанавливает КГС такой делитель знает, т.е. он располагает лазейкой.
Электронная цифровая подпись (ЭЦП). В цифровых подписях также используются два ключа: ключ подписи личный (не разглашаемый) и публичный (открытый) ключ проверки подписи.
Отправитель свое сообщение шифрует на открытом ключе получателя, а подписывает шифрсообщение своим закрытым ключом. Открытый ключ подписи отправителя доступен всем и получатель, используя его и проверяя цифровую подпись, убеждается, что сообщение послано и подписано этим отправителем.
Процессы в КГС. Основные процессы защищенного информационного обмена описываются в стандартах шифрования и цифровой подписи ГОСТ 28147 — 89 — для шифрования и ГОСТ 34.10 — 2012 — для ЭЦП.
При защищенном информационном обмене абонентов сообщениями реализуются следующие основные процессы. Установка КГС, выработка 4 ключей (2 для шифрования и 2 для цифровой подписи получателя), формирование сообщения, шифрование сообщения, подписание, кодирование, передача отправителем, воздействие среды и/или нарушителя, прием сообщения, декодирование, дешифрование, проверка цифровой подписи, преобразование в форму удобную для восприятия получателем. Дадим краткую характеристику процессам.
Установка КГС. Получатель А выбирает два больших простых числа рА и qА , умножает их и получает модуль шифра NА , а также вычисляет значение функции Эйлера Ф(NА ). После этого выбирает открытый ключ еА такой, что (еА , Ф(NА )) = 1, и вычисляет, используя расширенный алгоритм НОД Евклида, закрытый ключ dА , такой, что еА dА ≡1(mod Ф(NА )).
Значения (еА и NА ) и ник получателя объявляются на сетевом сервере открытыми и доступными для всех, кто будет посылать свои сообщения получателю А. Значения dА , рА , Ф(NА ), и qА сохраняются в тайне от всех. Доступ нарушителя к любой из этих величин приводит к взлому КГС.
Возможная атака на шифрсообщение. Допустим нарушителю известно Ф(NА ), и еА dА – 1 делится на Ф(NА ). Знание Ф(NА ) обеспечивает вычисление рА и qА , так как . Можно показать, что значения кратные функции Эйлера Ф(NА ) также достаточны для расчета рА и qА .
Отправитель В сформированное сообщение преобразует в числовую форму (двоичный вид) и разбивает его на блоки длины [ log2NА ] = mВi – блоки исходного текста. После этого находятся остатки mВi еА (modNА ) = уВi – блоки шифрсообщения, после чего отправляют их получателю А.
Получатель, располагая шифрованными блоками сообщения дешифрует их с использованием личного ключа, т.е. находит остатки уВi dА (modNА ) = mВi.
Математические проблемы информационной безопасности
Моделирование объектов (сетей локальных, корпоративных, глобальных, групп абонентов), процессов приема/передачи защищенных сообщений, информационного обмена и взаимодействия — обширная область со своими задачами и проблемами самого различного характера для приложений алгоритмов изучения и совершенствования информационной безопасности.
Проблемы защиты информационного обмена и информационной технологии находят свое отражение и в математических теориях, например, в теории чисел. Центральной проблемой настоящего времени является проблема разложения больших чисел на множители. В криптологии с ней связаны задачи криптографии, выбора ключевой информации, а в криптоанализе – с атаками на двухключевые КГС.
Такие атаки рассматриваются как со стороны нарушителей, так и со стороны криптоаналитиков своей стороны. Целью последних является выявление слабых мест алгоритмов и криптопротоколов. Обнаруженные уязвимости устраняются путем совершенствования продуктов, либо при невозможности их устранить переходят на новые более совершенные и современные средства.
Другой важной проблемой является получение простых чисел высокой разрядности и в массовых количествах. В компьютерных сетях и сетях связи обмен защищенными сообщениями требует от систем управления ключами массового изготовления простых чисел, которые выбираются из полного множества случайным образом. Ранее говорилось, что каждый абонент сети формирует для себя, по крайней мере, 4 ключа, которые он должен обновлять через определенные промежутки времени. Это означает, что потребность в простых числах существует постоянно, так как число пользователей пока только увеличивается. Мобильные телефоны сегодня имеет практически каждый житель развитых стран и большая часть жителей стран развивающихся. Системы сотовой связи охватывают все большие территории и остановки этого процесса в ближайшее время не предвидится.
Тесно к названной проблеме примыкает проблема установления простоты числа большой разрядности.
Проблема дискретного логарифма. Протокол Диффи – Хеллмана обеспечения ключами (DHDLP, 1976г). Абоненты А и В выбирают простое число р и простое g с порядком p -1 по модулю р, т.е. g p-1 ≡1(mod p), но g n ≠1(mod p), для любого n
n (mod p), g m (mod p) и каждый из абонентов результат своих вычислений посылает другому. Далее оба вычисляют значения, и В: k ≡ g nm ≡( g n ) m (mod p), т.е. абоненты теперь располагают одинаковыми значениями ключа, который не передавался по каналу связи через сеть и не мог быть там перехвачен. Получилась симметричная КГС.
Нарушитель может перехватить и располагать значениями g n (mod p), g m (mod p), но их использования для быстрого получения n и m или k ≡ g nm (mod p) недостаточно.
Подобная проблема дискретного логарифма сушествует и для эллиптических кривых (ЭК) над конечными полями (ЕСDLP,1985 г. Н.Коблиц, В. Миллер). На ЭК Е(Fр) появляется абелева группа, образованная точками этой кривой. Эта группа циклическая и очень большого порядка. Другими словами, при заданных двух точках ЭК Е(Fр) над полем Fp, точки Р, Q∈Е(Fр) требуется найти такое число λ (при его существовании), что Q= [λ]P.
Источник
Методы и модели защиты информации. Часть 1. Моделироваание и оценка
В книге рассмотрены вопросы моделирования и обеспечения защиты информации при наличии программно-аппаратных уязвимостей. Проведен анализ зарубежных банков данных уязвимостей
Оглавление
- Список сокращений
- Список обозначений
- Введение
- 1 Анализ классификаций и математических методов описания уязвимостей
Приведённый ознакомительный фрагмент книги Методы и модели защиты информации. Часть 1. Моделироваание и оценка предоставлен нашим книжным партнёром — компанией ЛитРес.
1 Анализ классификаций и математических методов описания уязвимостей
1.1 Постановка задачи
В области информационной безопасности под уязвимостью понимается недостаток в вычислительной системе, используя который возможно нарушить ее целостность и вызвать некорректную работу.
Попытка реализации уязвимости называется атакой.
Цель данной главы — проведение обзора способов классификаций и математических моделей систем защиты информации от утечки информации.
Для достижения поставленной цели, необходимо провести обзор:
· и анализ классификаций уязвимостей автоматизированных систем;
· базы данных уязвимостей NVD (National Vulnerability Database) и ее компонент;
· множества протоколов SCAP (Security Content Automation Protocol) как средства управления уязвимостями базы данных NVD, и языка Open Vulnerability Assessment Language как справочной реализации подмножества SCAP;
· математических моделей систем защиты информации.
1.2 Классификации уязвимостей автоматизированных систем
С целью изучения и анализа уязвимостей, а также способов их реализации в автоматизированных системах, исследователи предлагают различные виды классификации уязвимостей и их реализаций. Формально, задача классификации состоит в создании системы категорирования, а именно, — в выделении категорий и создании классификационной схемы, как способа отнесения элемента классификации к категории.
При использовании заданной терминологии, неизбежно возникают разночтения между понятиями классификация и классификационная схема. Для устранения данного недостатка, в дальнейшем, используется термин «таксономия». Данный термин имеет греческое происхождение: от слов taxis — порядок и nomos — закон.
Таксономия — это «классификационная схема, которая разделяет совокупность знаний и определяет взаимосвязь частей». Ярким примером таксономий является таксономия растений и животных Карла Линнея.
В области защиты информации выделяют три группы таксономий:
К проблеме классификации атак имеется несколько подходов. Классически атаки разделяют на категории в зависимости от производимого эффекта,:
— нарушение конфиденциальности информации;
— нарушение целостности информации;
— отказ в обслуживании (нарушение доступности информации).
Главным недостатком подобной классификации является слабая информативность (а, следовательно, и применимость), так как по информации о классе атаки практически невозможно получить информацию об ее особенностях. Однако, эффект атаки является важным ее свойством и данный параметр в том или ином виде применяется в ряде таксономий (,,).
Другим подходом к классификации является классификация уязвимостей аппаратного и программного обеспечения информационно—вычислительных и телекоммуникационных систем. Одним из первых исследований в этом направлении является работа Атанасио, Маркштейна и Филлипса. Частично деление по типу уязвимости было использовано Ховардом и Лонгстаффом. Далее этот подход получил продолжение, которое в результате предлагает исследователям достаточно подробную классификация уязвимостей. Однако данный подход является слишком узким и зачастую не отражает в должной мере специфику атаки, поэтому применяется, в основном, лишь для специальных классов задач (при тестировании программного обеспечения и др.).
Другим возможным вариантом классификации является деление на основе начального доступа, которым обладает атакующий. Примером подобного подхода является матрица Андерсона. В своей работе Джеймс Андерсон (James P. Anderson) предложил основу классификации как наличие или отсутствие возможности доступа, атакующего к вычислительной системе (ВС) или к ее компонентам. Таким образом, категория, к которой принадлежит атака, зависит от начальных привилегий атакующего. Таксономия Андерсона предлагает матрицу 2 на 2.
Из приведенной таблицы (таблица 1) можно сделать заключение, что все атаки разделяются на три категории. Ситуация, когда атакующий имеет право запуска или использования программы в отсутствии доступа к вычислительной системе, — невозможен.
Таблица 1 — Матрица таксономии Андерсона
Категория B подразделяется Андерсоном дополнительно на три подкатегории. Следовательно, полный список категорий атак имеет следующий вид:
— Masquerader — ложный пользователь.
— Legitimate user — легальный пользователь.
— Clandestine user — скрытый пользователь.
Главным отличием между ложным, легальным и скрытым пользователями заключается в том, что ложный пользователь маскируется под легального пользователя, и, с точки зрения вычислительной системы, неотличим от него. Скрытый пользователь ориентируется на работу с вычислительной системой, при которой он остается незамеченным для систем обнаружения вторжений.
Рассматривая развитие классификационных подходов во времени, можно заметить, что ряд исследователей старались абстрагироваться от свойств состава атак, с целью создания общего списка типов атак. Наиболее известны в данном направлении работы Ноймана и Паркера. Аналогичную цель преследовал в своей работе Саймоном Хансмэном. Важным достоинством данного подхода является прикладная составляющая, так как в большинстве случаев информация о специфики атаки дает существенно больше, нежели знание каких—либо ее свойств. Однако недостатком данного подхода является наличие сильно пересекающихся категорий атак, а полнота классов зачастую недостижима.
В своей работе, П. Нойман и Д. Паркер представили 9 категорий способов вторжений (табл. 2).
Таблица 2 — Категории способов вторжения
На основе данных категорий П. Нойман разработал 26 видов атак (табл. 3)
Таблица 3 — Виды атак
В силу необходимости практической применимости таксономий, наиболее выгодными считаются комбинированные подходы, которые в некоторой степени реализуют все вышеописанные методы. Однако, способы комбинирования методов могут быть различны.
Один из способов комбинирования приводится в своей работе Саймон Хэнсмэн, — все анализируемые параметры разносятся отдельно и считаются попарно некоррелированными. Для достижения данной цели, автор использует концепцию «измерений», которая впервые была применена в работе Бишопа о классификации уязвимостей UNIX—систем.
Главную цель, которую преследовал Саймон Хэнсмэн, была разработка «прагматичной таксономии, которая полезна при ведении непрерывной работе над атаками». Первоначально производилась разработка таксономии древовидной структуры, подобно классификациям природного царства, — более общие категории находятся выше по высоте дерева, а нижние по высоте представляют более подробное описание категорий. Но на практике, в применении подобных классификационных схем имеется ряд неудобств. Во—первых, атаки зачастую несут смешанный характер. То есть складывается ситуация, при которой одна атака тесно зависит от другой или вложена в нее. Данная проблема, с одной стороны, решается путем введения межузловых ссылочных дуг между вершинами дерева, то есть при заполнении классификационной схемы образуется нагруженный граф. Однако это неизбежно сводится к беспорядку в структуре и сложностям при классификации. С другой стороны, возможно введение рекурсивных деревьев, где каждый лист дерева также является деревом. Но данное решение также сводится к беспорядочному росту структуры, и ограничению их применения. Во—вторых, атаки, в отличие от животных, не имеют обширного числа общих черт, вследствие чего имеют место сложности в формулировке классификационных групп верхних уровней. Действительно, у вредоносных программ типа «черви» или «вирусы» имеется достаточного много общих черт, однако непосредственных аналогий с атаками типа DoS (Denial of Service — отказ в обслуживании) и троянскими программами у них немного. Данная проблема ведет к разрастанию дерева на некоторое количество несвязанных между собой категорий, то есть до леса. Таким образом, древовидные классификации для практических задач.
Иной подход к созданию таксономий заключается в виде использования списочных структур. Таксономии, основанные на списочных структурах, представляются как совокупность списков категорий атак. С одной стороны, возможна организация общих классов категорий атак, с другой — возможно создание объемного количества списков, каждый из которых детально описывает уникальный класс категорий. Данные подходы также слабо применяются на практике, так как для первого случая организуются наборы крайне обобщенных категорий атак, а во—втором случае, детализация списков категорий бесконечна.
В предлагаемой Саймоном Хэнсмэном таксономии используется иной подход, основанный на концепции «измерений» Бишопа. Введение «измерений» позволяет комплексно рассматривать каждую атаку отдельно. В таксономии рассматривается четыре измерения для классификации атак:
1. Первое (базовое) измерение используется для категорирования атаки относительно классов атак на основе вектора атаки. Под вектором атаки понимается метод, с помощью которого атака достигает своей цели. При отсутствии подходящего вектора, атака классифицируется в ближайшую по смыслу категорию (табл. 4).
Таблица 4 — Значения вектора атак таксономии
Хэнсмэна по уровням детализации
2. Вторым измерением, атака классифицируется по цели атаки. Степень детализированности измерения достигается указанием конкретной версии продукта, например Linux Kernel 3.5.1rc—1, или же покрывается определенным классом возможных целей, например Linux Kernel (табл. 5).
Таблица 5 — Список целей атак таксономии
Хэнсмэна по уровням детализации
3. Третье измерение используется для описания уязвимостей и эксплоитов, которыми реализуется данная атака. Измерение представляется списоком номеров CVE (Common Vulnerabilities and Exposures) известных уязвимостей по классификации проекта CVE [12].
Идея проекта CVE была предложена Мэнном (Mann) и Кристли (Christley) [24] и предлагает унифицированный способ представления определений уязвимостей. На данный момент, проект является стандартом де—факто описания уязвимостей, и его применение является желательным в таксономиях прикладного направления.
Дополнительно, в таксономии Хэнсмэна предполагается ситуация, когда на момент классификации атаки не существует ее описания (CVE—номера) уязвимости. В этом случае, предлагается использовать общие классы категорий атак процессной таксономией компьютерных и сетевых атак Ховарда [13], — уязвимость в реализации (логические ошибки в текстах программ), уязвимость в проекте, уязвимость в конфигурации. В данной таксономии рассматривается в качестве центрального понятия инцидент — совокупность атакующего, атаки и цели атаки. Главным ее отличием является наличие структурных элементов: инцидентов и события, — совокупности действия и целевого объекта. Предусматривается возможность комбинирования событий. Таким образом, в инциденте возможно вложение последовательность атак. Полезным свойством таксономии Ховарда является возможность описания неатомарных (составных) атак и учет их сценариев проведения. Однако, как указывается в тезисах докторской диссертации Лауфа, процессная таксономия привносит двусмысленность при классификации атаки на практике, так как нарушается свойство взаимного исключения.
4. Четвертое измерение используется для классификации атаки по наличию и виду полезной нагрузки (payload) или реализуемого эффекта. В большинстве случаев, в результате своей работы, с атакой привносится дополнительный эффект. Например, «вирус», используемый для установки потайного входа (backdoor) очевидно остается «вирусом», но несет в качестве полезной нагрузки программу потайного входа.
В качестве классов категорий полезной нагрузки, Хэнсмэн выделяет:
— Полезная нагрузка первого измерения — собственно полезная нагрузка является атакой;
— Кража сервиса (подмена сервиса);
— Subversion — полезная нагрузка предоставляет контроль над частью ресурсов цели и использует их в своих целях.
В 1995 году, Бишоп [10] предложил классификацию относительно уязвимостей для UNIX—систем. Отличительная особенность его работы заключается в создании принципиально новый схемы классификации. Шесть «осей координат» представляются компонентами [7], [10]:
— Природа уязвимости — описывается природа ошибки в категориях протекционного анализа;
— Время появления уязвимости;
— Область применения — что может быть получено через уязвимость;
— Область воздействия — на что может повлиять уязвимость;
— Минимальное количество — минимальное количество этапов, необходимых для атаки;
— Источник — источник идентификации уязвимости.
Особенностью классификации Бишопа является использование подхода на основе концепции измерений, вместо табличных и древовидных классификаций. Каждая координатная ось представляется классификационной группой, отсчеты по которой являются элементы группы, а уязвимость описывается в виде некоторой точке в «пространстве» координатных осей. Данная схема именуется таксономией уязвимостей в концепции измерений. Таксономия Бишопа является ярким представителем групп таксономий уязвимостей.
Важной основой для разработки новых таксономий уязвимостей в области информационной безопасности послужили работы Бисби (Bisbey) и Холлингворса (Hollingworth), посвященные протекционному анализу [25], а также работы по исследованию защищенных операционных систем (RI SOS) Аббота (Abbott), Вебба (Webb) и др. [4]. Обе таксономии фокусируют внимание на классифицировании ошибок в программном обеспечении и приблизительно схожи между собой.
Непригодность практического применения таксономий [25], [4] в своей дальнейшей работе описали Бишоп и Бэйли [11]. Проблемой предложенных таксономии является двусмысленность в определениях своих классов, то есть в определениях нескольких классов некоторые уязвимости равносильны, что приводит к нарушению правила взаимоисключения между классами, и тем самым представляются малопригодными в прикладном смысле. Однако, данные работы [25], [4] заложили основу ценным концепциям, которые получили свое развитие в последующих исследованиях [10], [26], [].
Комбинированный подход к классификации уязвимостей прослеживается и в нормативно—распорядительной документации ФСТЭК России. В классификации уязвимостей, предлагаемой базовой моделью угроз ИСПДн (рисунок 1), также применяется комбинированный подход, основанный на идеях работ Ховарда, Хэнсмэна, Бишопа и др.
Более того, для систематизации уязвимостей в соответствии с классификацией на практике, в документах предлагается использовать существующие зарубежные базы данных (БД) уязвимостей в качестве источников информации. Наиболее распространенной базой данных об уязвимостях является БД National Vulnerability Database (NVD), которая основывается на объединении информации из более ранних баз данных (CPE, CVE, и др.)
1.3 Математические модели систем защиты информации
В работе [23] рассматривается вероятностная модель, в которой система защиты информации (СЗИ) представлена неконтролируемыми преградами вокруг предмета защиты. В общем случае модель элементарной защиты предмета может быть в виде защитных колец (рисунок 2). В качестве предмета защиты выступает один из компонентов информационной системы (ИС).
Рисунок 2 — Модель элементарной защиты
Вероятность невозможности преодоления преграды нарушителем обозначается как Рсзи, вероятность преодоления преграды нарушителем через Рнр соответственно сумма вероятностей двух противоположных событий равна единице, то есть:
В модели рассматриваются пути обхода преграды. Вероятность обхода преграды нарушителем обозначается через Робх, которое представляется в виде:
В случае, когда у преграды несколько путей обхода:
где — k количество путей отхода.
Для случая, когда нарушителей более одного, и они действуют одновременно (организованная группа) по каждому пути, это выражение с учетом совместности событий выглядит как:
Учитывая, что на практике в большинстве случаев защитный контур (оболочка) состоит из нескольких «соединенных» между собой преград с различной прочностью, рассматривается модель многозвенной защиты (рисунок 3).
Выражение прочности многозвенной защиты из неконтролируемых преград, построенной для противостояния одному нарушителю, представлено в виде:
где — Рсзи прочность i—й преграды, Робх — вероятность обхода преграды по k — му пути.
Рисунок 3 — Модель многозвенной защиты
Выражение для прочности многозвенной защиты, построенной из неконтролируемых преград для защиты от организованной группы квалифицированных нарушителей—профессионалов, с учетом совместности событий представляется в виде:
В случае, когда какие—либо преграды дублируются, а их прочности равны соответственно Р1,Р2,Р3,…,Рi то вероятность преодоления каждой из них нарушителем соответственно равна (1 — Р1), (1 — Р2), (1 — Р3),…, (1 — Рi).
Учитывая, что факты преодоления этих преград нарушителем события совместные, вероятность преодоления суммарной преграды нарушителем формально представляется в виде:
Вероятность невозможности преодоления дублирующих преград (прочность суммарной преграды) как противоположное событие определяется выражением:
где — i порядковый номер преграды, Pi прочность i — й преграды.
Также в работе представлена модель многоуровневой системы защиты (рисунок 4).
Рисунок 4 — Модель многоуровневой защиты
При расчете суммарной прочности нескольких оболочек (контуров) защиты в формулу (7) вместо Pi, включается Pki — прочность каждой оболочки (контура), значение которой определяется по одной из формул (4), (5) и (6):
При Pki = 0 данная оболочка (контур) в расчет не принимается. При Pki = 1, остальные оболочки защиты являются избыточными. Данная модель справедлива лишь для замкнутых оболочек защиты, перекрывающих одни и те же каналы несанкционированного доступа к одному и тому же предмету защиты.
В случае контролируемой преграды, т.е. когда преграда связана с каким—либо тревожным датчиком, который может подать сигнал в случае попытки преодоления преграды.
Исходя из данной временной диаграммы процесса контроля и обнаружения несанкционированного доступа (НСД) (рисунок 5), в работе [27] приводятся формулы для расчета вероятности обнаружения и блокировки НСД Робл и Ротк вероятности отказа системы обнаружения:
где λ — интенсивность отказов группы технических средств, составляющих систему обнаружения и блокировки НСД, t — рассматриваемый интервал времени функционирования системы обнаружения и блокировки НСД.
Рисунок 5 — Временная диаграмма процесса контроля НСД
(T — период опроса датчиков; Tоб — время передачи сигнала и обнаружения НСД; Тбл — время блокировки доступа; Тобл — время обнаружения и блокировки; — время простоя)
Учитывая, что отказ системы контроля и НСД могут быть совместными событиями, формула прочности контролируемой преграды для элементарной защиты принимает вид:
где Робл и Ротк определяются соответственно по формулам (9) и (10), Робх и количество путей обхода к определяются экспертным путем на основе анализа принципов построения конкретной системы контроля и блокировки НСД.
Выражение для прочности многозвенной защиты с контролируемыми преградами для защиты от одного нарушителя будет в следующем виде
где Рсзиkn прочность n—й преграды, Робхn — вероятность обхода преграды по j — му пути.
Формула для расчета прочности защитной оболочки с контролируемыми преградами для защиты от организованной группы нарушителей представлена в виде:
В работе [28] приводится вероятностная модель оценки уязвимости информации. В данной модели выделяется пять зон, в которых возможны несанкционированные действия:
Источник






























