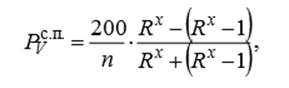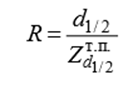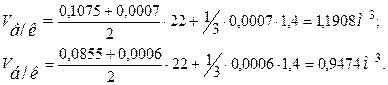- 51. Физические и математические способы определения объема стволов. Приближенные способы определения объема растущих деревьев.
- 52. Классификация лесоматериалов и методы их таксации (в плотной и складочной мерах).
- Исследование таксационных показателей срубленного дерева. Математические способы определения объема дерева
- Страницы работы
- Фрагмент текста работы
- Таксация срубленного дерева 1 страница
51. Физические и математические способы определения объема стволов. Приближенные способы определения объема растущих деревьев.
Объем ствола срубленного дерева и его части можно определить физич. и математ. методами.
физич.методы – Ксилометрический (основан на законе Архимеда, по объёму вытесненной жидкости, с постоянным и переменным уровнем) и весовой (при нем V древесины опр-ся делением ее массы на плотность, которая зависит от породы и влажности). Используют гидростатические весы – вес в воздухе и вес в воде.
Математич.способ основаны на стереометрии. Основные объемообразующ. Показатели (Д,h и формы ствола) зависят от множества факторов (порода, А, усл.роста). Исходя из того, что ствол правильное тело вращения формулы для исчисления не сложны. Поэтому при определении объема древесного ствола его форму нередко сравнивают с правильными телами вращения, формулы которых уже известны: цилиндра (V=g0*h) , конусом(V=g0*h/3) , параболоидом (V=g0*h/2) , и нейлоидом (V=g0*h/4). Сделав сечение примерно на границе перехода одной части образующей в другую, получим фигуры: в нижней части ствола усеченный нейлоид, в средней – цилиндры, выше половины высоты – усеченный параболоид, вершинка –конусу.
Определение объема ствола растущего дерева вычисляют по формуле Vc=g1,3*h*f. Для этой формулы площадь сечения определяют по измеренному диаметру на высоте груди, а видовое число берут из таблицы видовых чисел.
Способ Денцена Vs=d 2 1,3/1000. Для определения – измеряют диаметр на высоте груди в целых сантиметрах, возводят его в квадрат, отделяют три десятичных знака справа и получают объем в кубометрах.
52. Классификация лесоматериалов и методы их таксации (в плотной и складочной мерах).
Сортименты – виды лесной продукции.
1.деловые – используется в круглом виде и используется для дальнейшей переработки.
2.дровяные – используется для отопления, углежжения, сухой перегонки. Таксация дров, учет в поленницах Vскл=a*l*h, Vпл=Vскл*Кт
Деловые сортименты делятся на: обработанные и круглые.
Лесоматериалы по способу получении и характеру обработки делятся на:
круглые л/м сохранившие форму боковой поверхности ствола (пиловочные и строительные бревна, руд.стойка, балансы. Из лиственных фанерный и спичечный кряж). Определение объема в плотной и складочной мере. Объем по формуле срединного сечения, существуют таблицы по D, L → V/ На практике определяется по табл. На основании длины и диаметра в верхнем отрезе, составленные для среднего сбега 1см на 1п.м.
дрова в круглом или колотом виде
пиломатериалы, полученные продольной распиловкой (пластина, четвертина, брусья, брусок, шпала, доска, горбыль, паркет)
Брусья – 2-х, 3-х, 4-х кантные по количеству пропиленных сторон. Больше 10см размеры.
л/м из корневых и прикорневых частей (осмол, болванки)
л/м из коры древ. И куст. пород
Объем хлыстов – производят перечет хлыстов по градациям толщины на 1,3м от комля, затем для 15-20 хлыстов находим, на основе вспомогательной таблице определяем разряд высот, из таблицы объема хлыстов соот. разряда выписываем объем одного хлыста для каждой категории толщины и находим хлыст + объем хлыста штабеля.
Учет круглого леса в склад.мере. Vшт=l*h*a.
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.
Источник
Исследование таксационных показателей срубленного дерева. Математические способы определения объема дерева
Страницы работы
Фрагмент текста работы
Вопросы и ответы к защите первой работы – исследование таксационных показателей срубленного дерева:
1. Что лежит в основе математических способов определения объема срубленного дерева?
Расчет объема ствола срубленного дерева математическими способами, в порядке уменьшения точности, производится по:
Сложной формуле срединного сечения Губера (3.1);
Ствол разделяют на секции: длиной 2 м, если высота ствола превышает 15 м; длиной 1м – при высоте от 8 до 15 м; длиной 0,5 м – при высоте менее 8 м. Число секций должно быть не менее 10. Объем ствола по сложной формуле Губера определяется как сумма объемов всех секций и объема вершины.
Простой формуле двух сечений Гаусс-Симони (3.8);
Простой формуле срединного сечения – формула Губера (3.7).
Для того, чтобы вычислить объем ствола по формулам 3.7 и 3.8, сначала необходимо определить диаметры ствола на высотах 0,5h; 0,2h; 0,8h.
2. Назовите математические способы определения объема дерева.
— Сложная формула срединного сечения Губера
— Простая формула двух сечений Гаусс-Симони
— Простая формула срединного сечения – формула Губера
3. Какой из способов дает наименьшую погрешность в определении объема ство- ла срубленного дерева?
— Сложная формула срединного сечения Губера
4. Что такое абсолютный сбег ствола?
—Абсолютный действительный сбег – это два ряда чисел показывающих изменение диаметра ствола (di, см) с изменением высоты сечения (hi, м). Это основной показатель древесного ствола.
5. Показатели относительного сбега.
6. Чем характеризуется полнодревестность ствола?
—Старым видовым числом (fc), показывающим, какую часть объема равновеликого цилиндра составляет ствол
7. Что такое видовое число?
8. Как изменяется значение видового числа с увеличением возраста дерева?
9. Назовите критерии разделки ствола на сортименты.
10. Какая часть ствола относится к деловой?
—Все, кроме вершинной части, и участка ствола, идущего на дрова
Что представляет собой ликвидная древесина?
—Ликвидная древесина – делится на дровяную, имеющую диаметр в верхнем отрезе в коре 3 см и более, и деловую, диаметр которой в верхнем отрезе без коры больше 6 см.
Из чего образуется отходы древесного ствола?
— Из вершинной части дерева
Вопросы и ответы к защите второй работы – Исследование прироста дерева:
1. Что такое прирост дерева?
— Прирост (ZT) – изменение таксационного показателя дерева (Т) с изменением его возраста (А).
2. Назовите виды приростов для отдельного дерева.
— Текущий прирост – разность абсолютных значений любого таксационного показателя за определенный промежуток времени.
Различают три вида текущего прироста:
А.) Текущий общий, показывающий изменение таксационного показателя за всю жизнь дерева:
Б.) Текущий периодический, показывающий изменение таксационного показателя за определенный период времени
В.) Текущий годичный, определяемый за один год
— Средний прирост – среднее изменение таксационного показателя за наблюдаемый период.
Различают следующие виды среднего прироста:
-средний общий – средняя скорость изменения таксационного показателя за весь период жизни дерева
-средний периодический – средняя скорость изменения таксационного показателя за наблюдаемый период
3. С какой целью приросты рассчитывают в процентах?
—Темп прироста свидетельствует об относительном приросте. Это величина относительная и вычисляется в процентах или долях, как коэффициент прироста.
4. Как определяется возраст количественной спелости?
—Возраст количественной спелости определяют по максимуму среднего прироста (изменение запаса) древостоя.
5. Назовите способы определения процента среднего периодического прироста по объему?
— Процент среднего периодического прироста определяют по формуле Пресслера
6. В чем заключается приближение при определении процента среднего периодического прироста объема по простой формуле?
7. Как рассчитывается относительный диаметр для растущего и для срубленного дерева?
Для растущего дерева
Для срубленного дерева процент прироста по объему находится по относительному диаметру на ½ высоты дерева
8. От чего зависит коэффициент К в формуле Шнейдера?
— K – коэффициент, зависящий от интенсивности роста и протяженности кроны дерева
Вопросы и ответы к защите третьей работы — ТАКСАЦИЯ СОВОКУПНОСТИ
Источник
Таксация срубленного дерева 1 страница
Ствол срубленного дерева является одним из главных объектов таксации, так как в нем сосредоточена основная доля древесной массы, к тому же имеющая наибольшее хозяйственное значение.
Применяемые методы таксации можно разделить на физический (который включает в себя ксилометрический и весовой способы) и стереометрический. Ксилометрический способ таксации базируется на законе Архимеда, который гласит: “Тело, погруженное в жидкость, вытесняет объем жидкости, равный объему тела”.
Приборы для определения объема частей древесных стволов (т.к. единовременное определение объемов стволов целиком невозможно в силу их значительных размеров) называют “ксилометрами”. Использование этих приборов позволяет с относительно высокой точностью определить объем древесных отрубков, а затем, суммируя их, переходить к объему ствола. Для повышения точности оценки иногда в качестве наполнителя применятся ртуть (прибор называется ртутным ксилометром), которая в отличие от воды не впитывается в поры древесины. Весовой способ используется в основном для учета лесоматериалов круглых (бревен), то есть частей древесных стволов, и описан ниже в соответствующем разделе. При таксации стволов срубленных деревьев наиболее применим стереометрический метод таксации. Данный метод следует считать приближенным, т.к. при его использовании заведомо допускаются искажения истинной, очень сложной и индивидуальной формы древесных стволов, которая условно приравнивается к форме правильного тела вращения или совокупности таких тел.
Те стереометрические формулы, которые позволяют определить объем ствола в целом, называют простыми, а формулы, в которых объем ствола определяют по отдельным частям (секциям), называют сложными.
Из простых формул наиболее часто употребляют для определения объема ствола и его частей формулы срединного и среднего сечения. Формула срединного сечения (или формула Губера) названа так потому, что площадь сечения для определения объема берется на средине длины ствола (или его отрезка) и умножается на длину ствола.
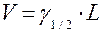
где V – объём ствола, м 3 ;
γ1/2– площадь поперечного сечения на средине ствола, м 2 ;
L – длина ствола, м.
Для определения объема ствола с помощью формулы срединного сечения достаточно длину (высоту) ствола умножить на площадь сечения на половине длины (высоты). Нужно только оба множителя предварительно перевести в одинаковую размерность (метры или сантиметры).
В формуле среднего сечения используют среднее значение из площади сечений основания и основания вершины ствола (формула усеченного параболоида):
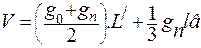
где g0 – площадь сечения основания ствола, м 2 ;
gn – площадь сечения основания вершины, м 2 ;
L / — длина ствола без вершины, м ;
Эта формула известна под названием формулы Смалиана, точнее будет ее назвать формулой объема “по среднему диаметру”. Поскольку у основания дерево имеет обычно утолщение и наплывы, то для целых стволов эта формула дает значительные преувеличения объема.
Были предложены еще многие формулы определения объема ствола по нескольким (двум или трем) сечениям, но более надежным признавалось их вычисление секционными способами.
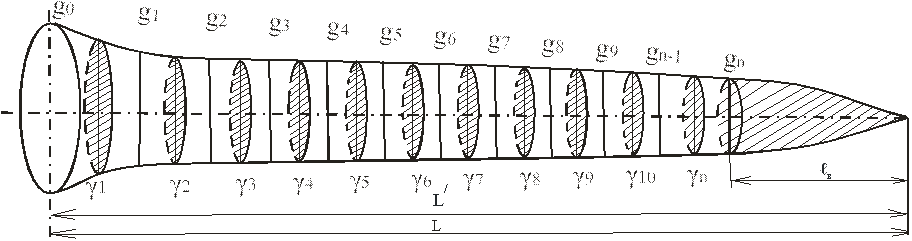
Их применение требует разделение ствола на части (секции), к которым с большим правом можно применять сравнение с цилиндром. Если обозначить площади сечений ствола на границах n секций, на которые разделен ствол, через g0, g1 , g2, ….. g n -1, g n и посередине этих секций – через g1, g2 . gn, длину секции через l,а длину вершины через lв, то объем ствола по сложной формуле среднего сечения выразится уравнением
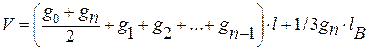
Для сложной формулы срединного сечения получим выражение
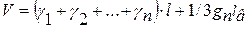
Общепринято деление ствола при определении его объема на одно – или двухметровые секции (в зависимости от его высоты), но в последние годы часто применяли деление на десять секций равной длины.
1. Составление таблицы исходных данных
Для выполнения расчетной работы используются данные базового варианта, приведенные в таблице 2.
Таблица 2 — Исходные данные для выполнения расчетной части
| Месторасположение дерева | |
| 1. Край Красноярский | 2. Лесничество Усть-Ангарское |
| 3. Участковое лесничество Южно-Енисейское | 4. Квартал 73, выдел 5, пробная площадь № 060-5 |
| 5. Состав насаждения 10С | 6. Возраст насаждения 90 лет |
| 7. Полнота 1.0 | 8. Бонитет III |
| 9. Класс товарности 1 | 10. Покров: з. мхи, брусника |
| 11. Почва: суглинистая свежая | 12. Положение: пологий южный склон |
| Характеристика ствола | |
| 13. Порода: сосна | 14. Диаметр на 1,3 м — 33,1 см |
| 15. Высота дерева — 23,4 м | 16. Возраст дерева — 92 года |
| 17. Класс морфологического развития – 1 | 18. Объем ствола в коре — 0,9358 м 3 |
| 19. Объем ствола без коры – 0,8507 м 3 | 20.Объем ствола 10 лет назад-0,6555м 3 |
| 21. Объем коры ствола — 0,0851 м 3 | 22. Видовое число в коре — 0,465 |
Продолжение таблицы 2
| 23. Видовое число без коры – 0,539 | |
| 24. Коэффициенты формы | 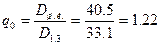 ; ; 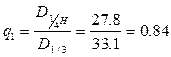 ; ; 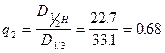 ; ; 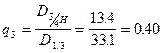 . . |
| 25. Классы формы | 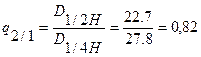 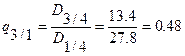 |
Продолжение таблицы 2
| № секции | Высота от пня, м | Диаметр, см | Объем, м 3 | Порок | |||
| в коре | без коры | 10 лет назад | в коре | без коры | 10 лет назад | ||
| шейка корня | 40,5 | 35,7 | — | — | — | — | — |
| пень | 37,0 | 33,0 | — | — | — | — | — |
| высота груди | 33,1 | 29,3 | 26,0 | — | — | — | — |
| I | 33,5 | 30,7 | 27,4 | 0,1763 | 0,1480 | 0,1179 | — |
| II | 30,5 | 28,4 | 25,9 | 0,1461 | 0,1267 | 0,1054 | — |
| III | 28,4 | 27,1 | 24,6 | 0,1267 | 0,1154 | 0,0951 | — |
| IV | 27,0 | 26,1 | 23,7 | 0,1145 | 0,1070 | 0,0882 | — |
| V | 25,9 | 25,2 | 22,4 | 0,1054 | 0,0998 | 0,0788 | — |
| VI | 23,5 | 23,0 | 20,2 | 0,0867 | 0,0831 | 0,0641 | с 11 метра |
| VII | 21,2 | 20,7 | 17,5 | 0,0706 | 0,0673 | 0,0481 | до 22 метра сучки |
| VIII | 18,2 | 17,8 | 14,4 | 0,0620 | 0,0498 | 0,0326 | диаметром 6 см |
Окончание таблицы 2
| № секции | Высота от пня, м | Диаметр, см | Объем, м 3 | Порок | |||
| в коре | без коры | 10 лет назад | в коре | без коры | 10 лет назад | ||
| IX | 14,4 | 14,0 | 10,4 | 0,0326 | 0,0308 | 0,0170 | — |
| X | 10,9 | 10,5 | 6,8 | 0,0187 | 0,0173 | 0,0073 | — |
| XI | 6,1 | 5,8 | 2,5 | 0,0058 | 0,0053 | 0,0010 | |
| Основание вершинки | 3,0 | 2,7 | — | 0,00033 | 0,00027 | — | — |
| Объем ствола по сложной формуле Губера | 0,9358 | 0,8507 | 0,6555 | — | |||
| Объем цилиндра V = g1,3* Н | 2,0136 | 1,5778 | — | — |
Базовый вариант является основой для выполнения работы всеми студентами. Чтобы трансформировать базовый вариант в индивидуальное задание, необходимо воспользоваться таблицей 3.
Таблица 3 – Поправки для формирования вариантов заданий по лабораторным работам, на которые необходимо увеличить диаметры дерева и длину вершины
| Последняя цифра номера зачет ной книжки | Первая буква фамилии | |||||
| А, Ж, Н, У, Щ | Б З, О, Ф, Ы | В, И, П, Х,Э | Г, К, Р, Ц, Ю | Д, Л, С, Ч, Я | Е, М, Т, Ш | |
| 0,1 | 1,1 | 2,1 | 3,1 | 4,1 | 5,1 | |
| 0,2 | 1,2 | 2,2 | 3,2 | 4,2 | 5,2 | |
| 0,3 | 1,3 | 2,3 | 3,3 | 4,3 | 5,3 | |
| 0,4 | 1,4 | 2,4 | 3,4 | 4,4 | 5,4 | |
| 0,5 | 1,5 | 2,5 | 3,5 | 4,5 | 5,5 | |
| 0,6 | 1,6 | 2,6 | 3,6 | 4,6 | 5,6 | |
| 0,7 | 1,7 | 2,7 | 3,7 | 4,7 | 5,7 | |
| 0,8 | 1,8 | 2,8 | 3,8 | 4,8 | 5,8 | |
| 0,9 | 1,9 | 2,9 | 3,9 | 4,9 | 5,9 | |
| 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | |
| Поправка на длину вершины, м | 0,5 | 1,0 | 1,5 | 2,0 | 2,5 | 3,0 |
Величина поправки для индивидуального задания определяется по первой букве фамилии и последней цифре номера зачетной книжки. Диаметры дерева, обмеренные в различных частях, должны быть увеличены на поправку, находящуюся на пересечении первой буквы фамилии и последней цифры номера зачетной книжки. По первой букве фамилии увеличивается длина вершины. Запись данных индивидуального варианта производится в форму (таблицы 2). Например: у студента Иванова номер зачетной книжки 027013. Как видно, что последней цифрой номера является «3», а первой буквой фамилии «И». В таблице 2 в первом столбце находится цифра «3» , а первая буква фамилии «И» в четвертом столбце. Таким образом, на пересечении цифры «3» и буквы «И»искомая поправка к диаметрам обмеренных в различных частях древесного ствола составит – 2,4 см. Поправка на длину вершины находится по первой букве фамилии «И», следовательно, она составит – 1,5 м.
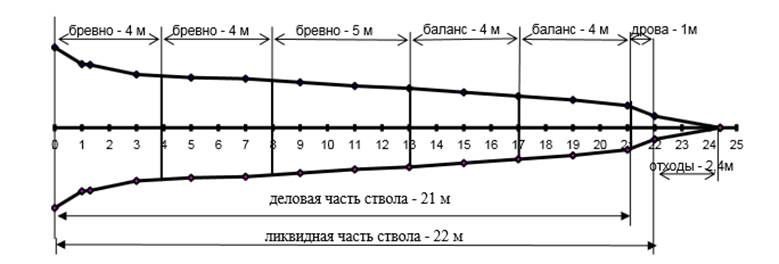
2. Вычерчивание схематического продольного разреза ствола с разделением на двухметровые секции (рисунок 1).
3.Вычисление объема древесного ствола по простым стереометрическим формулам.
а) Вычисление объема по простой формуле Губера ( формула 1).
Для базового варианта L = 23, 4 м, а половина длины равна 11, 7 м, т.е необходимо найти диаметр на расстоянии 11, 7 м от комлевого среза (от пня). В таблице 2 имеются обмеры диаметров ствола на 11 метре и 13 метре : D11 = 23,5 см; D13 = 21,2 см, диаметр на расстоянии 11.7 находится методом интерполирования. Сначала определяется изменение диаметра, приходящееся на 2 м длины, т.е. от 11 ого до 13 ого метра D11 — D13 = 23,5 — 21,2 = 2,3 см, а затем изменение диаметра, приходящееся на 0,7 м от 11 до 11, 7 метра, по пропорции:
на 2 м изменение составляет 2,3 см;
на 0,7 м изменение составляет X см,
отсюда 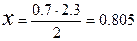
Следовательно, диаметр на 1/2 L будет равен
D11,7 = D11 – X = 23,5 — 0,8 = 22,7 см.
По приложению А находится площадь поперечного сечения на середине древесного ствола (g1/2L) и по формуле (1) определяется объем ствола. Для базового варианта
Vв.к. = 0,0404 · 23,4 = 0,9454 м 3 ;
Vб.к. = 0,0387 · 23,4 = 0,9056 м 3 .
Площадь поперечного сечения также можно определить по формуле
Рисунок 1 – Схематический продольный разрез древесного ствола
б) Вычисление объема по простой формуле среднего сечения (простая формула Смалиана, формула (2))
Площади сечения g0, … gn в м 2 определяются с использованием таблицы приложения А по D0 и Dn.
D0 = 37,0 см; g0 = 0,1075 м 2 ; Dn = 3,0 см; gn = 0,0007 м 2 ;
4.Определение объема древесного ствола по сложным стереометрическим формулам:
а) сложная формула срединного сечения (сложная формула Губера, формула (4)).
Объемы 2 метровых секций определяются по таблице приложения Б по диаметрам на нечетных метрах (колонки 3, 4, 5) и записываются в таблицу 2 (колонки 6, 7, 8). Объем вершины записывается напротив четного метра. Сумма объемов двухметровых секций и объема вершины дает объем ствола в коре, без коры и 10 лет назад.
б) Сложная формула средних сечений (сложная формула Смалиана, формула (3)).
Диаметры на четных метрах определяются как среднеарифметические между двумя диаметрами на нечетных метрах, например: диаметр на втором метре определится следующим образом:
d2 = 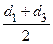
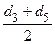
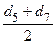
Для более компактной записи результатов по определению объема ствола по сложной формуле Смалиана предлагается таблица 4, в которую необходимо занести вычисленные диаметры на четных метрах. По этим диаметрам (в коре и без коры) определяются площади поперечных сечений (приложение А) и рассчитываются объемы двухметровых секций, сумма которых с объемом вершины дает объем ствола в коре и без коры.
Таблица 4 – Вспомогательная таблица
| Высота, м | Диаметр, см | Площадь сечения, м 2 | Объем, м 3 | ||
| в коре | без коры | в коре | без коры | в коре | без коры |
| 37,0 | 33,0 | 0,1075 | 0,0855 | — | — |
| 32,0 | 29,6 | 0,0804 | 0,0686 | 0,1879 | 0,1541 |
| 29,5 | 27,8 | 0,0681 | 0,0605 | 0,1485 | 0,1291 |
| 27,7 | 26,6 | 0,0603 | 0,0556 | 0,1284 | 0,1161 |
| 26,5 | 25,7 | 0,0549 | 0,0517 | 0,1152 | 0,1072 |
| 24,7 | 24,1 | 0,0479 | 0,0456 | 0,1029 | 0,0973 |
| 22,4 | 21,9 | 0,0392 | 0,0375 | 0,0871 | 0,0831 |
| 19,7 | 19,3 | 0,0305 | 0,0291 | 0,0697 | 0,0666 |
| 16,3 | 15,9 | 0,0209 | 0,0199 | 0,0513 | 0,0490 |
| 12,7 | 12,3 | 0,0126 | 0,0118 | 0,0334 | 0,0316 |
| 8,5 | 8,2 | 0,0057 | 0,0052 | 0,0182 | 0,0170 |
| 3,0 | 2,7 | 0,0007 | 0,0006 | 0,0064 | 0,0058 |
| ∑V n | 0,9492 | 0,8569 | |||
| Vв в/к = 0,333 · 0,0007 · 1,4 = 0,00033 Vв б/к = 0,333 · 0,0006 · 1,4 = 0,00028 | 0,0003 | 0,00027 | |||
| V ствола = ∑ V n + V в | 0,9495 | 0,8572 |
В данном примере запись по определению объема ствола в соответствии с формулой (3) будет следующей:
Vств в/к = (0,1075+0,0804)+(0,0804+0,0681)+(0,0681+0,0603)+(0,0603+0,0549)+
(0,0549+0,0479)+(0,0479+0,0392)+(0,0392+0,0305)+(0,0305+0,0209)+(0,0209+0,0126)+(0,0126+0,0057)+(0,0057+0,0007)+0,0003= 0,9495 м 3 .
Как видно из данного выражения, что сумма площадей сечений на нулевом срезе и втором метре дает объем первой двухметровой секции, а также и сумма площадей сечений на втором и четвертом метрах объем второй секции и так на последующих метрах древесного ствола.
5. Производится сопоставления результатов вычислений объемов
ствола по различным формулам.
За истинное значения ствола по различным формулам принимают объем ствола, полученный по сложной формуле Губера. Данные заносятся в таблицу 4.
б) Вычисление объема по простой формуле среднего сечения (простая формула Смалиана, формула (2))
Площади сечения g0, … gn в м 2 определяются с использованием таблицы приложения А по D0 и Dn.
D0 = 37,0 см; g0 = 0,1075 м 2 ; Dn = 3,0 см; gn = 0,0007 м 2 ;
4.Определение объема древесного ствола по сложным стереометрическим формулам:
а) сложная формула срединного сечения (сложная формула Губера, формула (4)).
Объемы 2 метровых секций определяются по таблице приложения Б по диаметрам на нечетных метрах (колонки 3, 4, 5) и записываются в таблицу 2 (колонки 6, 7, 8). Объем вершины записывается напротив четного метра. Сумма объемов двухметровых секций и объема вершины дает объем ствола в коре, без коры и 10 лет назад.
б) Сложная формула средних сечений (сложная формула Смалиана, формула (3)).
Диаметры на четных метрах определяются как среднеарифметические между двумя диаметрами на нечетных метрах, например: диаметр на втором метре определится следующим образом:
d2 = 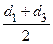
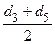
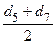
Для более компактной записи результатов по определению объема ствола по сложной формуле Смалиана предлагается таблица 4, в которую необходимо занести вычисленные диаметры на четных метрах. По этим диаметрам (в коре и без коры) определяются площади поперечных сечений (приложение А).
Таблица 4 – Вспомогательная таблица
| Высота, м | Диаметр, см | Площадь сечения, м 2 | |
| в коре | без коры | в коре | без коры |
| 37,0 | 33,0 | 0,1075 | 0,0855 |
| 32,0 | 29,6 | 0,0804 | 0,0686 |
| 29,5 | 27,8 | 0,0681 | 0,0605 |
| 27,7 | 26,6 | 0,0603 | 0,0556 |
| 26,5 | 25,7 | 0,0549 | 0,0517 |
| 24,7 | 24,1 | 0,0479 | 0,0456 |
| 22,4 | 21,9 | 0,0392 | 0,0375 |
| 19,7 | 19,3 | 0,0305 | 0,0291 |
| 16,3 | 15,9 | 0,0209 | 0,0199 |
| 12,7 | 12,3 | 0,0126 | 0,0118 |
| 8,5 | 8,2 | 0,0057 | 0,0052 |
| 3,0 | 2,7 | 0,0007 | 0,0006 |
По площадям поперечных сечений на концах 2 метровых отрезков (таблица 4) вычисляется объем ствола по сложной формуле среднего сечения (формула 3).
5. Производим сопоставление результатов вычислений объемов
ствола по различным формулам.
За истинное значения ствола по различным формулам принимают объем ствола, полученный по сложной формуле Губера. Данные заносятся в таблицу 5.
Ошибка в коре в данном примере будет вычислена следующим образом: ошибка в коре по сложной формуле среднего сечения = 0,9495 – 0,9358=0,0137 м 3 . В процентах ошибка составит = 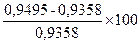
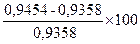
Таблица 5 — Результаты таксации срубленного дерева
| Формула | Объем, м 3 | Ошибка, м 3 | Ошибка, % | ||||
| в коре | без коры | объем коры | в коре | без коры | в коре | без коры | |
| Сложная срединного сечения | 0,9358 | 0,8507 | 0,0851 | — | — | — | — |
| Сложная среднего сечения | 0,9495 | 0,8572 | 0,0923 | 0,0137 | 0,0065 | 1,46 | 0,76 |
| Простая срединного сечения | 0,9454 | 0,9056 | 0,0398 | 0,0096 | 0,0549 | 1,03 | 6,45 |
| Простая среднего сечения | 1,1908 | 0,9474 | 0,2434 | 0,2550 | 0,0967 | 27,25 | 11,37 |
6. Делается заключение о точности определения объема ствола по применяемым формулам. Необходимо объяснить, за счет чего бывают большие отклонения.
2.1.2 Сортиментация древесного ствола и определение объемов сортиментов
Отдельные виды лесной продукции, получаемые в результате эксплуатации доминирующего ресурса, т.е. древесины (наряду с которым эксплуатации подвергаются и другие ресурсы леса), называются сортиментами.
Наиболее крупную и важную группу сортиментов представляют лесоматериалы круглые, которые могут использоваться в хозяйстве в необработанном виде и быть сырьем для дальнейшей обработки. Размеры, качество и назначение лесоматериалов круглых должны соответствовать требованиям государственных стандартов (ГОСТов). Базовыми стандартами следует считать ГОСТ 9463-88. Лесоматериалы круглые хвойных пород. Технические условия и ГОСТ 9462-88. Лесоматериалы круглые лиственных пород. Технические условия.
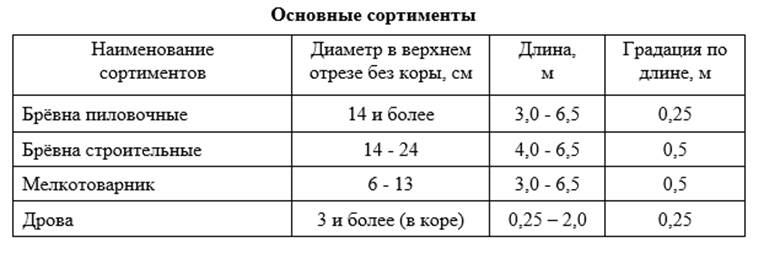
В зависимости от качества древесины лесоматериалы заготавливаются 1, 2 и 3 сортов. Категории крупности по толщине круглых лесоматериалов устанавливаются по тонкому торцу бревна (верхнему отрубу) согласно требованиям, приведенным в таблице 6.
Дата добавления: 2016-03-10 ; просмотров: 5466 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник