2.3. Машинное представление информации
Информацию, представленную в виде, пригодном для её автоматизированной обработки, называют данными.
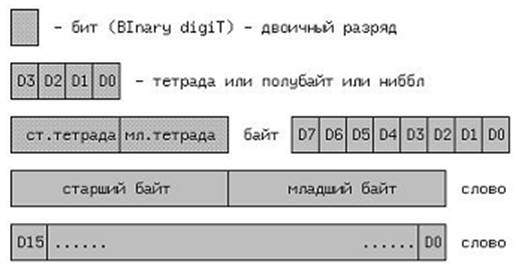
В цифровых устройствах данные представляются в двоично-кодированной форме. Основными структурными единицами данных являются: бит, поле, байт, слово.
Бит (сокращение от англ. binary digit – двоичная цифра) – это такое количество информации, которое может быть записано в одном разряде разрядной сетки, например 0 или 1.
Последовательность битов, имеющая определённый смысл, называется полем (поле кода операции, поле адреса и т. д.).
Поле, состоящее из 8 битов, называется байтом (от англ. byte – слог, часть). Байт в цифровой технике используется для представления и записи любого символа, а также является наименьшей адресуемой единицей для записи и хранения данных в запоминающих устройствах. На основе байтов строятся любые другие укрупнённые единицы данных (слово – 2 байта, двойное слово – 4 байта, учетверённое слово – 8 байт, килобайт – 2 10 10 3 байт, мегабайт – 2 20 10 6 байт, гигабайт – 2 30 10 9 байт, терабайт – 2 40 10 12 байт).
Словом называется последовательность, состоящая из строго определённого числа байтов, принятого для данного цифрового устройства.
— тетрада или полубайт или ниббл
2.3.1 Формы представления чисел.
На основе принятой структуры разнообразные данные организуются в соответствии со следующими форматами:
а) числовые данные с фиксированной точкой делятся на беззнаковые (например, адреса памяти) и обычные числа со знаком. Каждый тип данных может быть представлен в четырёх форматах: наименьшем (один байт), коротком (одно слово), среднем (двойное слово), длинном (учетверённое слово);
б) для числовых данных с плавающей точкой используется три формата: короткий (4 байта, из них мантисса со знаком – 3 байта, порядок со знаком – 1 байт), средний (8 байт, из них мантисса со знаком – 53 бит, порядок со знаком – 11 бит), длинный (10 байт, из них мантисса со знаком – 65 бит, порядок со знаком – 15 бит);
в) для представления двоично-десятичных данных (BCD) применяется два формата: упакованный и неупакованный;
В упакованном формате в каждом байте размещаются две десятичные цифры. Для знака отводится старшая тетрада дополнительного старшего байта (для положительных чисел – 1100, для отрицательных – 1101). Упакованный формат используется для выполнения арифметических операций.
В неупакованном формате десятичные цифры кодируются в соответствии с американским стандартным кодом обмена информацией ASCII. При этом в каждом байте (в младшей тетраде) размещается только одна десятичная цифра, а в старшей тетраде записывается 0011 (в соответствии с кодом ASCII). Для знака числа отводится старший байт (для положительных чисел – 2BH, для отрицательных – 2DH). Неупакованный формат используется для обмена двоично-десятичными данными между процессором и внешними устройствами;
г) для представления и отработки текстовой информации используются специальные информационные структуры переменного формата – строки. Строка представляет непрерывную последовательность битов, байтов, слов или двойных слов. Битовая строка может быть длиной до 1 Гбита, а длина остальных строк может достигать 4 Гбайт.
Существуют две основные формы представления чисел, которые используются для обработки в цифровых устройствах:
— числа с фиксированной запятой (точкой);
— числа с плавающей запятой (точкой).
Числа с фиксированной запятой могут быть целыми, если запятая зафиксирована справа от младшего разряда, или дробными, если слева от старшего разряда.
Числа с фиксированной запятой, как было показано ранее допускают достаточно простые способы выполнения арифметических операций, но имеют весьма ограниченный диапазон возможных значений, -(2 
-1)…0…(2 -1), поэтому используются лишь в простых приложениях.
В ЭВМ вещественные числа D хранятся и используются в показательной форме, т. е. в виде двух составляющих: мантиссы M и смещенного порядка E:
D=±M*2 
;
Смещение порядка необходимо для того, чтобы можно было представлять числа меньше единицы.
При этом числа обычно представляются в виде нормализованной мантиссы, имеющей 23 разряда, где первая значащая цифра «1» мысленно находится слева от запятой, а справа располагаются 23 разряда: 1,ххх…ххх. Поэтому М 
=1,111…111=1+1/2+1/4+1/8+…=2, а М 
=1,000…000=1. Разряд знака мантиссы равен 0 для положительного числа и равен 1 для отрицательных чисел. При этом разряд знака записывается слева от значащих цифр мантиссы и таким образом число мантиссы имеет 24 разряда. Порядок числа записывается 8-ми разрядным двоичным числом, при этом максимальный порядок составляет Е =11111110=254, а минимальный Е =00000001=1. Диапазон изменения чисел при этом составляет от +D =M *2 
=3,4*10 
до +D =M *2 
=1,17*10 
. Точность представления определяется числом разрядов мантиссы. При 23 двоичных разрядах 2 
10 
, т. е. достоверными являются только 6-7 значащих цифр, а не 38. Следует отметить, что значения порядка 11111111 и 00000000 по международному стандарту IEEE 754 и 854 предназначены для кодирования денормализованных чисел, отрицательной и положительной бесконечностей, неопределенностей и специальных чисел.
Источник
Машинное представление информации
Микропроцессоры обрабатывают упорядоченные двоичные наборы. Минимальной единицей информации является один бит.
Далее следуют — тетрада (4 бита), байт ( byte 8 бит), двойное слово (DoubleWord 16 бит) или длинное (LongWord 16 бит) и учетверенное слова. Младший бит обычно занимает крайнюю правую позицию.
4. Числа с фиксированной точкой
Такие числа могут быть как целыми, так и дробными. Точка мысленно фиксируется рядом с любым разрядом. Если она располагается справа от младшего бита, то число целое, если слева от старшего — число дробное. Далее будут рассматриваться только целые числа с фиксированной точкой, для нецелых чисел чаще применяется показательная форма, о которой пойдет речь дальше.
Естественным представлением целого неотрицательного числа является двоичная система счисления. Кодирование отрицательных чисел производится тремя наиболее употребительными способами, в каждом из которых крайний левый бит — знаковый. Отрицательному числу соответствует единичный бит, а положительному — нулевой. Каждый способ оценивается по скорости и затратам на выполнение сложения и изменения знака числа, т.к. вычитание есть сложение с измененным знаком одного операнда.
4.1 Прямой код
Изменение знака производится просто, путем инверсии бита знака. Пусть 00001001 = 9, тогда 10001001 = -9. Если при сложении двух чисел в этом коде знаки совпадают, то трудностей нет. Если знаки различаются необходимо найти наибольшее число, вычесть из него меньшее, а результату присвоить знак наибольшего слагаемого.
4.2 Обратный код, инверсный или дополнительный «до 1»
Изменение знака производится просто — инверсией всех бит: 00001001 = 9, а 11110110 = -9. Сложение также выполняется просто, т.к. знаковые биты можно складывать. При переносе единицы из левого (старшего) бита, она должна складываться с правым (младшим). Например: 7 + (-5) = 2.
11111010 =-5 (инверсия 00000101 = 5)
Сложение в обратном коде происходит быстрее, т.к. не требуется принятие решения, как в предыдущем случае. Однако суммирование бита переноса требует дополнительных действий. Другим недостатком этого кода является представление нуля двумя способами, т.к. инверсия 0. 00 равна 1. ..11 и сумма двух разных по знаку, но равных по значению чисел дает 1. 11.Например: (00001001 = 9) + (11110110 = -9) = 11111111. Кстати, из этого примера понятно почему код называется дополнительным «до 1».
4.3 Дополнительный или дополнительный «до 2» код
Число с противоположным знаком находится инверсией исходного и добавлением к результату единицы. Например, найти код числа -9.
00001001 = 9 11110111 =-9
11110110 — инверсия 00001000 — инверсия
11110111 =-9 00001001 = 9
Проблемы двух нулей нет. +0 = 00000000, -0 = 11111111 + 1 = 00000000 (перенос из старшего бита не учитывается).Сложение производится по обычным для неотрицательных чисел правилам.
Из этого примера видно, что в каждом разряде двух равных по модулю чисел складываются две единицы, что и определило название способа. Этот метод применяется наиболее часто, и когда говорят о дополнительном коде, то имеется в виду дополнительный «до 2-х» код.
5. Схема алгоритма
Программная реализация алгоритма
Общие сведения
Программа написана на языке Turbo Pascal 7.0 . Минимальные требования к конфигурации системы: процессор 80386 и выше. Исполняемый файл MS-DOS «v1_13.exe».
Файл с исходными данными должен находиться в том же каталоге, что и «v1-13.exe», и носить название «in.txt». Файл результатов работы — «out.txt».
Данные должны быть целыми числами(возможно со знаком) в диапазоне от –128..+127, т.к. для реализации задачи была выбрана 8 разрядная двоичная сетка.
Описание использованных функций и процедур
В данной работе для перевода из одной системы в другую используется несколько функций:
v DecToBase – выполняет перевод из десятичной в 2-16 системы счисления;
v BaseToInt – обратный перевод из Base-системы счисления в десятичную СС;
DecToBase
Данная функция является программным осуществлеием алгоритма преобразования числа из десятичной системы счисления в любую другую, описанного выше.
Удобство функции заключается в том, что она чувствительнак знаку числа и по умолчанию при переводе в двоичную систему счисления использует дополнительный «до 1» код, что избавляет нас от написания дополнительной функции перевода.
BaseToInt
Данная функция реализует алгоритм преобразования числа Base- системы счисления в десятичную по следующей формуле:
p-основание СС; Х – десятичное представление числа.
Функция определяет знак числа за счет учета инверсии: т.к. используем 8 разрядную двоичную сетку и числа со знаком, то имеет 128 отрицательных и 127 положительных значений и ноль (всего 256), то есть отрицательная величина лежит в диапазоне беззнаковых значений 128..256. А выражение (256- ), где — беззнаковая величина после преобразования, есть модуль отрицательного числа.
Источник
Машинное представление информации.
Машинное представление информации.
Числа с фиксированной точкой.
Вещественные числа с плавающей точкой .
Машинные двоичные коды.
Учебная литература: [1], [6], [7], [11].
Машинное представление информации
В ЭВМ обрабатываются упорядоченные двоичные наборы. Единицы измерения информации в ЭВМ приведены на рисунке 2.1. Минимальной единицей информации является один бит.
Рисунок 2.1 – Единицы измерения информации в ЭВМ
Далее следуют – тетрада (4 бита), байт (byte – это 8 бит), двойное слово (DoubleWord – 16 бит) или длинное (LongWord 16 – бит) и учетверенное слова. Младший бит обычно занимает крайнюю правую позицию.
Формы представления чисел
В ЭВМ применяются две формы представления чисел:
— с фиксированной запятой;
— плавающей запятой.
Данные, хранящиеся в ячейках памяти и регистрах ЦВМ в формате с фиксированной запятой, имеют постоянное число разрядов слева и справа от запятой. Сама запятая не реализуется техническими средствами, ее положение учитывается при составлении программ.
Чаще всего запятая условно фиксируется сразу после знакового разряда. В этом случае в ЦВМ используются только числа, абсолютная величина которых не больше единицы.
Прежде чем рассмотреть каждую из форм представления чисел запишем некоторое произвольное число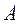 
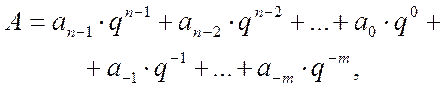
в виде полинома
(2.1)
где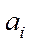 
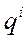
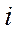
– цифра из алфавита цифр выбранной позиционной системы счисления (ПСС);
– основание ПСС;
– коэффициент, учитывающий позицию (место расположения) цифры в составе числа.
Затем преобразуем формулу (2.1) к виду:
(2.2)
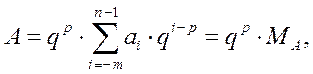
где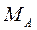 
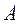
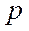
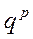
– цифровая часть числа , называемая его мантиссой;
– целое число, которое называют порядком, который определяет место точки в числе;
– множитель называемый масштабом.
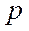
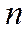
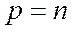
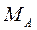
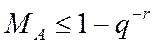
Для чисел c фиксированной запятой (ФЗ) величина постоянна и обычно равна 
. При 
мантисса числа будет правильной дробью, причем
(2.3)
где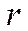 
– количество разрядов, используемых для записи мантиссы числа.
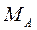
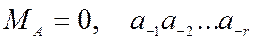
Изображается мантисса записью вида
. (2.4)
В ЭВМ с ФЗ любое число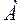 
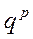
представляется только своей мантиссой, а масштаб в машине никак не отображается. Поэтому масштабы чисел необходимо учитывать в алгоритмах решаемых задач. Это делается путем масштабирования всех исходных данных и результатов всех операций в математическом списании задачи так, чтобы не допустить нарушения условия (2.3). В противном случае происходит грубое искажение результата из-за потери в ЭВМ старших разрядов мантиссы.
Достоинствами представления чисел в форме с ФЗ являются:
— малый расход оборудования для представления числовой информации;
— высокая производительность арифметико-логического устройства (АЛУ), обусловленные простотой алгоритмов выполнения арифметических операций.
Недостаток – необходимость осуществления масштабирования исходных данных на этапе подготовки вычислений.
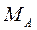
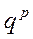
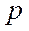
Для чисел c плавающей запятой (ПЗ) требуется отображение не только мантиссы каждого числа, но и его масштаба . Для представления последнего достаточно записать только его порядок .
Основное достоинство такого представления в том, что отпадает необходимость в масштабировании переменных.
Недостатками является:
— сложность алгоритмов реализации арифметических операций.
— увеличение объема оборудования, в связи с необходимостью выполнения действий и над мантиссами чисел и над их порядками;
— снижение производительности ЭВМ.
К бортовым ЦВМ (БЦВМ) предъявляются жесткие ограничения на массогабаритные характеристики и время выполнения арифметических операций.
Одним из путей достижения этих ограничений является использование представления чисел с фиксированной запятой. А сами числа должны быть представлены в виде правильных дробей, целая часть которых равна нулю. В связи с этим между числом и его представлением в ЦВМ существуют отличия.
Число, преобразованное для размещения внутри ЦВМ, называется машинным кодом.
Машинные двоичные коды
Двоично-десятичный код
Двоично-десятичный код (ДДК) или Binary Coded Decimal (BCD) может быть упакованным, когда в одном байте хранятся две десятичные цифры, либо неупакованным – по одной цифре в байте. Упакованное число 1996 представляется в виде двух байтов: 0001 1001 и 1001 0110. Для знака числа отводится дополнительный байт, например, в формате (ДД) девять байтов отводится для размещения 18-ти цифр, а в старшем бите десятого байта находится знак числа.
Буквенно-цифровой код
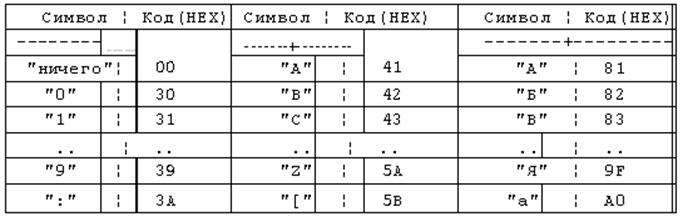
Для вывода информации на устройства отображения, например дисплей или принтер, а также для ввода или передачи данных используются буквенно-цифровые коды. Буквы, цифры, математические символы, знаки препинания, символы для рисования линий, управляющие символы и некоторые другие (таблица 2.1) кодируются однобайтовыми числами. Существует несколько разновидностей таких кодов, например: ASCII, КОИ-7, КОИ-8, альтернативный код ГОСТ, основной код ГОСТ и другие. ASCII и 7-ми битовый код для обмена информацией (КОИ-7) отображают первые 128 символов и входят в состав остальных кодировок. Дополнительные символы и русский алфавит входят в восьмибитовые расширенные коды (КОИ-8, альтернативный и основной). Общее число символов в этих кодах равно 256. Таблица некоторых кодов приведена ниже. Следует отметить, что нулевой код (NULL) не кодирует цифру ноль и вообще никак не отображается.
Таблица 2.1 – Примеры буквенно-цифровых кодов
В Internet для русского языка используется кодировка КОИ-8. В настоящее время разработан и используется 16-ти битовый Unicode с 65536 различными симвоволами.
Восьмисегментный код
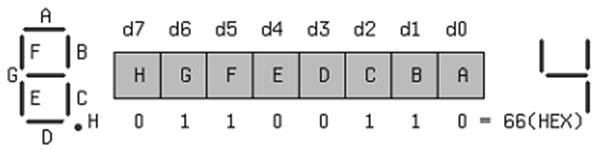
Служит для отображения образа BCD или HEX цифры высвечиваемой на индикаторе в виде набора 0 и 1. Может быть принято следующее соответствие между битами и сегментами (рисунок 2.6), где приведен битовый набор для высвечивания цифры 4. Единицы обычно соответствуют светящимся сегментам.
Рисунок 2.6 – Соответствие между битами кода и сегментами цифрового
Индикатора для цифры «4»
Машинное представление информации.
Источник
