Магический квадрат способы составления
МЕТОДЫ ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ
Уважаемые читатели! Эта страница является Приложением к главе “Магические квадраты” из книги “Компьютер решает головоломки”. Она адресована тем, кого заинтересовала тема “Магические квадраты”. Изложенные методы построения магических квадратов я нашла в литературе (в основном это журналы “Наука и жизнь”). Но! не нашла методов построения магических квадратов чётного (или: чётно-нечётного) порядка, не являющихся чётно-чётными (то есть порядок таких квадратов делится на число 2, но не делится на число 4), например, шестого, десятого и т. д. Этот метод я изобрела сама. Поэтому я пока не привожу его здесь. Делаю заявку на изобретение нового метода, которого нет в литературе! Я не могу сказать со 100% уверенностью, что в литературе вообще нет методов построения магических квадратов чётно-нечётного порядка. Надо поискать получше. Но даже если они и есть, то, вполне возможно, что они отличаются от метода, придуманного мной. Приглашаю всех заинтересовавшихся рассмотреть тему подробно и сообщить мне, нашлись ли такие методы. Или мой метод пока единственный?
А теперь перехожу к методам построения магических квадратов нечётного и чётно-чётного порядка.
Магические квадраты нечётного порядка
Если магический квадрат третьего порядка нетрудно построить простым перебором всевозможных комбинаций, то, уже начиная с квадрата четвёртого порядка, дело осложняется. Вы убедились в этом, если решали задачу о магическом квадрате четвёртого порядка, приведённую в разделе 1. Математики изобрели несколько методов построения магических квадратов. Начнём с метода террас, который применяется для построения магических квадратов нечётного порядка: пятого, седьмого и т. д. Рассмотрим его на примере магического квадрата пятого порядка.
С четырёх сторон к исходному квадрату 5х5 добавляются террасы так, чтобы получился зубчатый квадрат того же порядка, что и исходный (рис. 1). В полученной фигуре располагают числа от 1 до 25 в естественном порядке косыми рядами снизу вверх (рис. 1) или сверху вниз (рис. 2). Числа в террасах, не попавшие в квадрат, перемещаются как бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным сторонам квадрата. На рис. 3 и 4 изображены готовые магические квадраты, они аналогичны по структуре, только один повёрнут на 90 градусов относительно центра квадрата. Заметим, что методом террас можно построить не только традиционный магический квадрат нечётного порядка (то есть заполненный числами от 1 до n 2 ), но и квадрат, заполненный любыми другими числами, лишь бы разность между каждым последующим и предыдущим числом была постоянной. Так, на рис. 5 вы видите нетрадиционный магический квадрат пятого порядка, заполненный чётными числами от 2 до 50, построенный методом террас. Предлагаю вам построить методом террас магические квадраты седьмого и/или девятого порядка.
Источник
Магический квадрат способы составления
«Математика-это дверь и ключ к наукам».
Слово « математика» пришло к нам из древнегреческого, означает «учиться», «приобретать знания». И не прав тот, кто говорит: «Мне не нужна математика, я ведь не собираюсь стать математиком». Математика нужна всем! Математика учит нас учиться приобретать знания. А многообразие математических тем, которые можно рассмотреть, завораживает, поэтому выбор темы становится одним из этапов исследования, то есть приобретения новых знаний. Мой выбор пал на «Магические квадраты». Само понятие «магические квадраты» содержит тайну, загадку, а после знакомства с историей и некоторыми свойствами этих квадратов, возникает желание продолжать исследование.
Почему я выбрал такую тему? В наше время популярный вид досуга — решение судоку, головоломок с числами (в том числе и компьютерные головоломки), которые напрямую связаны со свойствами магических квадратов.
Изучение магических квадратов, их свойств может помочь в развитии:
интереса к предмету математики
А так же решение задач, связанных с магическими квадратами:
предотвращает заболевания, связанные с нарушением работы головного мозга.
Можно ли, используя методы математики, научиться быстро решать судоку, головоломки с числами?
изучение истории появления магических квадратов и способов их заполнения
познакомиться с магическими квадратами
узнать историю возникновения квадратов
изучить правила составления и заполнения магические квадраты
научиться правильно и быстро строить магические квадраты
рассмотреть разновидности магических квадратов
узнать, знакомы ли мои одноклассники с чудесными квадратами
предположить пути дальнейшего исследования
Для заполнения магических квадратов должны существовать специальные способы, которые позволяют сделать это быстро.
изучение специальной литературы;
поиск информации в сети Интернет;
анализ и обобщение.
Глава 1.Теоретическая часть:
1.1. Из истории возникновения магических квадратов.
Магический квадрат один из наиболее древних головоломок – древнекитайского происхождения . Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы . Эти знаки известны под названием ло-шу и равносильны магическому квадрату. Ло-шу (Приложение 1) использовали в магических обрядах при заклинаниях.
В 11 в. о магических квадратах узнали в Индии, а затем в Японии.
Из Индии сведения о магических квадратах перешли к арабам. Арабы были знакомы с квадратом третьего порядка в VIII веке, а в XII веке его описал в своих сочинениях Ибн Эзра. Мусульмане очень благоговейно относились к квадратам пятого порядка с цифрой 1 в середине, считая это изображение символом единства Аллаха.
Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос, живший в Константинополе .
Первым квадратом, придуманным европейцем, считается квадрат (Приложение 2)немецкого художника Альбрехта Дюрера (1471 – 1528), выпустивший в 1514 году гравюру «Меланхолия», на которой в правом верхнем углу есть изображение магического квадрата четвёртого порядка. Причём два числа в середине нижней строки указывают на год создания гравюры -1514. Этот факт говорит об умении в то время составлять магические квадраты с определённым расположением некоторых чисел. Говорят, что гравюра А. Дюрера послужила толчком для знаменитых пророчеств его современника Мишеля Нострадамуса (1503- 1566).
В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет — Сатурном, Юпитером, Марсом, Солнцем, Венерой, Меркурием, и Луной. (Приложение 3)
В Западной Европе в средние века магические квадраты были достоянием представителей алхимии и астрологии. Бытовало поверье, что выгравированный на серебре магический квадрат защищает от чумы.
От суеверных представителей древних китайцев, индусов, европейских алхимиков и астрологов эти числовые квадраты и получали своё необычное для математики название – «магические» квадраты. Иногда по отношению к ним употребляется слово «волшебные», но значительно реже, чем «магические». Даже сегодня среди атрибутов европейских прорицателей можно увидеть магические квадраты. А любителям математики составление квадратов служило хорошей гимнастикой ума и одно время столь же процветало, как увлечение кроссвордами в наши дни.
В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
1.2 . Разновидности магических квадратов.
Источник
Способы заполнения магических квадратов
2. Способы заполнения магических квадратов
Магические квадраты нечетного порядка
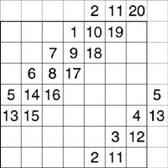
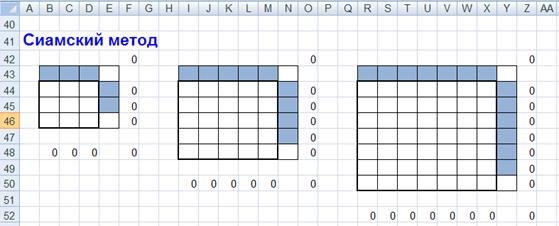
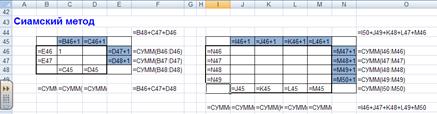
Магические квадраты нечетного порядка можно построить с помощью метода французского геометра 17 в. А.де ла Лубера (сиамский метод). Рассмотрим этот метод на примере квадрата 5-го порядка (рис. 4). Число 1 помещается в центральную клетку верхней строки. Все натуральные числа располагаются в естественном порядке циклически снизу вверх в клетках диагоналей справа налево. Дойдя до верхнего края квадрата, продолжаем заполнять диагональ, начинающуюся от нижней клетки следующего столбца (по ломаной диагонали). Дойдя до правого края квадрата, продолжаем заполнять диагональ, идущую от левой клетки строкой выше. Дойдя до заполненной клетки или угла, траектория спускается на одну клетку вниз, после чего процесс заполнения продолжается.
Для облегчения заполнения квадрата данным методом, а именно определения места заполнения следующей клетки, после края квадрата можно воспользоваться следующей схемой
Поставим 1 в среднюю клетку верхнего ряда и продолжим последовательность по диагонали вправо-вверх. Если очередное число на диагонали выходит за границы квадрата, мы его переставляем в соответствующее поле в квадрат (см. рис.5).
Изучая различные источники, мы обратили внимание на то, что можно заполнять квадраты и в другом направлении и не обязательно 1 стоит в данной позиции.
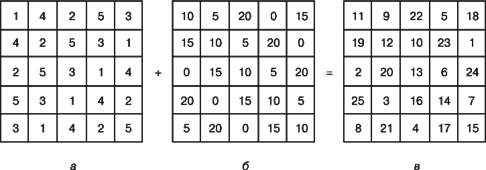
Метод Ф.де ла Ира (1640–1718) основан на двух первоначальных квадратах. На рис. 5 показано, как с помощью этого метода строится квадрат 5-го порядка. В клетку первого квадрата вписываются числа от 1 до 5 так, что число 3 повторяется в клетках главной диагонали, идущей вправо вверх, и ни одно число не встречается дважды в одной строке или в одном столбце. То же самое мы проделываем с числами 0, 5, 10, 15, 20 с той лишь разницей, что число 10 теперь повторяется в клетках главной диагонали, идущей сверху вниз (рис. 5,б). Поклеточная сумма этих двух квадратов (рис. 5,в) образует магический квадрат. Этот метод используется и при построении квадратов четного порядка.
Проанализировав данную схему заполнения по рисунку, мы пришли к следующему алгоритму.
1. В первом квадрате размещаем числа от 1 до n (порядок квадрата), так, чтобы на побочной диагонали стоял средний элемент этой последовательности.
2. Все остальные элементы располагаем параллельно этой диагонали по ломаным диагоналям. Элементы на ломаной диагонали равны. Числа в сроке и столбце не должны повторяться.
3. Во втором квадрате размещаем последовательные числа, кратные порядку квадрата, начиная с 0, (количество элементов равно порядку квадрата) так, чтобы на главной диагонали стоял средний элемент этой последовательности.
4. Все остальные элементы располагаем параллельно этой диагонали по ломаным диагоналям. Элементы на ломаной диагонали равны.
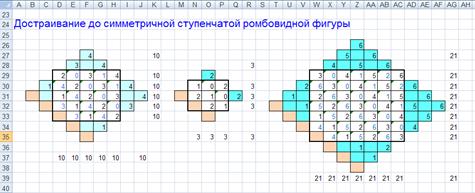
Достраивание до симметричной ступенчатой ромбовидной фигуры
Сначала исходный пустой квадрат достраивается до симметричной ступенчатой ромбовидной фигуры как показано на следующем рисунке.
 |
 |
| 24 | 20 | |||||
| 23 | 6 | 19 | 2 | 15 | ||
| 22 | 10 | 18 | 1 | 14 | 22 | 10 |
| 21 | 17 | 5 | 13 | 21 | 9 | 5 |
| 16 | 4 | 12 | 25 | 8 | 16 | 4 |
| 11 | 24 | 7 | 20 | 3 | ||
| 6 | 2 | |||||
| 1 |
Полученная на шаге 1 фигура заполняется по косым рядам снизу-вверх-направо целыми числами от 1 до n 2 последовательно. Результат заполнения показан на следующем рисунке:
| 25 | ||||
| 24 | 20 | |||
| 23 | 19 | 15 | ||
| 22 | 18 | 14 | 10 | |
| 21 | 17 | 13 | 9 | 5 |
| 16 | 12 | 8 | 4 | |
| 11 | 7 | 3 | ||
| 6 | 2 | |||
| 1 |
Каждое число, расположенное в фигуре вне исходного квадрата, переносится по вертикали или горизонтали внутрь исходного квадрата в самую удаленную клетку (на n клеток).
Способы заполнения магических квадратов порядка, кратного четырем
Универсальные методы составления магических квадратов произвольного четного порядка пока неизвестны. Однако, разработаны индивидуальные подходы для различных частных случаев. Ниже рассмотрен метод составления магических квадратов, порядок кратен 4. Этот метод удобно рассмотреть на примере магического квадрата 8-го порядка из натуральных чисел от 1 до 64. Метод включает следующую последовательность шагов.
1. Исходный квадрат делится на соответствующее число квадратов порядка 4. В данном случае таких квадратов будет 4. В каждом подквадрате закрашиваются диагональные элементы (главная и побочная).
2. Остальные элементы построчно заполняются порядковыми целыми числами в направлении слева -направо и сверху -вниз по закрашенным клеткам и справа -налево и снизу-вверх по не закрашенным клеткам.
3. Переход между цветами при заполнении происходит, если следующая для заполнения клетка меняет цвет
3. Реализация способов заполнения магических квадратов
с помощью программы Microsoft Excel.
Так как для составления магических квадратов необходимо всегда проверять контрольные суммы по строкам, столбцам и диагоналям, мы пришли к выводу, что этот процесс лучше автоматизировать. Для автоматизации мы выбрали программу Excel.
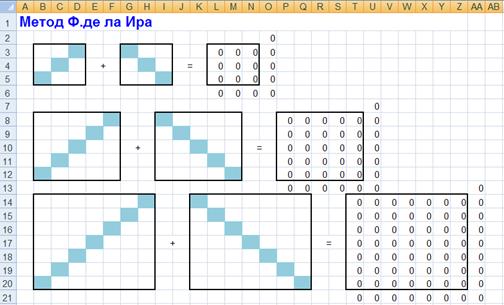
Используя функцию автосуммирования, мы подготовили шаблоны для вычисления контрольных сумм магических квадратов 3, 5 и 7 порядка по каждому из методов. А для метода Ф.де ла Ира еще и вычисление элементов третьего квадрата, как сумм соответствующих элементов первых двух квадратов.
В ходе экспериментальной части по методу Ф.де ла Ира , мы заметили, что в первых двух квадратах, элементы на ломаных диагоналях равны, и пришли в выводу, что процесс заполнения этих квадратов можно также автоматизировать. Достаточно указать только по одному элементу на каждой из ломаной диагонали.
Также для квадрата заданного порядка однозначны элементы на выделенных главных диагоналях, согласно алгоритму заполнения, поэтому их также можно занести в шаблон заполнения.
Внеся эти дополнения в шаблон, мы получили следующую заготовку для магических квадратов:
Теперь достаточно в первом квадрате на главной диагонали (в розовых клетках) разместить элементы с 1 до n. А во втором квадрате в первом столбце (так же в розовых клетках) элементы, кратные порядку квадрата.
В ходе экспериментальной части по способу достраивания до симметричной ступенчатой ромбовидной фигуры, мы заметили, процесс переноса чисел, вышедших за поле квадрата, также можно автоматизировать.
Элементы по диагонали каждый раз увеличиваются на единицу от предыдущего элемента, стоящего в этой диагонали. С учетом этого, достаточно вручную ввести только первые их элементы, а все остальные рассчитать по формулам.
Внеся эти дополнения в шаблон, мы получили следующую заготовку для магических квадратов данным способом:
Для построения магического квадрата, в клетки розового цвета внесем первых n чисел, которые при делении на порядок квадрата дают в остатке 1.
Для сиамского метода также можно автоматизировать заполнение и перенос чисел, вышедших за пределы квадрата.
4. Исследование количества решений магических квадратов.
Изучая литературу по теме, мы установили факт, что с увеличением размеров квадрата быстро растет количество возможных магических квадратов. Так, например, для 3 порядка – единственный, для 4 — 880, для 5 – приближается к четверти миллиона.
Изучив алгоритмы заполнения магических квадратов, нам захотелось экспериментировать: что произойдет, если мы поменяем местами элементы? Получится ли магическая сумма? Получим мы такой же квадрат или другой?
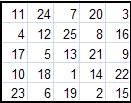
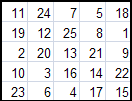
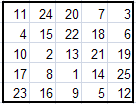
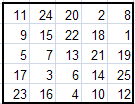
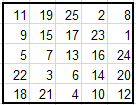
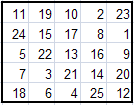
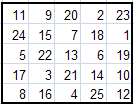
Вот некоторые магические квадраты, полученные методом Ф.де ла Ира.
Можно заметить, что все эти квадраты различны. Это только малая доля из всех возможных квадратов. С помощью программы Excel и подготовленных нами шаблонов, на их построение у нас уходит несколько секунд.
1. Магический квадрат – древнекитайского происхождения.
2. Универсального способа заполнения магических квадратов нет.
3. Способ заполнения магического квадрата, зависит от его порядка.
4. Для квадратов нечетного порядка существует 3 способа: метод Ф.де ла Ира (на двух квадратах), метод А.де ла Лубера (сиамский метод) и достраивание до симметричной ступенчатой ромбовидной фигуры.
5. Для квадратов, порядок которых кратен 4 существует способ разбиения на подквадраты порядка 4.
6. Известные методы для заполнения нечетных квадратов можно автоматизировать. Для этого идеально подходит программа Excel.
7. Эффективные шаблоны получаются для двух методов: Ф.де ла Ира и достраивания до симметричной ступенчатой ромбовидной фигуры.
8. С помощью подготовленных нами шаблонов можно создавать различные магические квадраты для одного и того же порядка.
В литературе есть ссылка, что метод, основанный на двух первоначальных квадратах, можно применить и для заполнения квадратов четного порядка. Экспериментируя, мы не пришли к нужному результату и оставляем это для дальнейшего исследования.
Использованные Интернет-ресурсы и литература:
4. И. Я. Депман, Н.Я. Виленкин. За страницами учебника математики. Москва. Просвещение. 1989г.
Источник