Магический квадрат способы построения

Основные методы построения магических квадратов с нечетным числом клеток

Статья просмотрена: 4973 раза

Библиографическое описание:

Бурханова, Ю. Н. Основные методы построения магических квадратов с нечетным числом клеток / Ю. Н. Бурханова, Е. А. Касаткина. — Текст : непосредственный // Молодой ученый. — 2010. — № 4 (15). — С. 29-35. — URL: https://moluch.ru/archive/15/1386/ (дата обращения: 19.11.2021).

Предлагаемая вниманию читателей статья посвящена вопросу, стоящему довольно далеко от центральной линии развития математической науки.

Священные, волшебные, загадочные, таинственные совершенные… Как только их не называли. Они пользовались особой популярностью у прорицателей, астрологов и врачевателей. Привлекающие своей красотой, наполненные внутренней гармонией, доступные, но по-прежнему непостижимые, скрывающие за кажущейся простотой множество тайн… Знакомьтесь: магические квадраты – удивительные представители воображаемого мира чисел.

Учение о магических квадратах занимало в математике значительное место лишь в тот период времени, когда всем руководили суеверия и астрология; в дальнейшем при возникновении новых естественнонаучных и технических задач теория магических квадратов стала не нужна. Однако учение о магических квадратах до сих пор может представлять интерес для любителей математики, в первую очередь для учащихся, в силу простоты и наглядности задач, не говоря уже о том, что это учение представляет собой благодарное поле приложения ряда более теоретико-числовых концепций.

Предлагаю вниманию читателя рассмотреть наиболее известные методы построения магических квадратов с нечетным числом клеток. При этом мы ограничиваемся лишь «классическими» магическими квадратами, т.е. квадратами, состоящими из последовательных натуральных чисел от 1 до .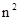

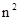
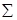
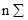
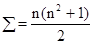
Числовым квадратом порядка n, где n – некоторое положительное целое число, мы будем называть квадрат, разбитый на n 2 клеток, в которых размещены ( в некотором порядке) целые числа от 1 до . Числовой квадрат мы будем называть магическим, если суммы, получаемые от сложения чисел каждого горизонтального ряда, каждого вертикального ряда и обеих диагоналей, одинаковы. Так как квадрат порядка n и сумма чисел каждого ряда одинакова, то сумма всех чисел, размещенных в магическом квадрате, равна . С другой стороны, она равна[3]

. (1)

Условия равенства суммы элементов отдельных строк, столбцов и диагоналей числу 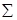мы будем называть условиями магичности этих строк, столбцов и диагоналей.[3]

Пример магического квадрата порядка 4 приведен на рис.1. (это так называемый квадрат Дюрера, изображенный на его гравюре «Меланхолия»). Для него в согласии с формулой (1), .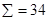

Рис.1. Квадрат Дюрера

Несмотря на то, что в свое время (особенно в XVI- XVIII веках) магические квадраты были предметом пристального изучения известных математиков, все же она не может считаться завершенной. Достаточно сказать, что до сих пор не известен никакой общий метод построения всех магических квадратов данного порядка n. Можно лишь утверждать, что это число делится на 8, так как из любого магического квадрата поворотами на 90 вокруг центра и отражениями в сторонах получаются еще 7 новых магических квадратов[4].

Клетки магического квадрата порядка n мы будем обозначать парами целых чисел (x,y) – их координатами, где х – номер вертикального ряда, у – номер горизонтального ряда, на их пересечении находится данная клетка[2]. При этом вертикальные мы нумеруем слева направо, а горизонтальные – снизу вверх. В качестве номеров мы будем использовать числа

Сдвигая основной квадрат параллельно самому себе на векторы с целочисленными координатами, делящимися на n, мы получим систему налегающих друг на друга квадратов порядка n, покрывающую всю плоскость. Две клетки, принадлежащим двум таким квадратам и занимающие относительно них одинаковое положение, мы будем называть эквивалентными. В дальнейшем эквивалентные клетки будут играть одинаковую роль и будут рассматриваться как одинаковые. Каждое целое число z=1, 2, . . ., n 2 мы можем записать в виде

где r и s – некоторые числа системы (2), однозначно определенные числом z и, обратно определяющее это число. Мы будем числа r и z называть координатами числа z[2].

Например, при n=3 координаты чисел

z=1, 2, 3, 4, 5, 6, 7, 8, 9

имеют соответственно вид

При задании некоторого магического квадрата порядка n каждой паре r,s сопоставляется пара чисел х, у – координаты клетки квадрата, в которую вписано число с координатами r, s. Другими словами, числа х и у являются функциями чисел r и s. Обозначая эти функции буквами f и g, мы получим, следовательно, что х = f(r, s) и у = g(r, s).

В дальнейшем любую пару f(r, s) и g(r, s) мы будем называть методом построения магических квадратов[2].

Описанное сведение задачи построения магического квадрата к задаче построения пары функций f(r, s) и g(r, s) позволяет, в частности, классифицировать способы построения магических квадратов в зависимости от характера этих функций.

Индийский метод составления магических квадратов (иногда называемые также сиамским) является, по-видимому, самым древним алгоритмом построения магических квадратов произвольного нечетного порядка n=2m+1. этот алгоритм описывают следующими правилами[2]:

1 . Числа от 1 до n2 поочередно вписываются в клетки основного квадрата.

2 . Если некоторое правило требует вписать данное число в клетку, лежащую вне основного квадрата, то вместо этого рассматриваемое число вписывается в эквивалентную клетку основного квадрата.

3 . Число 1 вписывается в среднюю клетку верхнего ряда, т.е. в клетку с координатами (m, 2m).

4 . Если число z вписано в клетку с координатами (х, у), то следующее число z+1 вписывается в клетку с координатами (х+1, у+1), т.е. в клетку, смежную с клеткой (х, у), в направлении восходящей диагонали, при условии, что эта последняя клетка еще свободна от чисел.

5 . Если клетка с координатами (х+1, у+1) уже занята некоторым числом, то число z+1 вписывается в клетку с координатами (х, у-1), т.е. в клетку, непосредственно примыкающую снизу к клетке (х, у). (оказывается это всегда возможно, т.е. клетка (х, у-1) обязательно свободна от чисел).

На рис.2 изображен магический квадрат третьего порядка, построенный индийским методом. Для ясности в этом рисунке заполнены также некоторые клетки вне основного квадрата. Не описывая подробно это построение, мы укажем лишь, что число 1 вписано на основании правила 1 и 3 , число 2 – на основании правил 4 и 2 , число 3 – на основании правил 4 и 2 , число 4 – на основании правил 5 и 2 , число 5 – на основании правила 4 , число 6 – на основании правила 4 , число 7 – на основании правил 5 и 2 , число 8 – на основании правил 4 и 2 и, наконец, число 9 – на основании правил 4 и 2 .

Источник

Магический квадрат способы построения

МЕТОДЫ ПОСТРОЕНИЯ МАГИЧЕСКИХ КВАДРАТОВ

Уважаемые читатели! Эта страница является Приложением к главе “Магические квадраты” из книги “Компьютер решает головоломки”. Она адресована тем, кого заинтересовала тема “Магические квадраты”. Изложенные методы построения магических квадратов я нашла в литературе (в основном это журналы “Наука и жизнь”). Но! не нашла методов построения магических квадратов чётного (или: чётно-нечётного) порядка, не являющихся чётно-чётными (то есть порядок таких квадратов делится на число 2, но не делится на число 4), например, шестого, десятого и т. д. Этот метод я изобрела сама. Поэтому я пока не привожу его здесь. Делаю заявку на изобретение нового метода, которого нет в литературе! Я не могу сказать со 100% уверенностью, что в литературе вообще нет методов построения магических квадратов чётно-нечётного порядка. Надо поискать получше. Но даже если они и есть, то, вполне возможно, что они отличаются от метода, придуманного мной. Приглашаю всех заинтересовавшихся рассмотреть тему подробно и сообщить мне, нашлись ли такие методы. Или мой метод пока единственный?

А теперь перехожу к методам построения магических квадратов нечётного и чётно-чётного порядка.

Магические квадраты нечётного порядка

Если магический квадрат третьего порядка нетрудно построить простым перебором всевозможных комбинаций, то, уже начиная с квадрата четвёртого порядка, дело осложняется. Вы убедились в этом, если решали задачу о магическом квадрате четвёртого порядка, приведённую в разделе 1. Математики изобрели несколько методов построения магических квадратов. Начнём с метода террас, который применяется для построения магических квадратов нечётного порядка: пятого, седьмого и т. д. Рассмотрим его на примере магического квадрата пятого порядка.

С четырёх сторон к исходному квадрату 5х5 добавляются террасы так, чтобы получился зубчатый квадрат того же порядка, что и исходный (рис. 1). В полученной фигуре располагают числа от 1 до 25 в естественном порядке косыми рядами снизу вверх (рис. 1) или сверху вниз (рис. 2). Числа в террасах, не попавшие в квадрат, перемещаются как бы вместе с террасами внутрь него так, чтобы они примкнули к противоположным сторонам квадрата. На рис. 3 и 4 изображены готовые магические квадраты, они аналогичны по структуре, только один повёрнут на 90 градусов относительно центра квадрата. Заметим, что методом террас можно построить не только традиционный магический квадрат нечётного порядка (то есть заполненный числами от 1 до n 2 ), но и квадрат, заполненный любыми другими числами, лишь бы разность между каждым последующим и предыдущим числом была постоянной. Так, на рис. 5 вы видите нетрадиционный магический квадрат пятого порядка, заполненный чётными числами от 2 до 50, построенный методом террас. Предлагаю вам построить методом террас магические квадраты седьмого и/или девятого порядка.

Источник

Магический квадрат — виды, правила и примеры решения

Среди поклонников логических игр большой популярностью пользуется магический квадрат. Он представляет собой таблицу, заполненную особым образом цифрами. Причём сумма чисел одинакова по всем направлениям. Эту величину принято называть константой. Существует множество вариантов таких головоломок разной степени сложности.

История и современное применение

Первые подобные таблицы использовались ещё в Древней Греции и Китае. Это подтверждено археологическими находками. Арабы называли квадраты магическими, так как верили, что они обладают волшебными свойствами и могут защитить от многих напастей.

В середине XVI в. вопросом о том, как работает магический квадрат, заинтересовались математики в Европе. Они начали активно исследовать загадочные сочетания цифр. Учёные стремились вывести общие принципы построения квадратов и найти всё множество возможных вариантов.

В современной общеобразовательной школе разные виды магических квадратов используются на уроках математики. Они способствуют развитию логического мышления и вызывают у детей живой интерес.

С их помощью школьники учатся планировать свою работу и контролировать её. В клетки можно вписывать не только отдельные цифры, но и математические выражения. Задачи на эту тему часто предлагаются на математических олимпиадах. Решать такие числовые задачи можно и онлайн.

Квадрат нечётного порядка

Среди несложных магических квадратов по математике выделяют разновидности чётного и нечётного порядка. Первая группа подразделяется на таблицы одинарной и двойной чётности.

Начальным шагом во всех случаях будет определение магической константы. Делается это с помощью специальной формулы [n * (n2 + 1)] / 2. Разобраться с принципом решения задачи этого класса можно на самом простом примере. Для этого выстраивается таблица из 9 ячеек. В неё нужно расставить цифры от 1 до 9. Дальнейший алгоритм:

Подсчитывается сумма, которая должна получиться в каждой строке. Для этого используется формула: 3 * (32 +1) / 2 = 3 * 10 / 2. Ответом будет число 15.

Числа в ячейках расставляются так, чтобы сумма их была равна 15 в каждой строчке. Это требует смекалки и воображения.

В средней клетке верхней строки вписывается 1.

Каждое следующее число ставится справа по диагонали вверх. Поставить цифру 2 нельзя, так как выше нет строк. Если мысленно добавить сверху ещё один квадрат, цифра 2 окажется в его нижнем правом углу. Значит, цифра 2 вписывается в нижнюю правую клетку.

По тому же принципу вписывается цифра 3. Она попадает в среднюю ячейку слева.

Если нужная клетка уже занята, очередной символ вписывается ниже предыдущего. Таким образом, 4 ставится под 3.

Записывается цифра 5 по диагонали вправо и вверх, а 6 в верхний угол справа.

Поскольку место цифры 7 уже занято, она вписывается ниже 6.

Восьмёрка занимает место в левом нижнем углу.

Оставшуюся клетку занимает девятка.

Общий алгоритм выполнения задания: каждый следующий знак пишется вверх и правее. Если там нет клетки — дорисовывается ещё один воображаемый квадрат. Если ячейка занята — число записывается ниже предыдущего. Таким способом можно составить любой квадрат нечётного порядка, включая самые сложные, с больши́м числом ячеек.

Одинарная чётность

Магические квадраты могут иметь порядок одинарной или двойной чётности. Для каждого случая предусмотрена отдельная методика вычисления. У таблиц одинарной чётности количество клеток в одной строке или столбце делится пополам, но не делится на четыре. Наименьшим квадратом, отвечающим этому требованию, будет прямоугольник 6х6. Фигуру 2х2 построить и заполнить невозможно.

Вычисление магической константы

Первый этап расчётов проводится по формуле [n * (n2 + 1)] / 2, где символом n обозначено число клеток в одном ряду. Если взять за пример квадрат 6х6, расчёт будет выглядеть следующим образом: [6 х (36 + 1)]: 2 = (6 х 37): 2 = 222:2.

Читайте также:  Деятельность как способ существования людей план для развернутого ответа

Волшебная постоянная прямоугольника со стороной 6 клеток равна 111. Общая сумма чисел от 1 до 36 в каждой строке и в разных направлениях должна быть равна 111.

Рисунок делится на 4 одинаковые части. В каждой будет по 9 клеток (3х3). Каждую часть обозначают латинскими буквами: А — верхняя левая, С — верхняя правая, D — нижняя левая и В — нижняя правая часть. Если квадрат имеет другой размер, n делится на 2, чтобы узнать точную величину каждой из 4 частей.

Дальнейшие действия

Следующий шаг — вписывание в каждую часть ¼ всех чисел. В квадрант А вносятся числа от 1 до 9, в квадрант В — от 10 до 18, в части С — от 19 до 27, в D — от 28 до 36.

Последовательность вписывания такая же, как при заполнении простейшего нечётного квадрата:

Минимальное число, которым начинается заполнение ячеек, всегда ставится в верхнем ряду посередине. У каждой части эта ячейка находится отдельно.

Каждая часть заполняется как новый математический объект. Даже если есть пустое место в другом квадрате, его в этих случаях игнорируют.

В блоках А и D на этой стадии решения сумма в строках и столбиках будет отличаться от постоянной. Чтобы это исправить, некоторые числа меняют местами между собой.

Алгоритм действий:

Начинать нужно с крайней левой клетки в верхней строке. Если фигура имеет размеры 6х6, выделяется только первая верхняя строка части А. В ней должно быть вписано число 8. Если величина таблицы составляет 10х10, выделяют 2 первые клетки в верхнем ряду. В них стоят 17 и 24.

Из выделенных клеток формируется промежуточный квадрат. В таблице с количеством строк и столбцов 6х6 он будет состоять из 1 клетки. Его условно обозначают А1.

Если размер 10х10, в верхней строке выделяется 2 первые ячейки. Вместе с ними выделяется ещё 2 клетки, во второй строке получается поле из 4 прилежащих друг к другу ячеек.

В следующей строке первая ячейка пропускается, затем выделяется столько клеток, сколько было в промежуточной таблице А1. Полученную фигуру можно обозначить А2.

Таким же способом строят промежуточный квадрат А3.

Эти 3 промежуточных фигуры формируют выделенную область А.

Далее переходят в квадрант D и формируют обособленную область D.

Цифры, которые были вписаны в выделенных треугольниках А и D, нужно поменять между собой местами. После этого сумма в каждой строке должна быть одинаковой. Она равняется вычисленной магической константе.

Двойной порядок

Если головоломка имеет порядок двойной чётности, количество окон в каждой горизонтальной строчке или вертикальном столбце должно делиться на 4. Минимальной фигурой с такими свойствами будет таблица 4х4.

Решать магические квадраты двойной чётности следует по тому же алгоритму, что и остальные. Первый шаг при заполнении — вычисление магической константы. Формула применяется та же, что для расчёта других квадратов. Для фигуры со стороной 4 клетки значение константы будет равно 34.

В каждом углу основного поля выделяются промежуточные таблицы. Их размер должен быть равен n/4. Эти области обозначают буквами A, B, C, D, располагая их против хода часовой стрелки. Величина промежуточных фигур зависит от размера исходного квадрата:

Если длина стороны составляет 4 ячейки, промежуточные зоны будут иметь по 1 клетке.

В таблице 8х8 эти области включают 4 элемента (2х2).

В квадрате 12х12 выделяются промежуточные фигуры размером 3х3.

Следующий этап — создание центрального промежуточного квадрата. Величина его стороны должна составлять n/2. Эта фигура не должна накладываться на периферические, но при этом соприкасаться с ними углами.

Далее в квадрат вносят цифры слева направо. Их допускается ставить только в свободные ячейки, которые входят в состав промежуточных областей. Например, при заполнении таблицы 4х4 порядок действий будет таким:

В первой сверху строке и первом слева столбце пишется 1. В верхней клетке четвертого столбика — 4.

В центр второй горизонтальной строчки ставятся цифры 6 и 7.

В четвёртой строке слева пишется 13, а справа — 16.

По этому же принципу цифрами заполняются оставшиеся клетки. Числа проставляются слева в порядке уменьшения. Если всё сделано верно, сумма всех чисел в любой строчке будет одинаковой.

Источник