Способы графического изображения показателей динамики
И структуры
Во многих случаях имеется необходимость на одной и той же координатной диаграмме отразить не одну, а несколько линий, характеризующих динамику различных абсолютных или относительных показателей либо однородного, либо неоднородного характера.
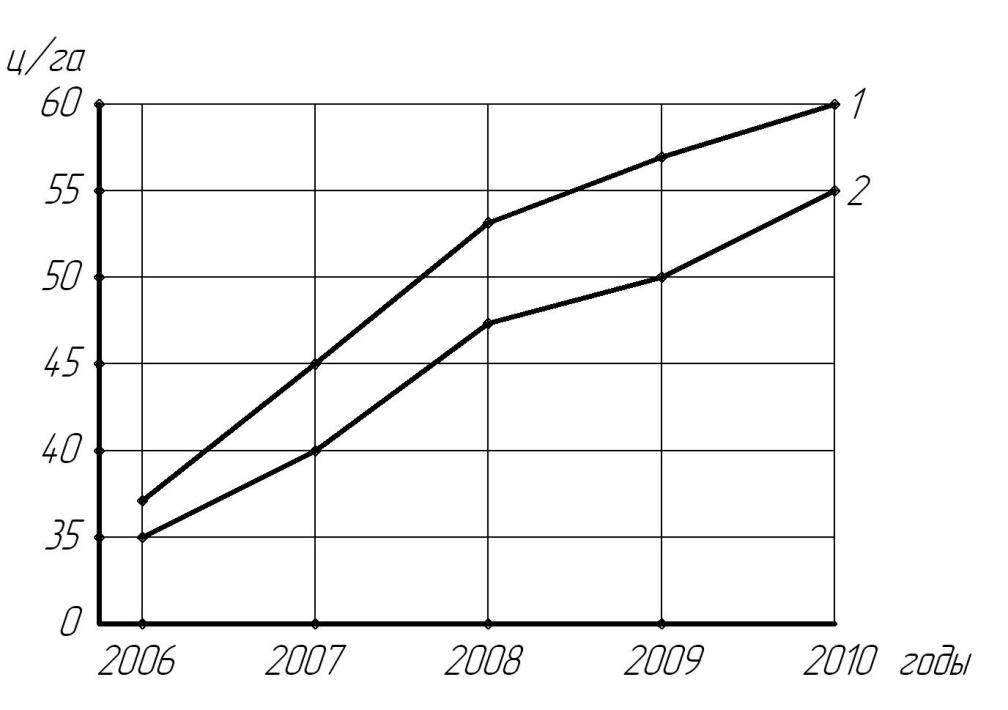
Если изображаемые на диаграмме показатели имеют однородныйхарактер (например, динамика урожайности отдельных видов зерновых культур), то их отражают в исходных единицах измерения. При этом каждую линию, характеризующую динамику отдельного вида культур, целесообразно расшифровать. Для этого достаточно обозначить наименование показателя с правой стороны диаграммы, против соответствующей линии. Примером такого способа графического изображения является комбинированная линейная диаграмма динамики урожайности озимых и яровых культур в сельскохозяйственной организации (рис. 5.2).
Рис. 5.2. Динамика урожайности озимых и яровых культур (линейная диаграмма):
1 – озимые; 2 – яровые
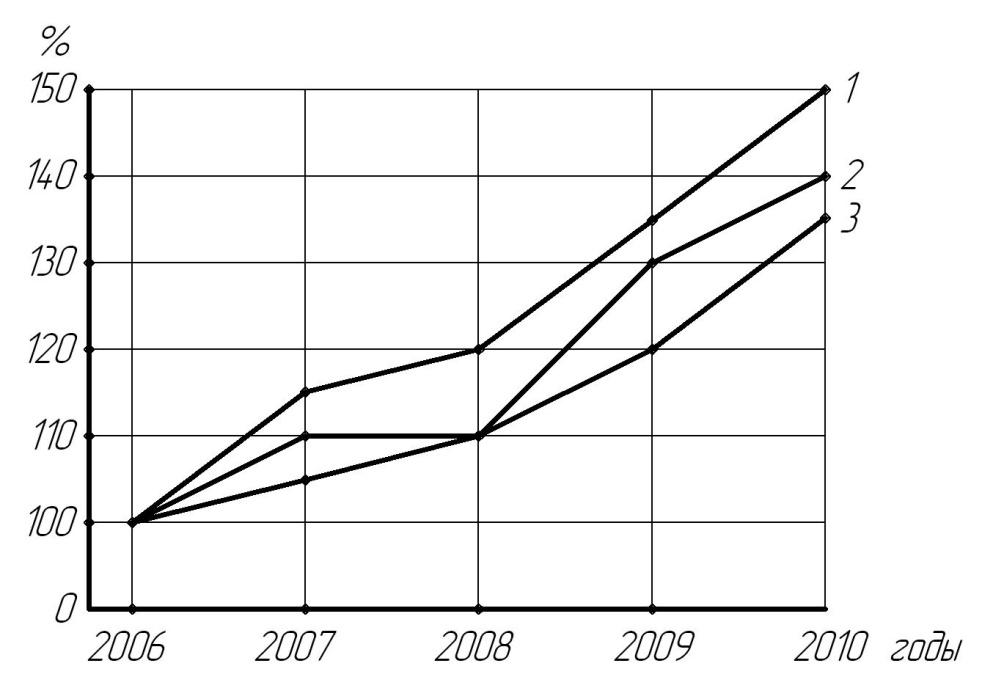
Нередки случаи, когда необходимо графически изобразить динамику нескольких неоднородных показателей на одной и той же линейной диаграмме. При этом целесообразно прежде всего абсолютные показатели динамики превратить в относительные величины, например, рассчитать базисные коэффициенты роста по каждому абсолютному показателю. Затем их размещают в системе координат, что позволяет наглядно проследить развитие динамики не только по каждому показателю в отдельности, но и сравнить динамику всех изображаемых неоднородных показателей (рис. 5.3).
Рис. 5.3. Динамика экспорта молочной продукции на молочном комбинате (линейная диаграмма): 1 – масло; 2 – сыры; 3 – казеин
При графическом изображении структуры сложных признаков могут быть применены секторные, квадратно-сетчатые, слоистые и др. виды диаграмм.
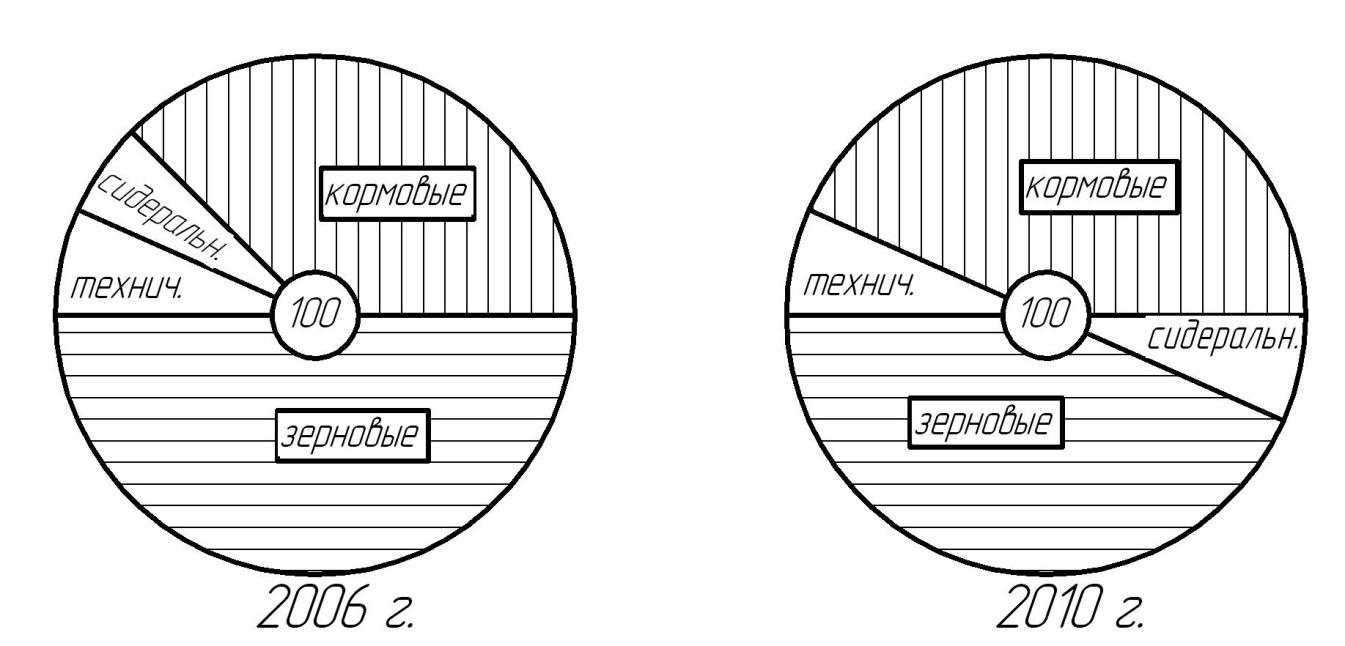
Секторная диаграмма– довольно распространенная форма наглядного сопоставления различных частей единого целого при помощи площадей, образуемых секторами круга. Она строится путем разделения круга на секторы пропорционального удельному весу частей в составе сложного признака. Размер каждого сектора определяется величиной угла из расчёта, что 1 % соответствует 3,6°. Во всех секторных диаграммах, независимо от величины круга, масштаб графика всегда постоянен, т.е. М: 1 % = 3,6°. Чтобы легче различать секторы, целесообразно пользоваться приёмом различной штриховки или цветной раскраски для каждого сектора (рис. 5.4).
Рис. 5.4. Структура посевных площадей в сельскохозяйственной организации «Днепр» (секторная диаграмма)
Секторные диаграммы обычно используются в тех случаях, когда необходимо графически изобразить структуру сложного показателя, например, за сравнительно небольшое число (2–3) промежутков или моментов времени, а также по небольшому числу однородных единиц или объектов.
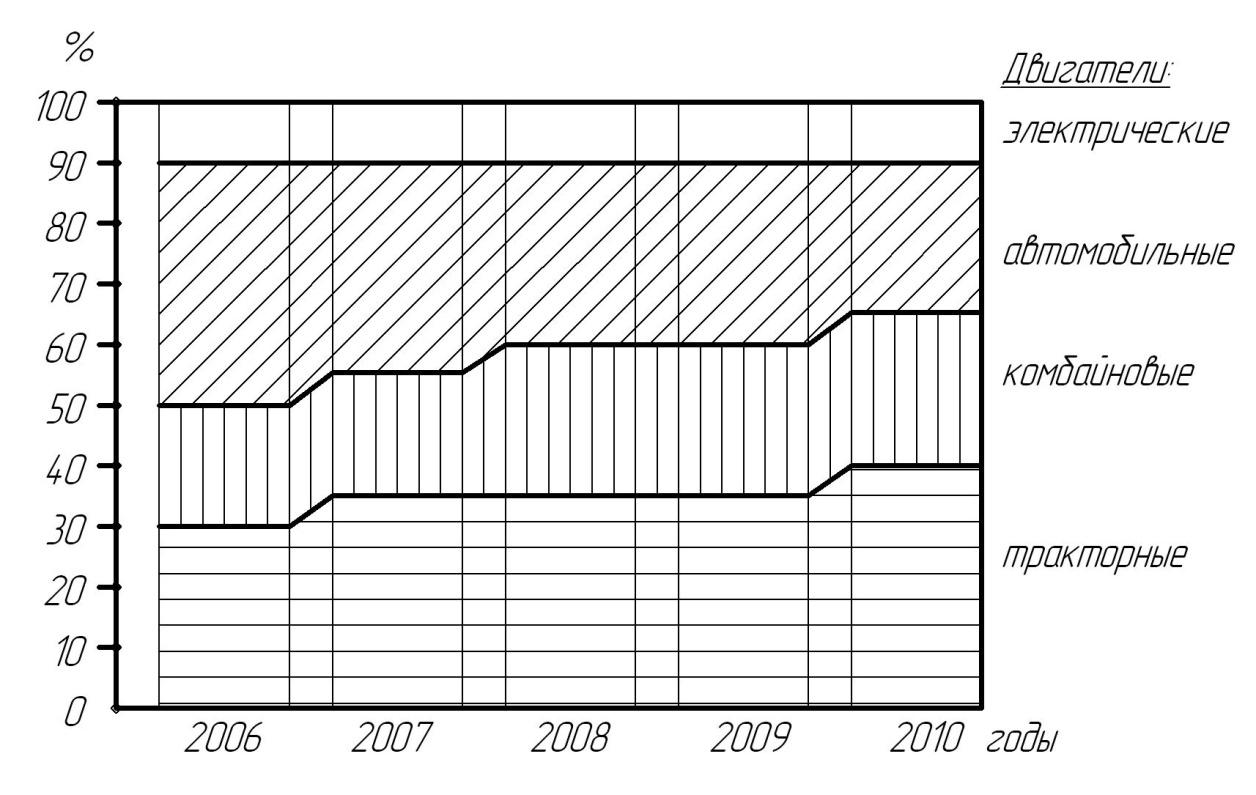
Если же структурные показатели требуется изобразить в длительной динамике (например, за 5 -–10 периодов), то в этом случае предпочтительнее воспользоваться способом слоистых диаграмм.Сущность его заключается в том, что на прямой горизонтальной линии размещают равные по основанию и высоте и одинаково отстоящие друг от друга столбики. Принимается условие, что каждый столбик – это общий (итоговый) структурный показатель за отдельный промежуток времени (например, за декаду, месяц, квартал, год и т.д.). Столбики по высоте делят на 100 равных частей, где каждая часть соответствует I %, Следовательно, на диаграмме высота каждой составной части пропорциональна ее удельному весу в составе всего сложного признака. Затем идентичные линии по каждой составной части во всех столбиках с помощью лекала соединяют, в результате чего за весь изучаемый период получаются слои, наглядно показывающие динамику удельных весов в составе сложного признака. Пример слоистой диаграммы представлен на рис. 5.5.
Рис. 5.5. Структура энергетических мощностей в сельскохозяйственной организации «Днепр» (слоистая диаграмма)
Квадратно-сетчатые диаграммы – это равные квадраты, разделенные на 100 одинаковых частей (квадратиков), полученных путем пересекающихся перпендикулярных линий. Это означает, что каждый квадратик равен 1/100 всей площади квадрата, т.е. I % объема сложного признака. Зная удельный вес каждой его составной части, нетрудно определить, сколько квадратиков может она занимать.
Квадратно-сетчатые диаграммы аналогично секторным могут быть использованы при графическом изображении структуры сложных признаков за сравнительно небольшое число периодов иди моментов времени, а также по небольшому количеству статистических единиц или объектов (рис. 5.6).
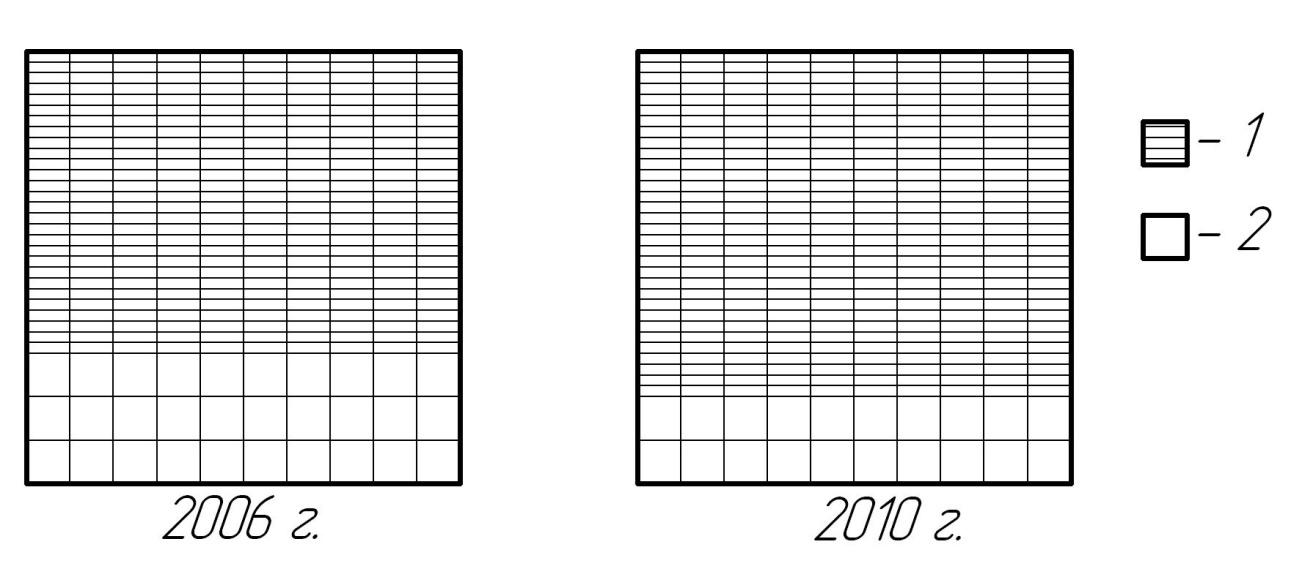
Рис. 5.6. Структура землепользования в сельскохозяйственной организации «Днепр» (квадратно-сетчатая диаграмма): 1 – с.-х. земли; 2 – не с.-х. земли
Источник
Графические методы представления статистических данных
Значение графического метода в анализе и обобщении данных велико. Графическое изображение, прежде всего, позволяет осуществить контроль достоверности статистических показателей, так как, представленные на графике, они более ярко показывают имеющиеся неточности, связанные либо с наличием ошибок наблюдения, либо с сущностью изучаемого явления. С помощью графического изображения возможны изучение закономерностей развития явления, установление существующих взаимосвязей. Простое сопоставление данных не всегда дает возможность уловить наличие причинных зависимостей, в то же время их графическое изображение способствует выявлению причинных связей, в особенности в случае установления первоначальных гипотез, подлежащих затем дальнейшей разработке.
Статистический график – это чертеж, на котором статистические совокупности, характеризуемые определенными показателями, описываются с помощью условных геометрических образов или знаков. Графический образ – это совокупность точек, линий и фигур, с помощью которых изображаются статистические данные. Вспомогательными элементами графика являются:
Поле графика – это часть плоскости, где расположены графические образы. Поле графика имеет определенные размеры, которые зависят от его назначения.
Пространственные ориентиры графика задаются в виде системы координатных сеток. Система координат необходима для размещения геометрических знаков в поле графика. Используются как прямоугольные, так и полярные системы координат.
Масштабные ориентиры используются для сопоставления графического отображения объекта и его реальных размеров. Задаются масштабные ориентиры системой масштабных шкал или масштабными знаками.
Экспликация графика состоит из объяснения предмета, изображаемого графиком (название), и смыслового значения каждого знака, применяемого на графике.
Статистические графики классифицируют по назначению (содержанию), способу построения и характеру графического образа (рис.1).
Рис.1. Классификация статистических графиков
По способу построения графических образов выделяют:
Диаграммы – графическое изображение статистических данных, наглядно показывающее соотношение между сравниваемыми величинами.
Различают следующие основные виды диаграмм: линейные, столбиковые, полосовые, секторные, квадратные, круговые, фигурные.
Линейные диаграммы применяются для характеристики динамики, т.е. оценки изменения явлений во времени. По оси абсцисс откладываются периоды времени или даты, а по оси ординат – уровни ряда динамики. На одном графике может быть размещено несколько диаграмм, что позволяет сравнивать динамику различных показателей, либо одного показателя по разным регионам или странам.
Рис.2. Динамика объема импорта легковых автомобилей в РФ
за 2006-1кв. 2010г.г.
Столбиковые диаграммы могут быть использованы:
для анализа динамики социально-экономических явлений;
оценки выполнения плана;
характеристики вариации в рядах распределений;
для пространственных сопоставлений (сравнения по территориям, странам, фирмам);
для изучения структуры явлений.
Столбики располагаются вплотную или раздельно на одинаковом расстоянии. Высота столбиков должна быть пропорциональна числовым значениям уровней признака.
Рис.3. Динамика удельного веса Белоруссии в товарообороте РФ со странами СНГ
Для характеристики структуры социально-экономических явлений широко используются секторные диаграммы. Для ее построения круг следует разделить на секторы пропорционально удельному весу частей в общем объеме. Сумма удельных весов равна 100%, что соответствует общему объему изучаемого явления.
Рис.4. Географическое распределение товарооборота РФ со странами СНГ
Полосовые диаграммы состоят из прямоугольников, расположенных горизонтально (полосами).
Иногда для сравнительного анализа по регионам, странам используют диаграммы фигур-знаков (диаграммы геометрических фигур). Данные диаграммы отражают размер изучаемого объекта в соответствии с размером своей площади.
Статистические карты применяются для оценки географического размещения явлений и сравнительного анализа по территориям.
Статистические карты включают картограммы и картодиаграммы. Различие между ними состоит в способах отображения статистических данных на картах.
Картограмма показывает территориальное распределение изучаемого признака по отдельным районам и используется для выявления закономерностей этого распределения. Картограммы делятся на фоновые и точечные. Фоновые картограммы разной густотой цветовой окраски характеризуют интенсивность какого-либо показателя в пределах территориальной единицы. На точечной картограмме уровень выбранного явления изображается с помощью точек.
Картодиаграмма – это сочетание географической карты или ее схемы с диаграммой. Она позволяет отразить специфику каждого района в распределении изучаемого явления, его структурные особенности.
В настоящее время разработаны различные пакеты прикладных программ компьютерной графики, например, Excel, Statgraf, Statistica.
Источник
5.4. Способы графического изображения показателей динамики и структуры
Во многих случаях имеется необходимость на одной и той же координатной диаграмме отразить не одну, а несколько линий, характеризующих динамику различных абсолютных или относительных показателей либо однородного, либо неоднородного характера.
Если изображаемые на диаграмме показатели имеют однородный характер (например, динамика урожайности отдельных видов зерновых культур), то их отражают в исходных единицах измерения. При этом каждую линию, характеризующую динамику отдельного вида культур, целесообразно расшифровать. Для этого достаточно обозначить наименование показателя с правой стороны диаграммы, против соответствующей линии. Примером такого способа графического изображения является комбинированная линейная диаграмма динамики урожайности озимых и яровых культур в сельскохозяйственной организации (рис. 5.2).
Рис. 5.2. Динамика урожайности озимых и яровых культур (линейная диаграмма):
1 – озимые; 2 – яровые
Нередки случаи, когда необходимо графически изобразить динамику нескольких неоднородных показателей на одной и той же линейной диаграмме. При этом целесообразно прежде всего абсолютные показатели динамики превратить в относительные величины, например, рассчитать базисные коэффициенты роста по каждому абсолютному показателю. Затем их размещают в системе координат, что позволяет наглядно проследить развитие динамики не только по каждому показателю в отдельности, но и сравнить динамику всех изображаемых неоднородных показателей (рис. 5.3).
Рис. 5.3. Динамика экспорта молочной продукции на молочном комбинате (линейная диаграмма): 1 – масло; 2 – сыры; 3 – казеин
При графическом изображении структуры сложных признаков могут быть применены секторные, квадратно-сетчатые, слоистые и др. виды диаграмм.
Секторная диаграмма – довольно распространенная форма наглядного сопоставления различных частей единого целого при помощи площадей, образуемых секторами круга. Она строится путем разделения круга на секторы пропорционального удельному весу частей в составе сложного признака. Размер каждого сектора определяется величиной угла из расчёта, что 1 % соответствует 3,6. Во всех секторных диаграммах, независимо от величины круга, масштаб графика всегда постоянен, т.е. М: 1 % = 3,6. Чтобы легче различать секторы, целесообразно пользоваться приёмом различной штриховки или цветной раскраски для каждого сектора (рис. 5.4).
Рис. 5.4. Структура посевных площадей в сельскохозяйственной организации «Днепр» (секторная диаграмма)
Секторные диаграммы обычно используются в тех случаях, когда необходимо графически изобразить структуру сложного показателя, например, за сравнительно небольшое число (2–3) промежутков или моментов времени, а также по небольшому числу однородных единиц или объектов.
Если же структурные показатели требуется изобразить в длительной динамике (например, за 5 -–10 периодов), то в этом случае предпочтительнее воспользоваться способом слоистых диаграмм. Сущность его заключается в том, что на прямой горизонтальной линии размещают равные по основанию и высоте и одинаково отстоящие друг от друга столбики. Принимается условие, что каждый столбик – это общий (итоговый) структурный показатель за отдельный промежуток времени (например, за декаду, месяц, квартал, год и т.д.). Столбики по высоте делят на 100 равных частей, где каждая часть соответствует I %, Следовательно, на диаграмме высота каждой составной части пропорциональна ее удельному весу в составе всего сложного признака. Затем идентичные линии по каждой составной части во всех столбиках с помощью лекала соединяют, в результате чего за весь изучаемый период получаются слои, наглядно показывающие динамику удельных весов в составе сложного признака. Пример слоистой диаграммы представлен на рис. 5.5.
Рис. 5.5. Структура энергетических мощностей в сельскохозяйственной организации «Днепр» (слоистая диаграмма)
Квадратно-сетчатые диаграммы – это равные квадраты, разделенные на 100 одинаковых частей (квадратиков), полученных путем пересекающихся перпендикулярных линий. Это означает, что каждый квадратик равен 1/100 всей площади квадрата, т.е. I % объема сложного признака. Зная удельный вес каждой его составной части, нетрудно определить, сколько квадратиков может она занимать.
Квадратно-сетчатые диаграммы аналогично секторным могут быть использованы при графическом изображении структуры сложных признаков за сравнительно небольшое число периодов иди моментов времени, а также по небольшому количеству статистических единиц или объектов (рис. 5.6).
Рис. 5.6. Структура землепользования в сельскохозяйственной организации «Днепр» (квадратно-сетчатая диаграмма): 1 – с.-х. земли; 2 – не с.-х. земли
Способы графического изображения показателей сравнения
В широком понимании показатели сравнивают и во времени, и в пространстве, т.е. приемами сравнения могут быть охвачены и динамика, и структура, и территориальные объекты. Поэтому при графическом изображении показателей сравнения можно использовать разнообразные приемы; часть из них была рассмотрена выше. Вместе с тем для наглядного изображения абсолютных и относительных показателей сравнения могут быть применены столбиковые, ленточные (полосовые), квадратные, круговые, прямоугольные, фигурные и другие виды диаграмм.
Столбиковая диаграмма – способ графического изображения статистических показателей в форме вертикальных прямоугольников – столбиков, равных по основанию и размещенных рядом или на одинаковом расстоянии друг от друга. Их высота в соответствии с принятым масштабом пропорциональна изображаемым однородным статистическим показателям. При построении столбиковых диаграмм вертикальная масштабная шкала всегда начинается с нулевой отметки и поэтому разрыв масштабной шкалы недопустим.
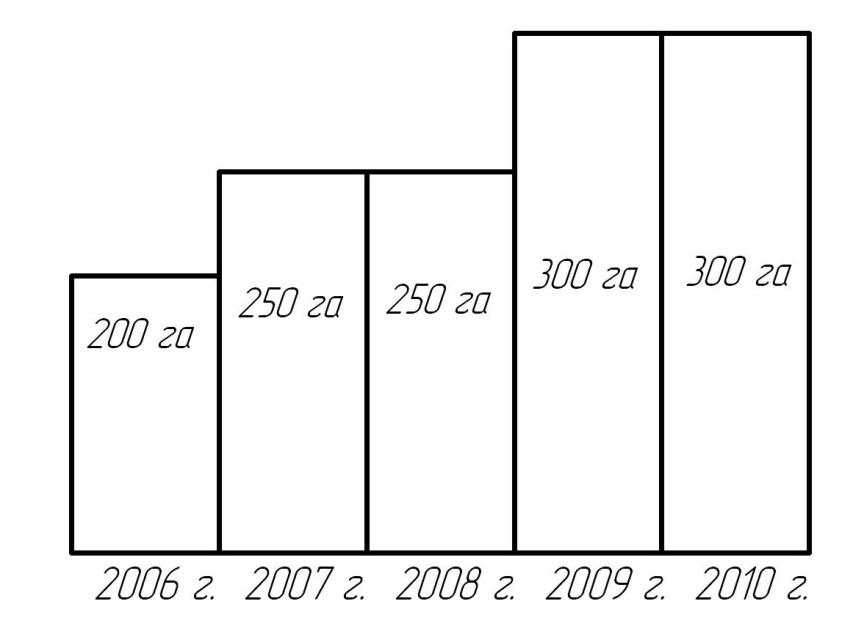
При выборе вертикального масштаба столбиковых диаграмм за основу принимается размещение максимального статистического показателя, а на масштабной шкале отмечаются и записываются лишь круглые или округленные значения. Пример применения столбиковой диаграммы показан на рис. 5.7.
Рис. 5.7. Динамика площади землепользования крестьянского (фермерского) хозяйства «Колос» (столбиковая диаграмма)
Ленточная (полосовая) диаграмма представляет собой графическое изображение сравниваемых показателей в форме прямоугольников – полос одинаковой ширины, располагаемых горизонтально. Отличие от столбиковой лишь в том, что прямоугольники, несущие сравниваемые статистические показатели, размещены не вертикально, а горизонтально.
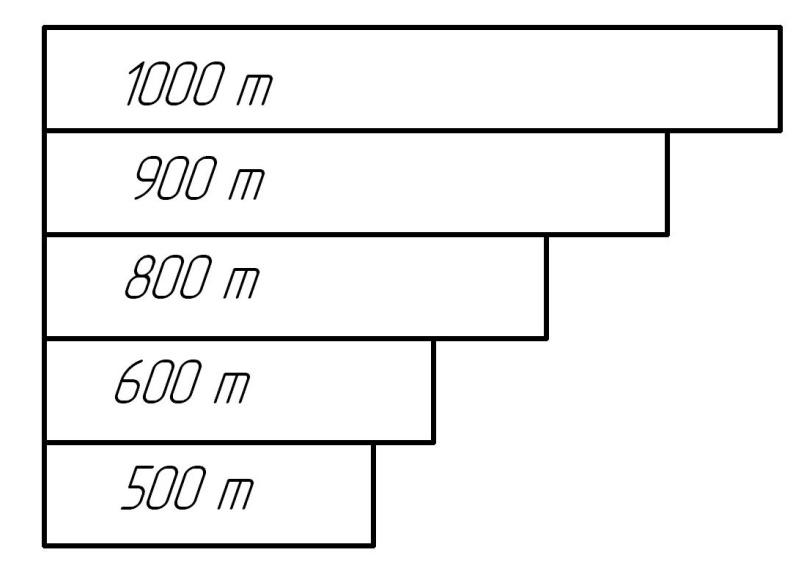
В ленточной диаграмме начало полос должно находиться на одной и той же вертикальной линии, а длина полос по масштабу пропорциональна величине сравниваемых однородных показателей. В качестве примера ленточной (полосовой) диаграммы можно графически показать объем переработки молочного сырья в пяти промышленных организациях (рис. 5.8).
Рис. 5.8. Объёмы переработки молочного сырья в промышленных организациях АПК (ленточная диаграмма)
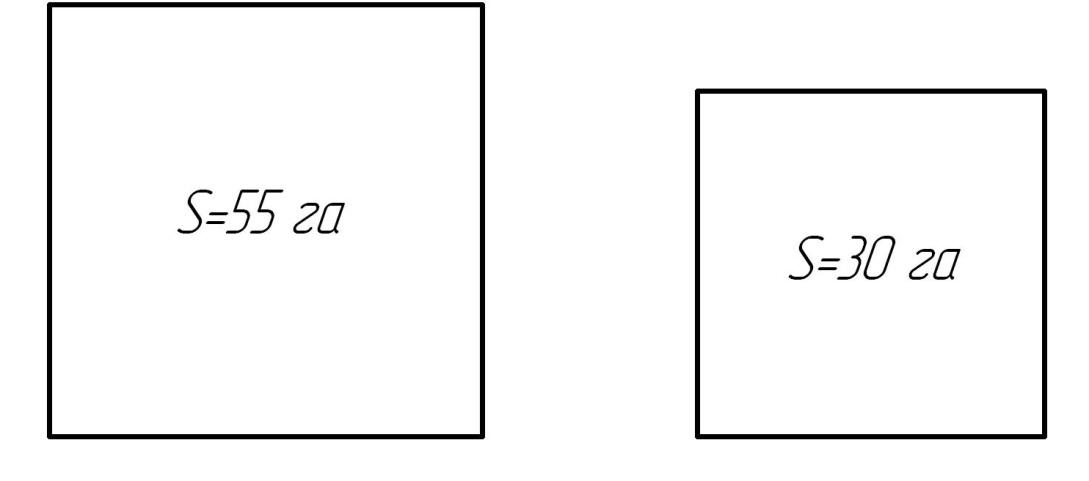
Квадратная диаграмма – один из способов графического изображения сравниваемых однородных показателей, главным образом, абсолютных. В основу ее построения кладутся квадраты, причем их основание обычно располагается на одной, как правило, горизонтальной линии, а число квадратов равно числу изображаемых статистических единиц или объектов. Длина стороны каждого квадрата рассчитывается в следующем порядке: извлекают квадратный корень из диаграммируемых статистических показателей, а затем рассчитывают горизонтальный масштаб таким образом, чтобы на общей горизонтальной прямой смогли разместиться изображаемые квадраты (рис. 5.9).
Рис.5.9. Посевные площади льна-долгунца в подразделениях СПК «Днепр» (квадратные диаграммы)
Способ квадратных диаграмм позволяет графически изобразить довольно большое число сравниваемых статистических единиц или объектов.
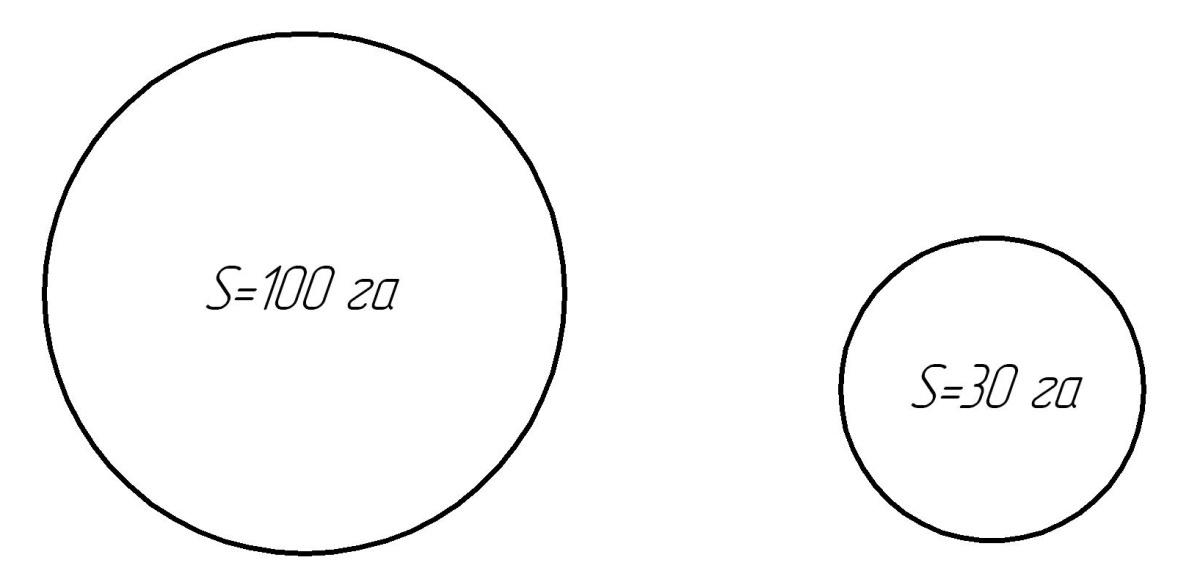
Круговая диаграмма основана на использовании площади кругов для наглядного показа сравниваемых однородных, преимущественно абсолютных, величин друг с другом. При их построении необходимо иметь в виду, что площади кругов соотносятся между собой как квадраты их радиусов. Поэтому при расчете длины радиуса в каждом круге надо прежде всего извлечь квадратный корень из диаграммируемых статистических показателей, а затем, выбрав по радиусам удобный для размещения всех кругов масштаб, с помощью циркуля построить каждый круг. Целесообразно все круги размещать на общей касательной горизонтальной линии.
Подобно квадратным графикам, способ круговых диаграмм позволяет наглядно показать значительное число сравниваемых статистических единиц или объектов (рис. 5.10).
Рис. 5.10. Посевные площади подсолнечника в подразделениях СПК «Нива» (круговая диаграмма)
Прямоугольные диаграммы применяются при графическом изображении главным образом двухмасштабных сравнений: один масштаб – для основания, другой – для высоты. Такие диаграммы обычно используются в случаях, когда необходимо изобразить и сравнить сочетание абсолютных и относительных показателей, представляющих собой произведение двух связанных между собой величин. Например, показать на диаграмме валовой сбор продукции как произведение посевной площади и урожайности культур; валовой надой молока – произведение поголовья коров и их продуктивности; объем грузоперевозочных работ (в тонно-километрах) – произведение количества грузов (т) и расстояние перевозки (км.).
При графическом изображении такого рода сложных показателей с помощью прямоугольных диаграмм несложно показать и их составляющие (сомножители). С этой целью поступают следующим образом: один показатель (обычно независимую переменною величину) согласно масштабу размещают на общей горизонтальной линии, другой (зависимою переменную) также в соответствии с масштабом – по вертикали. Далее, располагая значениями составляющих показателей по каждой статистической единице или объекту, несложно в двух масштабах построить соответствующие прямоугольники, у которых основание – независимый признак, высота – зависимая переменная величина, а площадь каждого подученного прямоугольника – значение сложного показателя.
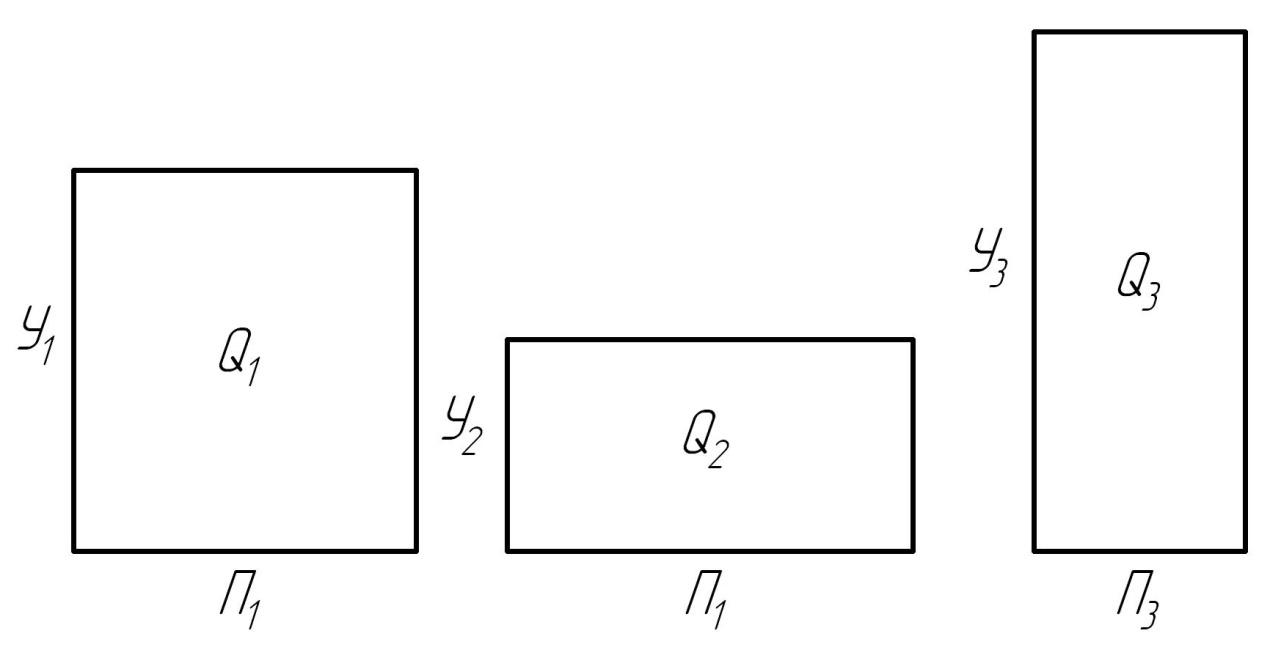
В качестве примера прямоугольной диаграммы можно графически показать одновременное сочетание поголовья коров, их годового удоя и валового производства молока на трех различных фермах сельскохозяйственной организации (рис. 5.11).
Рис. 5.11. Поголовье (П), годовой удой коров (У) и валовое производство молока (Q) в сельскохозяйственных организациях (прямоугольные диаграммы)
Графический показ сложных признаков по способу прямоугольных диаграмм носит название знаков Варзара, так как этот способ был предложен видным русским статистиком В. Е. Варзаром (1851 — 1940гг.) .
Графически взаимосвязи и зависимости между признаками в статистической совокупности можно изобразить с помощью координатной диаграммы, которая, в отличие от линейной, представляет собой точечный график в прямоугольной системе координат. При этом на оси абсцисс откладываются значения независимого (факторного) признака, на оси ординат – значения зависимого (результативного) признака. На площадь, ограниченную осями координат, наносятся точки пересечения координат факторного и результативного показателей, которые соответствуют значениям этих показателей по каждой статистической единице. При этом общее число точек равно числу единиц в статистической совокупности, а полученная в результате графического построения совокупность точек представляет собой поле корреляции. Целесообразно обратить внимание на то, что графическое изображение взаимосвязи между признаками с помощью координатной диаграммы всегда связано с расчетом двух масштабов (на вертикальной и горизонтальной осях). Каждый из этих масштабов можно рассчитать по формуле (5.1).
Графически поле корреляции изображено с помощью координатной диаграммы на примере взаимосвязи доз органических удобрений и урожайности картофеля в 100 крестьянских хозяйствах (рис. 5.12).
Источник