Логический способ представления знаний

1.3.Представление знаний в интеллектуальных системах

Человек одновременно использует самые различные методы представления знаний: языковое описание, графическая информация, математические формулы и т.д. В зависимости от специфики той или иной области деятельности один или несколько видов описания будут превалировать над остальными. Например, в математике формулы и графики будут преобладать над текстовой информацией, в юриспруденции доминирует текстовая информация, в искусствоведении преобладает текстовая и графическая информация. В случае выбора средств представления знаний в технических системах такой универсализм представления знаний невозможен, поскольку потребует аппаратной и программной реализации интеллектуальных функций, недостижимых в настоящее время. Поэтому, существует несколько базовых специализированных машинных языков представления знаний, каждый из которых наиболее предпочтителен для той или иной предметной области [10] — [14] .

1) Язык продукционных правил.

Продукционные правила – это правила, имеющие форму: ЕСЛИ «Условие» – ТО «Событие». Продукционные правила описывают знания в виде взаимосвязей типа: «причина» – «следствие», «явление» – «реакция», «признак» – «факт» и.т.п. Конкретизация продукционных правил меняется в зависимости от сущности представляемых знаний.

• ЕСЛИ «Температура в реакторе превышает 120 ° C » ТО «Снизить подачу топлива на 5%»;
• ЕСЛИ «Вышел из строя вентилятор кондиционера» ТО «Температура в помещении повышается»;

Продукционное представление знаний с человеческой точки зрения является прямым описанием логических выводов при решении конкретных задач. Совокупность знаний о конкретной предметной области в этом случае представляется соответствующим набором продукционных правил, который образует базу знаний. При построении продукционных правил допустимо использование логических операторов И, ИЛИ, например:

• ЕСЛИ «Температура в реакторе превышает 120 ° C » И «Температура хладагента превышает 90 ° C » ТО «Прекратить подачу топлива»;
• ЕСЛИ «Температура в реакторе превышает 90 ° C » ИЛИ «Температура хладагента превышает 60 ° C » ТО «Снизить подачу топлива на 40%».

Недостатком языка продукционных правил можно считать отсутствие явных связей между правилами и целями, к достижению которых необходимо стремится. Таким образом, для активизации одного из продукционных правил необходимо проверка всей продукционной базы знаний, что при больших объемах информации приводит к существенным затратам временных и технических ресурсов интеллектуальной системы. Возможность решения этой проблемы заключается в разработке перспективных продукционных баз знаний, в которых одни продукционные правила могут активировать и дезактивировать другие продукционные правила, влияя на количество перебираемых правил в текущем цикле и, следовательно, на выбор пути достижения цели управления.

Отличительной чертой и основным преимуществом продукционной базы знаний является простота анализа, дополнения, модификации и аннулирования определенных продукционных правил. Помимо этого, представление знаний в таком синтаксически однотипном виде существенно облегчает техническую реализацию системы использования знаний. Вследствие этого в настоящее время продукционные базы знаний получили наибольшее распространение в интеллектуальных технических системах.

2) Язык семантических сетей.

Знаниями можно назвать описания отношений между абстрактными понятиями и сущностями, являющимися конкретными объектами реального мира. Изначально семантические сети разрабатывались как модели долговременной человеческой памяти в психологии, но впоследствии эта модель перекочевала в инженерию знаний. В семантической сети абстрактные понятия и отношения между ними описываются в виде узлов и дуг. Сущности и понятия в такой сети являются узлами, а отношения между ними – дугами. Атрибуты семантических сетей можно разделить на лингвистические (объект, условие, место, инструмент, цель и т.п.), атрибутивные (форма, размер, цвет и т.п.), характеристические (род, время, наклонение и т.п.), логические (да, нет, отрицание, объединение и т.п.).

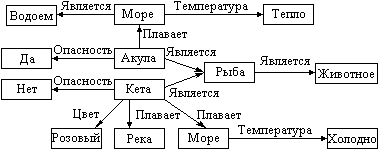
Рис.1.5. Семантическое представление знаний биолога

Допустим, фрагмент знаний ихтиолога о биологии рыб можно описать следующей семантической сетью (рис.1.5). В качестве другого примера рассмотрим представление знаний, содержащихся в высказывании: «Робот сверлит отверстие в детали с помощью сверла 10» (рис.1.6).

Рис.1.6. Семантическое представление технического знания

Недостаток семантических сетей – дублирование информации при построении сетей и смешение групп знаний, относящихся к различным ситуациям. Например, семантическая сеть, представленная на рис.1.5, имеет дубляж понятия «море», а отношение «температура» может использоваться не только для описания среды обитания животных. Выходом из данной ситуации стала наметившаяся в последнее время тенденция к построению разделенных семантических сетей.

Основным преимуществом семантических сетей является то, что они имитируют понимание и использование человеком естественного языка, что позволяет применять их при техническом моделировании рассуждений, доказательстве теорем, построении незаданных явно причинно-следственных связей и лингвистических конструкций, т.е. семантические сети позволяют реализовать устройства, имитирующие мыслительные акты более высокого уровня по сравнению с продукционными правилами. Представление знаний в виде семантических сетей широко используется в интеллектуальных системах интерпретации естественного языка и автоматического машинного перевода, в диалоговых вопросно-ответных системах естественного человеко-машинного общения, в блоках логической интерпретации систем технического зрения.

3) Язык логики предикатов.

Логика предикатов является разделом математики – математической логикой, имеющей большую историю. Данная область математики традиционно составляла математический фундамент, закладываемый в основу формального описания систем. В качестве примера построения и вывода знаний на языке логики предикатов достаточно привести известный силлогизм Сократа: Все люди – смертны, человек – один из людей, Сократ – человек, следовательно Сократ – смертен.

Основные положения логики предикатов заключаются в следующем. Допустим, имеется некоторое множество объектов, составляющих предметную область, знания о которой необходимо описать. Произвольные элементы этого множества называются предметными переменными x i , а конкретные элементы этого множества, называются предметными константами y i . Выражение P x 1 , x 2 , … , x n , зависящее от предметных переменных и принимающее значение «0»-(ложь) или «1»-(истина), называется логической функцией или предикатом. Выражение P y 1 , y 2 , … , y m , зависящее от предметных констант и принимающее значение «0»-(ложь) или «1»-(истина), называется элементарной формулой. Из элементарных формул с помощью логических связок « ∧ »-(И), « ∨ »-(ИЛИ), « ¬ »-(отрицание), « -(импликация), « ↔ »-(эквивалентность) строятся предикатные формулы. Помимо логических связок в рассмотрение вводят квантор общности и квантор существования « ∃ ». Знания о конкретной предметной области будут описываться предикатами и предикатными формулами. Для организации логического вывода « ↦ »-(символ выводимости) на языке логики предикатов используются различные правила. Например, правило Moduspones ( A → B , A ↦ B ) – если из A следует B и если A является логически непротиворечивой предикатной формулой, то B также является логически непротиворечивой предикатной формулой. В качестве примера рассмотрим основной набор базовых действий и производных правил поведения транспортного робота-тележки, записанные на языке исчисления предикатов:

A — «накопитель готовых деталей около станка пуст»;

B -«тележка транспортного робота пуста»;

C -«освободить накопитель готовых деталей около станка»;

D -«перейти к следующему станку»;

E -«отвезти детали на склад, освободить тележку робота»;

F -«вернуться к текущему станку»;

Основной недостаток языка логики предикатов при представлении знаний состоит в ограниченной выразимости, поскольку существует множество фактов и взаимосвязей, которые тяжело или даже невозможно выразить средствами математической логики. Например, такое логичное с точки зрения человека умозаключение, как «Человек колет дрова топором, топор – острый, следовательно человеку колоть дрова легко», на языке логики предикатов непредставимо, поскольку содержит так называемый сценарный, а не логический вывод.

Преимущество логики предикатов при представлении знаний заключается в том, что данный способ обладает хорошо развитым и понятным математическим аппаратом. Логика предикатов всесторонне исследована как формальная система. Синтаксис и интерпретация логических функций, элементарных и предикатных формул, правил логического вывода образуют единую стройную теорию математической логики. Это позволяет легко программировать различные операции над знаниями, в том числе логический вывод новых знаний на основе имеющихся знаний. Язык логики предикатов почти так же популярен в технических системах, как и язык продукционных правил, который можно рассматривать как упрощенный язык логики предикатов. Действительно, базовая конструкция языка продукционных правил: ЕСЛИ «причина»/«условие» ТО «следствие»/«действие», по сути является всего лишь одной из логических связок языка логики предикатов – импликацией A → B (из A следует B ). Однако, в отличие от языка логики предикатов, язык продукционных правил обладает одним существенным преимуществом – полной независимостью элементов базы знаний, поскольку отдельные продукционные правила логически не связаны между собой. Это, несмотря на некоторые осложнения при обработке знаний, обусловленные опасностью нарушения их целостности и непротиворечивости, позволяет языку продукционных правил охватить больший круг различных предметных областей за счет возможности описания знаний, опирающихся не на логические, а на традуктивные и сценарные выводы [1] , [10] , [13] . Поэтому по частоте использования в интеллектуальных системах язык логики предикатов на данный момент все таки немного уступает языку продукционных правил.

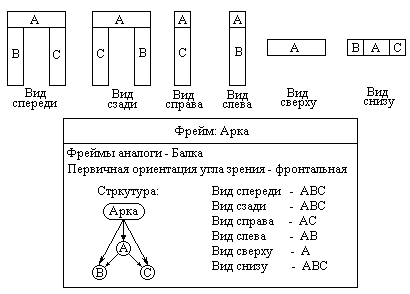
Фреймовая система представления знаний является моделью описания человеческих знаний в виде связанной совокупности крупных структурных единиц, каждая из которых содержит данные, описывающие определенную ситуацию. Во фреймовой системе единицей представления является объект, называемый фреймом. Фрейм содержит совокупность некоторых понятий и сущностей, с помощью которой можно описать конкретную ситуацию. Фрейм имеет уникальное имя и внутреннюю структуру, состоящую из множества упорядоченных элементов – слотов. Каждый слот имеет уникальное в пределах своего фрейма имя и содержит определенную информацию. Таким образом, каждый фрейм это структура данных, описывающая определенную ситуацию, место, объект и т.п. Структура данных внутри фрейма может иметь различный вид: граф, таблица и т.п., а также может представлять комбинацию различных способов представлений данных. Фреймы могут быть связаны между собой посредством своих слотов и образовывать иерархические структуры. Например, в системе технического зрения, имеющей три пары независимо пространственно ориентированных датчиков, составная арка может быть представлена в виде следующего фрейма (рис.1.7):

Рис.1.7. Фрейм, описывающий различные ракурсы обзора арки.

Описание арки таким фреймом, позволяет распознавать арку и ее ориентацию в системах технического зрения. Допустим, система технического зрения оценивает панораму арки при виде сверху. Результат оценки – «А». Далее система начинает сличать оценку «А» со значениями различных слотов в различных фреймах и составлять список фреймов- кандидатов на идентификацию детали. Результатом отбора будут описывающие различные конструкции фреймы, содержащие слот со значением «А». Системе остается изменить угол зрения, оценить новую панорамную картину и сузить список фреймов, проверяя на соответствие новому значению слоты первоначально отобранных фреймов. К примеру, фрейм – балка выпадет из списка после первой же процедуры отсева, поскольку как балку не крути, результат оценки панорамы всегда будет – «А». Последовательно повторяя этот процесс, можно идентифицировать деталь абсолютно точно (по всем шести ракурсам) или с определенной степенью вероятности (если ракурсов анализа меньше). Машина может идти и по другому пути анализа: не составлять список фреймов-кандидатов, а остановиться на первом попавшемся подходящем фрейме и провести сравнительную оценку всех ракурсов детали с соответствующими слотами фрейма. Если хотя бы один из слотов текущего фрейма противоречит оценке панорамы, то анализу подвергается фрейм-аналог и т.д., пока при движении по цепочке фреймов не будет достигнуто совпадение всех ракурсов, или их наибольшего числа.

Недостатком фреймовой системы является то, что иерархическая сеть знаний с перекрестными ссылками пригодна для решения сравнительно простых проблем, поскольку при расширении проблемной области фреймовая сеть имеет свойство разрастаться до значительных размеров. Проблемы поиска решения в таких сетях становятся трудноразрешимыми, поскольку связи между фреймами в сетях, описывающих объемные знания, как правило, неоднозначны и устанавливаются по нескольким слотам. Кроме того, фреймовые сети менее приспособлены к адаптации, так как внесение новых фреймов и измерение слотов в имеющихся фреймах может повлечь противоречия и зацикливания в ссылках при движении по иерархической структуре фреймовой сети.

Достоинством фреймового языка представления знаний является то, что он предоставляет пользователю большую свободу при описании знаний, так как допускает различные способы описания данных в пределах одного фрейма. Благодаря этому, фреймовые системы можно отнести к самым универсальным системам описания знаний. Однако ограничение сложности решаемых на основе таких систем проблем пока не позволяет фреймовым системам доминировать при разработке интеллектуальных систем.

Источник

Представления знаний в интеллектуальных системах, экспертные системы

Введение

Экспертная система (далее по тексту — ЭС) — это информационная система, назначение которой частично или полностью заменить эксперта в той или иной предметной области. Подобные интеллектуальные системы эффективно применяются в таких областях, как логистика, управление воздушными полетами, управление театром военных действий. Основною направленной деятельностью предсказание, прогнозирование в рамках определенного аспекта в предметной области.

Экскурс в историю экспертных систем

История экспертных систем берет свое начало в 1965 году. Брюс Бучанан и Эдвард Фейгенбаум начали работу над созданием информационной системы для определения структуры химических соединений.

Результатом работы была система под названием Dendral. В основе системы формировалась последовательность правил подобных к «IF – THEN». Информационная система не перестала развиваться и получила множество наследников, таких как ONCOIN – информационная система для диагностики раковых заболеваний, MYCIN – информационная система для диагностики легочных инфекционных заболеваний.

Следующим этапом стали 70-е годы. Период не выделялся особыми разработками. Было создано множество разных прототипов системы Dendral. Примером служит система PROSPECTOR, областью деятельности которой являлась геологические ископаемые и их разведка.
В 80-ых годах появляются профессия – инженер по знаниям. Экспертные системы набирают популярность и выходят на новый этап эволюции интеллектуальных систем. Появились новые медицинские системы INTERNIS, CASNE.

С 90-ых годов развитие интеллектуальных систем приобретает новые и новые методы и особенности. Нововведением становится парадигма проектирования эффективных и перспективных систем. Гибкость, четкость решения поставленных задач дало новое название – мультиагентных систем. Агент – фоновый процесс который действует в целях пользователя. Каждый агент имеет свою цель, «разум» и отвечает за свою область деятельности. Все агенты в совокупности образуют некий интеллект. Агенты вступают в конкуренцию, настраивают отношения, кооперируются, все как у людей.

В 21 век, интеллектуальной системой уже не удивишь никого. Множество фирм внедряет экспертные системы в области своей деятельности.

Быстродействующая система OMEGAMON разрабатывается c 2004 года с IBM, цель которой отслеживание состояния корпоративной информационной сети. Служит для моментального принятия решений в критических или неблагоприятных ситуациях.

G2 – экспертная система от фирмы Gensym, направленная на работу с динамическими объектами. Особенность этой системы состоит в том, что в нее внедрили распараллеливание процессов мышления, что делает ее быстрее и эффективней.

Структура экспертной системы

1. База знаний
Знания — это правила, законы, закономерности получены в результате профессиональной деятельности в пределах предметной области.
База знаний — база данных содержащая правила вывода и информацию о человеческом опыте и знаниях в некоторой предметной области. Другими словами, это набор таких закономерностей, которые устанавливают связи между вводимой и выводимой информацией.

2. Данные
Данные — это совокупность фактов и идей представленных в формализованном виде.
Собственно на данных основываются закономерности для предсказания, прогнозирования. Продвинутые интеллектуальные системы способные учиться на основе этих данных, добавляя новые знания в базу знаний.

3. Модель представления данных
Самая интересная часть экспертной системы.
Модель представления знаний (далее по тексту — МПЗ) — это способ задания знаний для хранения, удобного доступа и взаимодействия с ними, который подходит под задачу интеллектуальной системы.

4. Механизм логического вывода данных(Подсистема вывода)
Механизм логического вывода(далее по тексту — МЛВ) данных выполняет анализ и проделывает работу по получению новых знаний исходя из сопоставления исходных данных из базы данных и правил из базы знаний. Механизм логического вывода в структуре интеллектуальной системы занимает наиболее важное место.
Механизм логического вывода данных концептуально можно представить в виде :
А — функция выбора из базы знаний и из базы данных закономерностей и фактов соответственно
B — функция проверки правил, результатом которой определяется множество фактов из базы данных к которым применимы правила
С — функция, которая определяет порядок применения правил, если в результате правила указаны одинаковые факты
D — функция, которая применяет действие.

Какие существуют модели представления знаний?

Распространены четыре основных МПЗ:

• Продукционная МПЗ
• Семантическая сеть МПЗ
• Фреймовая МПЗ
• Формально логическая МПЗ

Продукционная МПЗ

В основе продукционной модели представления знаний находится конструктивная часть, продукция(правило):
IF , THEN
Продукция состоит из двух частей: условие — антецендент, действие — консеквент. Условия можно сочетать с помощью логических функций AND, OR .
Антецеденты и консеквенты составленных правил формируются из атрибутов и значений. Пример: IF температура реактора подымается THEN добавить стержни в реактор
В базе данных продукционной системы хранятся правила, истинность которых установлена к за ранее при решении определенной задачи. Правило срабатывает, если при сопоставлении фактов, содержащихся в базе данных с антецедентом правила, которое подвергается проверке, имеет место совпадение. Результат работы правила заносится в базу данных.

Пример

Диагноз	Температура	Давление	Кашель
Грипп	39	100-120	Есть
Бронхит	40	110-130	Есть
Аллергия	38	120-130	Нет

Пример продукции:
IF Температура = 39 AND Кашель = Есть AND Давление = 110-130 THEN Бронхит

Продукционная модель представления знаний нашла широкое применение в АСУТП

Среды разработки продукционных систем(CLIPS)

CLIPS (C Language Integrated Production System) — среда разработки продукционной модели разработана NASA в 1984 году. Среда реализована на языке С, именно потому является быстрой и эффективной.
Пример:

Подобное правило будет активировано только тогда, когда в базе данных появится факт симптома с подобными параметрами.

Семантическая сеть МПЗ

В основе продукционной модели лежит ориентированный граф. Вершины графа — понятия, дуги — отношения между понятиями.
Особенностью является наличие трех типов отношений:

• класс — подкласс
• свойство — значение
• пример элемента класса

По количеству типов отношений выделяют однородные и неоднородные семантические сети. Однородные имею один тип отношения между всеми понятиями, следовательно, не однородные имею множество типов отношений.

Все типы отношений:

• часть — целое
• класс — подкласс
• элемент — количество
• атрибутивный
• логический
• лингвистический

Пример

Недостатком МПЗ является сложность в извлечении знаний, особенно при большой сети, нужно обходить граф.

Фреймовая МПЗ

Предложил Марвин Мински в 1970 году. В основе фреймовой модели МПЗ лежит фрейм. Фрейм — это образ, рамка, шаблон, которая описывает объект предметной области, с помощью слотов. Слот — это атрибут объекта. Слот имеет имя, значение, тип хранимых данных, демон. Демон — процедура автоматически выполняющаяся при определенных условиях. Имя фрейма должно быть уникальным в пределах одной фреймовой модели. Имя слота должно быть уникальным в пределах одного фрейма.

Слот может хранить другой фрейм, тогда фреймовая модель вырождается в сеть фреймов.

Пример

Пример вырождающейся в сеть фреймов

На своей практике, мне доводилось встречать системы на основе фреймовой МПЗ. В университете в Финляндии была установлена система для управления электроэнергией во всем здании.

Языки разработки фреймовых моделей (Frame Representation Language)

FRL (Frame Representation Language) — технология создана для проектирования интеллектуальных систем на основе фреймовой модели представления знаний. В основном применяется для проектирования вырождающихся в сеть фреймовой модели.

Запись фрейма на языке FRL будет иметь вид:

Существуют и другие среды: KRL (Knowledge Representation Language), фреймовая оболочка Kappa, PILOT/2.

Формально логическая МПЗ

В основе формально логической МПЗ лежит предикат первого порядка. Подразумевается, что существует конечное, не пустое множество объектов предметной области. На этом множестве с помощью функций интерпретаторов установлены связи между объектами. В свою очередь на основе этих связей строятся все закономерности и правила предметной области. Важное замечание: если представление предметной области не правильное, то есть связи между объектами настроены не верно или не в полной мере, то правильная работоспособность системы будет под угрозой.

Пример

A1 = A2 = A3 = ; IF A1 AND A2 THEN
Банальней примера и не придумаешь.
Важно: Стоит заметить, что формально логическая МПЗ схожа с продукционной. Частично это так, но они имеют огромную разницу. Разница состоит в том, что в продукционной МПЗ не определены никакие связи между хранимыми объектами предметной области.

Важно

Любая экспертная система должна иметь вывод данных и последовательность «мышления» системы. Это нужно для того чтобы увидеть дефекты в проектировании системы. Хорошая интеллектуальная система должна иметь право ввода данных, которое реализуется через интеллектуальный редактор, право редактора на перекрестное «мышление» представлений при проектировании системы и полноту баз знаний(реализуется при проектировки закономерностей предметной области между инженером по знаниям и экспертом).

Заключение

Экспертные системы действительно имеют широкое применение в нашей жизни. Они позволяют экономить время реальных экспертов в определенной предметной области. Модели представления знаний это неотъемлемая часть интеллектуальных систем любого уровня. Поэтому, я считаю, что каждый уважающий себя IT-специалист, должен иметь даже поверхностные знания в этих областях.

Источник