Логические задачи табличный способ презентация

ПРЕЗЕНТАЦИЯ Решение логических задач табличным способом. Решение логических задач графическим способом
презентация к уроку по информатике и икт (9 класс) по теме

Презентация к уроку «Решение логических задач табличным способом. Решение логических задач графическим способом»

Скачать:

Вложение	Размер
zadachi.pptx	718.99 КБ

Предварительный просмотр:

Подписи к слайдам:

РЕШЕНИЕ ЛОГИЧЕСКИХ ЗАДАЧ ТАБЛИЧНЫМ И ГРАФИЧЕСКИМ СПОСОБОМ учитель информатики и ИКТ Н.Л. Никитенко

Английский математик, писатель и логик Чарльз Доджсон (Льюис Кэрролл): «Своенравная и непокорная логика отныне укрощена и обуздана». ГРАФИЧЕСКИЙ МЕТОД

ГРАФИЧЕСКИЙ МЕТОД http://to-name.ru/biography/ljuis-kerrol.htm

Лёня, Женя и Миша имеют фамилии Орлов, Соколов и Ястребов. Какую фамилию имеет каждый мальчик, если Женя, Миша и Соколов — члены математического кружка, а Миша и Ястребов занимаются музыкой. Ответ: Лёня Соколов, Миша Орлов, Женя Ястребов ГРАФИЧЕСКИЙ МЕТОД Лёня Женя Миша Орлов Соколов Ястребов

В редакцию журнала прислали рассказ, повесть, очерк, стихотворение и фельетон, которые написали Анискин , Борискин, Вискин , Грискин и Денискин. Каждый написал только одно произведение. Вискин думал, что стихотворение сочинил Борискин. Борискин предполагал, что Грискин написал фельетон, а Анискин — повесть. Грискин считал, что Денискин написал повесть, а Вискин — очерк. Анискин думал, что Борискин написал рассказ, а стихотворение сочинил Грискин . В результате оказалось, что все они ошибались в своих предположениях. Кто что написал? ГРАФИЧЕСКИЙ МЕТОД Д Б А В Р П С О Г Ф

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А Б В Г Д Е

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + Б + В Г Д + Е

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + Б + + В Г + Д + Е

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + Б + + В + Г + Д + Е

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + + Б + + В + + Г + Д + + Е +

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + + + Б + + + В + + + Г + Д + + Е +

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + — + + Б + + + В — + + + Г — 1 — — — Д + — + Е — +

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + — + + Б + + — + В — + + + Г — 1 — — — Д + — + Е — — — 1 —

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + — — + + Б + + — — + В — — 1 + + Г — 1 — — — Д + — — + — Е — — — 1 —

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + — — + + Б + + — — + В — — 1 + + Г — 1 — — — Д 1 — — + — Е — — — 1 —

Друзья Миша, Иван, Веня, Юра и Дима должны поехать в разные города А, Б, В, Г, Д, Е. При этом: Миша может ехать только в А, Б, Д; Иван может ехать только в Б и Г; Веня может ехать только один и в В; Юра не может ехать вместе с Иваном; Дима может ехать только с Мишей и Веней, но не в Д. В каком городе мог быть каждый из них, если оказалось, что вдвоем они не были ни в одном городе. Дима может ехать в А или Б, так как туда никто не едет. ТАБЛИЧНЫЙ МЕТОД Миша Иван Веня Юра Дима А + — — + 1 Б + + — — 1 В — — 1 + + Г — 1 — — — Д 1 — — + — Е — — — 1 —

1. Найти ошибку в решении задачи: В один ряд стоят 5 домов, в которых живут люди разных национальностей. Француз выращивает яблони. Ему 40 лет. Тот, кто живет в центре, играет на скрипке. Англичанин выращивает груши. Швед, который играет на трубе, живет сразу слева от 40-летнего. Сразу справа от 45-летнего живет тот, который занимается плаванием. Немец – прыгун в длину. 30-летний и играющий на рояле — соседи. В саду у теннисиста растут черешни. Поляк выращивает вишни и живет непосредственно правее от того, кто увлекается плаванием. Тот, кто играет на ударных — бегун. Гитарист – сосед того, в саду которого вишни. 35-летний живет с краю. Скрипач выращивает абрикосы. 30-летний и 35-летний – ближайшие соседи и очень дружны. Бегун всегда совершает утреннюю пробежку по своему яблоневому саду. Кому из них 50 лет? Кто играет в гольф? 2. Дорисуйте необходимые связи между объектами и дайте ответ ЗАДАНИЕ ГРУППАМ

РЕШЕНИЕ ЗАДАЧИ 1 скрипка рояль труба ударные гитара француз + немец + поляк + швед + англичанин +

РЕШЕНИЕ ЗАДАЧИ 2

Задача: Однажды в лагере за круглым столом оказалось пятеро ребят из Перми, Соликамска, Кунгура, Чернушки и Осы: Юра, Толя, Леша, Коля и Витя. Пермяк сидел между осинцем и Витей, соликамец – между Юрой и Толей, а напротив него сидели Чернушанин и Алеша. Коля никогда не был в Соликамске, а Юра не был в Перми и Осе, осинец с Толей регулярно переписываются в « аське ». Определить, в каком городе живет каждый из ребят? ДОМАШНЕЕ ЗАДАНИЕ

Источник

Презентация на тему «Решение логических задач методом таблиц»

В данной презентации содержатся 5 логических задач с решениями.

Содержимое разработки

Логика: орудие, используемое для обоснования предубеждений. Элберт Хаббард

Решение логических задач

Разработал: Учитель информатики и ИКТ Такиуллин Ришат Ринатович

В логических задачах нет игры слов, нет попыток ввести вас в заблуждение.

Для их решения не нужны сложные вычисления, знания формул и теорем.

Найти верные ответы вам помогут смекалка и логика.

Решение логических задач можно сравнить с решением научной проблемы.

Вначале исследователь располагает многими данными, на первый взгляд никак не связанными между собою.

В ходе анализа этих данных выдвигаются и сопоставляются с фактами новые и новые гипотезы.

И вот, наконец, одна из гипотез совпадает с результатами экспериментов и наблюдений.

Разрозненные данные сливаются в целостную картину.

Становится ясно, что найденное объяснение фактов является единственно возможным.

Похожим методом ищут ответы на логические задачи.

Единого правила их решения нет.

Задачи разнообразны, как разнообразны и описываемые в них ситуации, но есть некоторые общие приемы, помогающие проводить анализ задач.

Так, например, трудно удержать в памяти все звенья логических рассуждений.

Испытанный способ их записи – составление таблиц, называемых логическими квадратами.

Как они строятся?

Объясним на несложном примере:

Логическая задача №1

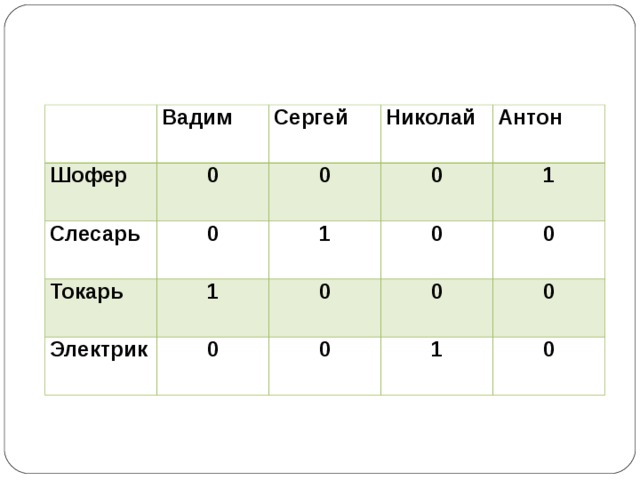
• В одном дворе живут четыре друга. Вадим и шофёр старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.

Источник

Презентация «Табличный способ решения логических задач»

Описание презентации по отдельным слайдам:

Предмет математики настолько серьезен, что нельзя упускать случая сделать его немного занимательным. Блез Паскаль

Эмблема мастер-класса: Говорят уравнение вызывает сомнение, но итогом сомнения может быть озарение!

Основные приемы и методы решения логических задач Теория, мой друг, суха, но зеленеет жизни древо. И.В.Гете Известно несколько различных способов решения логических задач: Метод рассуждений; Метод таблиц; Метод графов; Метод блок-схем; Метод бильярда; Метод кругов Эйлера.

Остановимся подробно на табличном способе решения логических задач

Решение логических задач табличным способом Задача 1. В симфонический оркестр приняли на работу трёх музыкантов: Брауна, Смита и Вессона, умеющих играть на скрипке, флейте, альте, кларнете, гобое и трубе. Известно, что: 1. Смит самый высокий; 2. играющий на скрипке меньше ростом играющего на флейте; 3. играющие на скрипке и флейте и Браун любят пиццу; 4. когда между альтистом и трубачом возникает ссора, Смит мирит их; 5. Браун не умеет играть ни на трубе, ни на гобое. На каких инструментах играет каждый из музыкантов, если каждый владеет двумя инструментами?

Решение 1. Смит самый высокий; 2. играющий на скрипке меньше ростом играющего на флейте; 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун Смит Вессон

Решение 3. играющие на скрипке и флейте и Браун любят пиццу; 0 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун Смит 0 Вессон

Решение 4. когда между альтистом и трубачом возникает ссора, Смит мирит их; 0 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 Смит 0 Вессон

Решение 5. Браун не умеет играть ни на трубе, ни на гобое. 0 0 1 1 0 Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 Смит 0 0 0 Вессон

Решение Так как музыкантов трое, инструментов шесть и каждый владеет только двумя инструментами, получается, что каждый музыкант играет на инструментах, которыми остальные не владеют. 1 1 1 1 0 0 0 0 Ответ: Браун играет на альте и кларнете, Смит — на флейте и гобое, Вессон — на скрипке и трубе. Скрипка Флейта Альт Кларнет Гобой Труба Браун 0 0 1 1 0 0 Смит 0 0 0 0 Вессон

Задача 2 На конгрессе встретились четверо ученых: физик, биолог, историк и математик. Каждый учёный владел двумя языками из четырёх (русским, английским, французским и итальянским), но не было такого языка, на котором могли бы разговаривать все четверо. Есть только один язык, на котором могли вести беседу сразу трое. 1.Никто из учёных не владеет и французским, и русским языками. 2. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 4. Физик, биолог и математик могут разговаривать на одном языке. Какими двумя языками владеет каждый учёный?

1.Никто из учёных не владеет и французским, и русским языками. 2. Хотя физик не говорит по-английски, он может служит переводчиком, если историк и биолог захотят побеседовать. Решение 0 Языки профессия Русский Аанглийский Французский Итальянский Математик Биолог Физик Историк

Решение 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 4. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 0 1 1 0 Языки профессия Русский Английский Французский Итальянский Математик Биолог Физик 0 Историк

Решение 4. Физик, биолог и математик могут разговаривать на одном языке. 1.Никто из учёных не владеет и французским, и русским языками. 0 0 Языки профессия Русский Английский Французский Итальянский Математик 0 Биолог 0 Физик 1 0 Историк 1

Решение 4. Физик, биолог и математик могут разговаривать на одном языке. Какими двумя языками владеет каждый учёный? 1 1 1 1 Языки профессия Русский Английский Французский Итальянский Математик 0 Биолог 0 Физик 1 0 0 Историк 1 0 0

Решение 2. Хотя физик не говорит по-английски, он может служить переводчиком, если историк и биолог захотят побеседовать. 3. Историк говорит по-русски и может говорить с математиком, хотя тот не знает ни одного русского слова. 0 1 0 1 Ответ: математик – английский и итальянский; биолог – французский и итальянский; физик – русский и итальянский; историк – русский и английский. Языки профессия Русский Английский Французский Итальянский Математик 0 1 Биолог 0 1 Физик 1 0 0 1 Историк 1 1 0 0

Алгоритм решения Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты. 2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов. 3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок. 4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия. 5. Решение можно найти простым методом последовательных исключений.

Тренировочные задания Три одноклассника — Влад, Тимур и Юра, встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой физиком, а третий юристом. Один полюбил туризм, другой бег, страсть третьего — регби. Юра сказал, что на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист. Врач сказал, что он разделяет увлечение коллеги. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен. Определите, кто чем любит заниматься в свободное время и у кого какая профессия.

Ответ на задачу Имя Юра Тимур Влад Профессия Увлечение

Ответ на задачу Имя Юра Тимур Влад Профессия физик врач юрист Увлечение бег туризм регби

“Смотреть – не значит видеть!” k = n = m = 1 4 7

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 821 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 290 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-052911

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник