- Решение логических задач с помощью таблиц учебно-методический материал по информатике и икт (7 класс) на тему
- Скачать:
- Предварительный просмотр:
- Урок 17 Табличное решение логических задач
- Практическая работа №6 «Создаем табличные модели» (задания 7 — 9)
- Табличное решение логических задач
- Пример 1
- Пример 2
- Коротко о главном
- Вопросы и задания
- Практическая работа №6 «Создаем табличные модели» (задания 7 — 9)
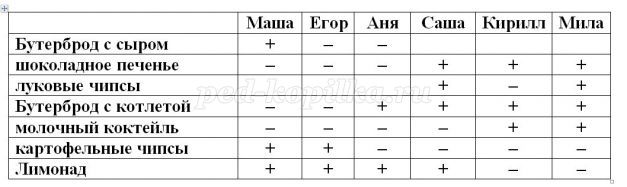
- Задание 7. Логическая задача
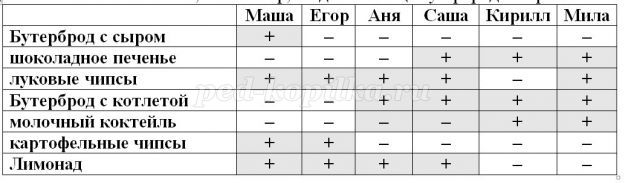
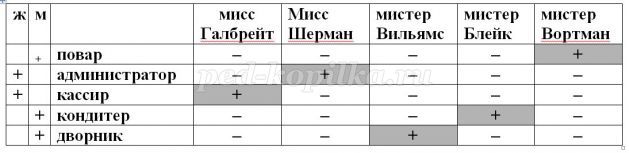
- Задание 8. Самые-самые
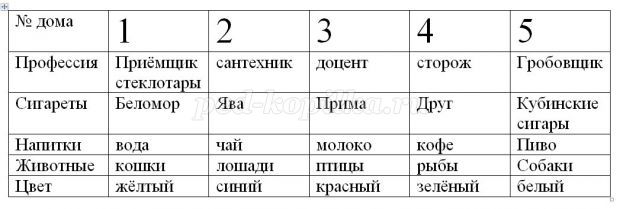
- Задание 9. Творческое задание
- Решение логических задач табличным способом
Решение логических задач с помощью таблиц
учебно-методический материал по информатике и икт (7 класс) на тему
Данный материал можно использовать в 7 классе при изучении темы «Решение логических задач с помощью таблиц» . Материала позволяет расширить представления учащихся о табличных информационных моделях, закрепить представление о табличном способе решения логических задач, закрепить навыки создания таблиц
Скачать:
| Вложение | Размер |
|---|---|
| zadachi_tablichnye.docx | 25.66 КБ |
Предварительный просмотр:
Учебно-методическое пособие.»Табличное решение логических задач. 7 класс»
Напрушкина Е.С. учитель математики и информатики ГБОУ СОШ№136.
Вся наша жизнь это непрерывное решение больших и маленьких логических проблем. Без умения логически думать, рассуждать, делать выбор жить трудновато.
Основной смысл в решении логической задачи состоит в том, чтобы как следует разобраться в условии, распутать все связи между участвующими объектами. В первую очередь, логика отвечает за упорядочивание мыслей. Отсюда можно сказать, что логические задачи – задачи, в первую очередь, на установление порядка
В данном пособие рассматривается прием, который используется при решении текстовых логических задач, — построение таблиц . Таблицы помогают делать правильные логические выводы в ходе решения задачи и позволяют наглядно представить условие задачи или ее ответ.
Но этот прием не обладает универсальностью, т.к. предназначен для решения только одного типа задач. Построение таблицы требует анализа находящейся в ней информации, умения сравнивать и сопоставлять.
Первый шаг решения задачи — это специально составленная таблица .
Далее в таблице отражается условие задачи. Ячейки таблицы заполняются цифрами 0 и 1 в зависимости от того, ложно («0») или истинно («1») соответствующее высказывание.
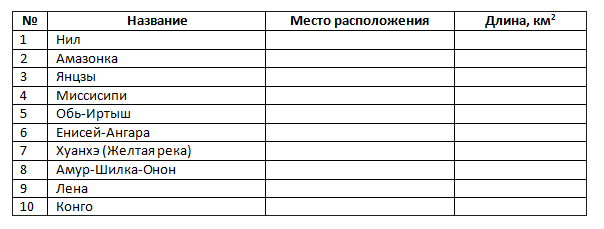
В данной разработке представлены задачи, решаемые табличным способом. Учащиеся могут решать задачи как с помощью ПК, так и в тетрадях. Всего представлено 10 задач, учащиеся сами выбирают 3 задачи, которые они могут решить,
В одном дворе живут четыре друга. Вадим и шофёр старше Сергея; Николай и слесарь занимаются боксом; электрик – младший из друзей; по вечерам Антон и токарь играют в домино против Сергея и электрика. Определите профессию каждого из друзей.
Источник
Урок 17
Табличное решение логических задач
Практическая работа №6
«Создаем табличные модели» (задания 7 — 9)
 |  |
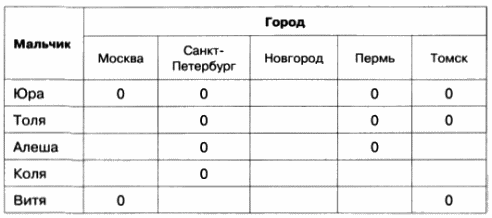
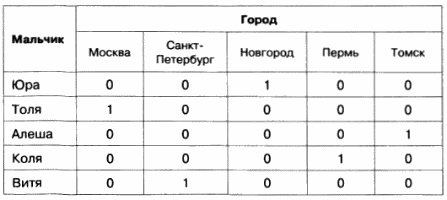
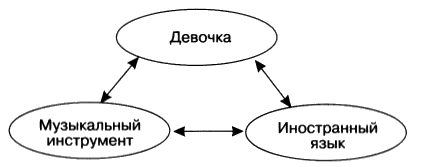
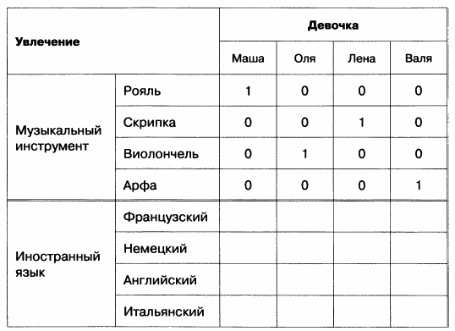
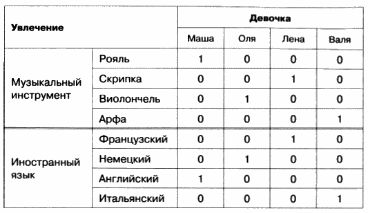
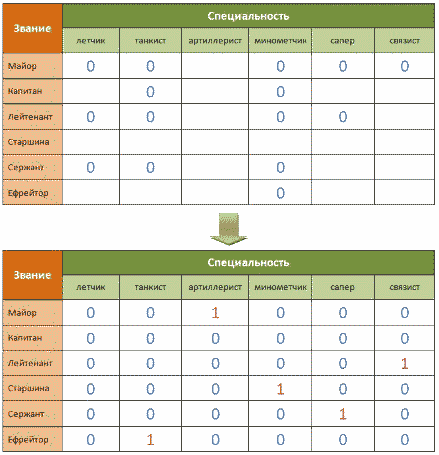
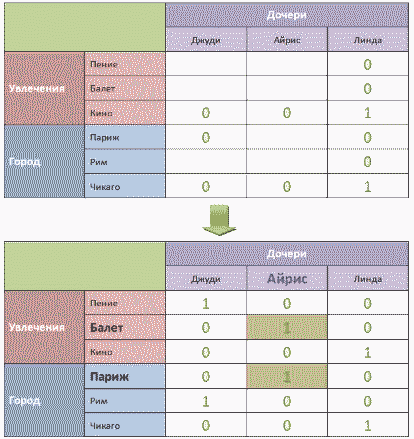
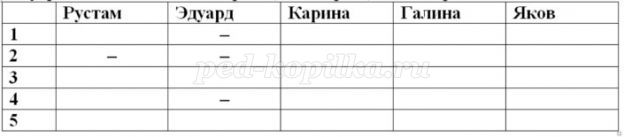
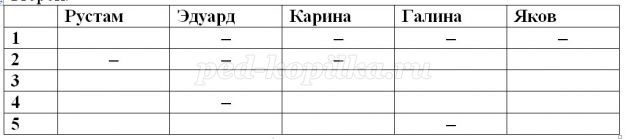
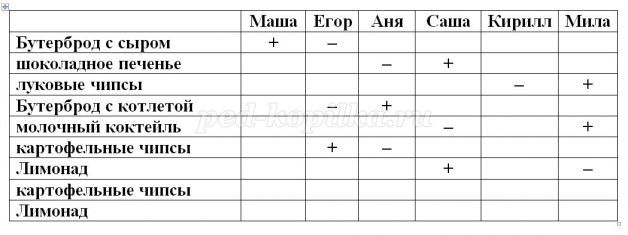
Табличное решение логических задачОбъекты двух классов могут находиться в отношении взаимно однозначного соответствия. В соответствующей таблице типа ООО в каждой строке и каждой графе будет находиться только одна 1, фиксирующая наличие связи между объектами. Это свойство можно использовать при решении логических задач. Пример 1Однажды в Артеке за круглым столом оказалось пятеро ребят родом из Москвы, Санкт- Петербурга, Новгорода, Перми и Томска: Юра, Толя, Алеша, Коля и Витя. Москвич сидел между томичем и Витей, петербуржец — между Юрой и Толей, а напротив него сидели пермяк и Алеша. Коля никогда не был в Санкт- Петербурге, а Юра не бывал в Москве и Томске, а томич с Толей регулярно переписываются. Нужно определить, в каком городе живет каждый из ребят. Анализ этого текста позволяет выделить два класса объектов: «мальчик» и «город». Нужно установить взаимно однозначное соответствие (выявить пары) между объектами этих классов. Наличие свойства у пары объектов «мальчик живет в городе» будем обозначать 1, а его отсутствие – 0 Отметим в таблице свойства пар, следующие из условия задачи: Таблица 2.15 После этого остается проследить, чтобы в каждой строке и каждой графе обязательно была одна и только одна 1: Таблица 2.16 Таким образом, Юра живет в Новгороде, Толя – в Москве, Алеша — в Томске, Коля — в Перми, Витя — в Санкт-Петербурге. Пример 2Маша, Оля, Лена и Валя — замечательные девочки. Каждая из них играет на каком-нибудь музыкальном инструменте и говорит на одном из иностранных языков. Инструменты и языки у них разные. Маша играет на рояле. Девочка, которая говорит по-французски, играет на скрипке. Оля играет на виолончели. Маша не знает итальянского языка, а Оля не владеет английским. Лена не играет на арфе, а виолончелистка не говорит по-итальянски. Нужно определить, на каком инструменте играет каждая из девочек и каким иностранным языком она владеет. В задаче рассматриваются объекты классов «девочка» (объекты с именами «Маша», «Оля», «Лена» и «Валя»), «музыкальный инструмент» («рояль», «скрипка», «виолончель», «арфа») и «иностранный язык» («французский», «немецкий», «английский», «итальянский»). Пары образуются из объектов классов «девочка» — «музыкальный инструмент», «девочка» — «иностранный язык», «музыкальный инструмент» — «иностранный язык», причем между объектами этих классов существует взаимно однозначное соответствие: В условии задачи явно указано наличие (отсутствие) связи между некоторыми объектами рассматриваемых классов. Можно построить две отдельные таблицы типа ООО для пар «девочка — музыкальный инструмент» и «девочка — иностранный язык». Более удобно соединить их в одну таблицу. Наличие свойства у пары объектов «девочка играет на музыкальном инструменте» («девочка владеет иностранным. языком») будем обозначать 1, а его отсутствие — 0. В рассматриваемом примере удобно вначале заполнить верхнюю часть таблицы на основании той информации, что между множеством девочек и множеством музыкальных инструментов существует взаимно однозначное соответствие, а также что: Таблица 2.17 Теперь, учитывая связи, зафиксированные в первой части таблицы, приступим к заполнению ее второй части: Таблица 2.18 Таким образом, увлечения Маши — рояль и английский, Оли — виолончель и немецкий, Лены — скрипка и французский, Вали — арфа и итальянский. Коротко о главномОбъекты двух классов находятся в отношении взаимно однозначного соответствия, если: В соответствующей таблице типа ООО в каждой строке и каждой графе будет находиться только одна 1, фиксирующая наличие связи между объектами. Это свойство можно использовать при решении логических задач. Вопросы и задания1. Приведите пример двух классов, объекты которых находятся в отношении взаимно однозначного соответствия. 2. В финале турнира Российской Армии по шахматам встретились представители шести воинских званий: майор, капитан, лейтенант, старшина, сержант и ефрейтор, причем разных специальностей: летчик, танкист, артиллерист, минометчик, сапер и связист. Определите специальность и звание каждого из шахматистов по следующим данным: Три дочери писательницы Дорис Кей — Джуди, Айрис и Линда — тоже очень талантливы. Они приобрели известность в разных видах искусств — пении, балете и кино. Все они живут в разных городах, поэтому Дорис часто звонит им в Париж, Рим и Чикаго. Известно, что: Где живет Айрис и какова ее профессия? Материал частично взят с сайта http://ikthelp.ru/ Практическая работа №6 |