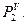Методы, используемые при нахождении линии пересечения поверхностей
Нами будут рассмотрены два метода, используемые при нахождении линии пресечения поверхностей:
· метод вспомогательных секущих плоскостей-«посредников»;
· метод вспомогательных концентрических сфер–«посредников».
Алгоритм решения каждым из методов будет рассмотрен на конкретном примере.
Возможны 3 случая расположения пересекающихся поверхностей относительно плоскостей проекций:
· пересекающиеся поверхности занимают проецирующее положение;
· одна из пересекающихся поверхностей занимает общее положение, вторая частное.
· обе поверхности общего положения.
Выбор посредников зависит от заданных поверхностей и их взаимного положения.
2.1. Метод вспомогательных секущих плоскостей-«посредников».
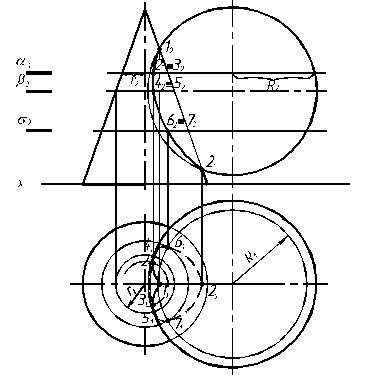
Пример. Построить линию пересечения поверхностей сферы и конуса (обе поверхности занимают общее положение).
Применяем общий алгоритм решения:
1. Определяем зону пересечения поверхностей.
2. Определяем характерные точки, принадлежащие линии пересечения:
опорные точки (наивысшая – точка 1 и наинизшая — точка 2 на очерковых образующих).
3. Определяем промежуточные точки. В качестве «посредников» выбираем плоскости частного положения (плоскости горизонтального уровня), которые пересекает сферу и конус по окружностям. Секущие плоскости проводим в зоне пересечения поверхностей.
4. Полученные точки соединяем плавной кривой. Точность аппроксимации линии пересечения зависит от принятого количества секущих плоскостей посредников.
5. Видимость полученной линии пересечения поверхностей решаем методом конкурирующих точек.
Примечание: если одна из поверхностей занимает проецирующее (частное) положение, то одна из проекций линии пересечения уже известна.
2.2. Метод вспомогательных концентрических сфер-«посредников»
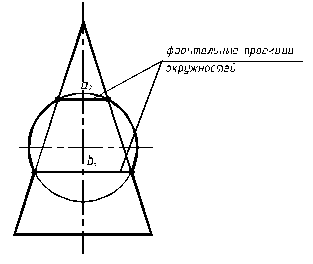
Сфера, если центр ее расположен на оси поверхности вращения, пересекает эту поверхность по окружностям a и b (рис. 9.3). Поэтому вспомогательные секущие сферы используют для построения линии пересечения поверхностей вращения.
Способ концентрических секущих сфер-«посредников» применяется в случае, если:
· пересекающиеся поверхности являются поверхностями вращения;
· оси вращения поверхностей пересекаются;
· оси вращения пересекающихся поверхностей параллельны одной из плоскостей проекций.
Пример. Построить линию пересечения поверхностей двух конусов (обе поверхности занимают общее положение).
При решении поставленной задачи выполняем пункты 1-3 общего алгоритма (область пересечения, характерные точки).
При поиске промежуточных точек используем в качестве поверхностей-«посредников» концентрические сферы. Центр, через который проводятся концентрические секущие сферы, является центром пересечения осей симметрии поверхностей. Предварительно находим максимальный и минимальный радиусы секущих сфер.
Rmin – радиус сферы от центра пересечения осей до наименее удаленной точки области пересечения поверхностей. Сфера минимального радиуса должна касаться одной поверхности и пересекать другую.
Rmax – радиус сферы от центра пересечения осей до наиболее удаленной точки области пересечения поверхностей.
Полученные точки соединяем плавной кривой. Точность аппроксимации линии пересечения поверхностей зависит от принятого количества вспомогательных концентрических сфер-«посредников». Определяем видимость полученной кривой.
Метод «Монжа» (частный случай)
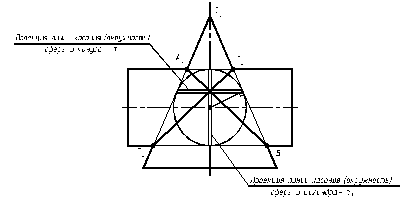
Теорема Монжа. Две поверхности вращения второго порядка, вписанные в третью поверхность вращения второго порядка или описанные вокруг неё, пересекаются между собой по двум плоским кривым второго порядка.
Теорему иллюстрирует рис. 9.5. В соответствии с этой теоремой линии пересечения конуса и цилиндра, описанных около сферы, будут плоскими кривыми – эллипсами, фронтальные проекции которых изображаются прямыми A2 B2 и C2 D2 , проходящие через точки пересечения очерков поверхностей вращения и точки пересечения окружностей m и n.
РАЗДЕЛ V. Тема: «Перспектива»
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Линия пересечения поверхностей
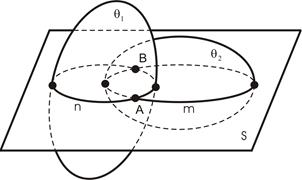
Линией пересечения поверхностей является линия, одновременно принадлежащая обеим пересекающимся поверхностям. Для построения точек линии пересечения используем метод вспомогательных секущих плоскостей.
Пусть даны две пересекающиеся поверхности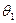 
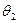
и 
(рис. 40).
1. Проводим вспомогательную секущую плоскость S так, чтобы она пересекала обе данные поверхности.
2. Находим линии n и m пересечения плоскости S с поверхностями 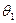и 
3. Определяем точки А и В взаимного пересечения линий n и m, лежащих в плоскости S.
Рис. 40. Пересечение поверхностей
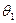
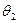
Точки А и В одновременно принадлежат поверхности и и, следовательно, являются точками искомой линии пересечения двух поверхностей. Проведя ряд вспомогательных секущих плоскостей, получим ряд точек, аналогичных точкам А и В. Линия, последовательно соединяющая эти точки, будет искомой линией пересечения двух поверхностей. Методом секущих плоскостей решаются задачи 4 и 6.
Дано: многогранник и поверхность вращения. С помощью вспомогательно-секущих плоскостей построить линию пересечения многогранной и поверхности вращения, выделив ее видимые и невидимые участки (пример на рис. 41, 42).
Указания к задаче 4
По табл. 4 определяется номер рисунка (см. приложение к табл. 4), на котором представлены две поверхности: одна – вращения, другая – многогранник (см. табл. 4). Количество граней n многогранника также указано в таблице, дано смещение Х от центра одной из поверхностей. Длину или высоту второй поверхности студент выбирает самостоятельно. Задачу решают в трех проекциях.
Намечают расположение вспомогательных секущих плоскостей частного положения (уровня) и с их помощью определяют характерные и промежуточные точки линии пересечения поверхностей. Плоскости следует выбирать так, чтобы линии их пересечения с поверхностями проецировались в простейшие фигуры (окружности или прямые).
| № вар. | Рисунок | n граней | х | № вар. | Рисунок | n граней | х |
| — | |||||||
| — | — | ||||||
| — | |||||||
| — | — | ||||||
| — | |||||||
| — | |||||||
| Продолжение таблицы 4 | |||||||
| — | — | ||||||
| — | |||||||
| — | |||||||
| — | — | ||||||
| — | — | ||||||
| — | — | ||||||
| — | |||||||
| — | — | ||||||
| — | |||||||
| — | — | ||||||
| — | |||||||
| — | |||||||
| — |
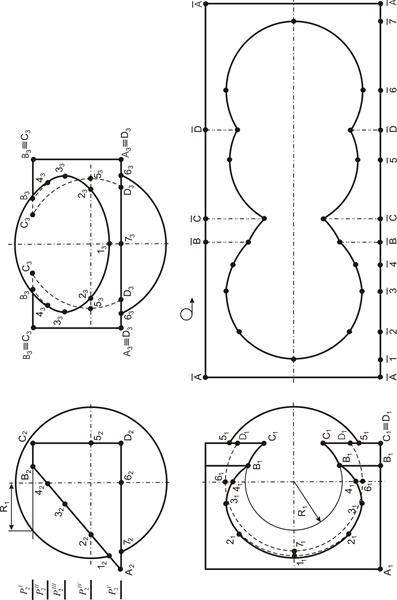
На примере решения задачи 4 (см. рис. 41) представлены сфера и проецирующая призма АВСD, следовательно, на фронтальной проекции линия пересечения уже определена. Вспомогательные плоскости в данном случае горизонтальные, они пересекают сферу по окружностям, а призму – по прямоугольникам. Точками пересечения поверхностей являются точки пересечения контуров фигур сечения поверхностей, лежащих в одной и той же вспомогательно-секущей плоскости. Каждая секущая плоскость может определить от одной до четырех точек линии пересечения в зависимости от характера пересекающихся поверхностей, их расположения относительно друг друга и положения секущей плоскости. Для гранной поверхности необходимо определить точки пересечения, принадлежащие ребрам, а для поверхности вращения – очерковым образующим.
На чертеже сфера представлена своим очерком на фронтальной и профильной проекции окружности главного меридиана, а на горизонтальной проекции – экватором.
Рис. 41. Сфера и призма
Точки 1 и 7 принадлежат главному меридиану на плоскости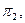 
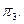
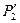
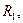
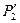
а точки 4 и 6 – на плоскости 
Точки 2 и 5 лежат на экваторе (21 и 51). Все остальные точки лежат на параллелях. По грани призмы ВС проводим первую горизонтальную плоскость 
– она пересекает сферу по окружности 
а призму – по грани ВС. На горизонтальной проекции определяют точки В1 и С1. Для нахождения остальных точек поступают так же, проводя плоскости до 
Построить развертку многогранной поверхности и нанести на ней линию пересечения (заданная поверхность задачи 4).
Указания к задаче 5
Определяют натуральную величину одного из ребер многогранника и строят одну грань, затем последовательно к ней пристраивают остальные грани. Линия пересечения поверхностей наносится на развертку с помощью характерных точек.
На рис. 41 представлена развертка прямой призмы, у которой натуральная величина ребра – горизонтальные проекции, натуральная величина основания – фронтальная проекция.
На рис. 42 представлено пересечение трехгранной пирамиды и цилиндра. При решении задачи используют горизонтальные плоскости, которые пересекают пирамиду по треугольникам, подобным основанию, а цилиндр – по прямоугольникам. На рис. 42 натуральная величина ребра у трехгранной пирамиды – это профильная прямая S3B3. Горизонтальная проекция основания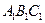 
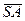
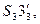
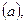
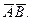
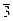
– это натуральная величина. По чертежу на ребре 
откладывается действительная величина 
проводится линия, параллельная основанию. На горизонтальной проекции пирамиды проводим дополнительную прямую через точку 31 до встречи с основанием 
и затем эту величину переносим на 
Точка пересечения двух прямых определяет положение точки 
на развертке.
Рис. 42. Пирамида и цилиндр
Даны две пересекающиеся поверхности вращения. Способом вспомогательно-секущих плоскостей построить линию их пересечения, выделив ее видимые и невидимые участки (пример решения задачи на рис. 43).
Указания к задаче 6
По табл. 5 определяется номер рисунка (см. приложение к табл. 5), на котором представлены две поверхности вращения и заданы координаты центра расположения осей одной из поверхностей. Чертежи выполняются по размерам, представленным в таблице, где d1 и d2 – диаметры пересекающихся поверхностей, h – высота одной из поверхностей (если высота или длина второй поверхности не указаны, студент принимает ее самостоятельно), X, Y, Z – смещения от центра одной из поверхностей.
| № вар. | № рис. | d1 | d2 | h | x | y | z | № вар. | № рис. | d1 | d2 | h | x | y | z |
| -15 | — | — | — | ||||||||||||
| — | — | -30 | — | ||||||||||||
| — | — | — | -10 | — | — | ||||||||||
| — | -30 | — | |||||||||||||
| — | — | — | -15 | — | |||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | — | — | — | |||||||||
| — | — | — | — | — | — | ||||||||||
| — | — | — | |||||||||||||
| — | — | — | — | -10 | — | ||||||||||
| -20 | — | -20 | — | — | |||||||||||
| Продолжение таблицы 5 | |||||||||||||||
| — | — | — | — | ||||||||||||
| — | — | — | — | — | — | ||||||||||
| — | -10 | — | — | — | — | — | |||||||||
| — | -10 | — | -20 | — | |||||||||||
| — | — | — | — | — | — | ||||||||||
| — | — | — | |||||||||||||
| — | — | — | — | ||||||||||||
| — | -10 | — | — | -20 | — | ||||||||||
| -25 | — | -25 | — | — | |||||||||||
| — | — | — | — | ||||||||||||
| — | — | ||||||||||||||
| — | — | — | |||||||||||||
| — | — | — | — | — | — | ||||||||||
| -15 | — | — | — | — |
На рис. 43 дан пример решения задачи 6 – пересечение поверхностей вращения (в нашем случае усеченный конус и цилиндр). Цилиндр на фронтальной плоскости проекций проецируется действительной величиной основания. Наиболее рациональный метод решения этой задачи – метод секущих плоскостей. На фронтальной проекции цилиндра выбираем характерные точки (точки, лежащие на очерковых образующих): А, С, Е принадлежат очерковым образующим конуса, а точки N, B, D и M – образующим цилиндра. Чтобы получить более точно линию пересечения поверхностей, выбираем случайные точки 1, 2, 3 и 4.
Для нахождения горизонтальных проекций этих точек применяют горизонтальные плоскости Р. Усеченный конус пересекается этими плоскостями по окружности радиусом, равным расстоянию от оси вращения до очерковой образующей, а цилиндр – по прямоугольникам. Соединив последовательно эти точки, получим плавную линию пересечения.
Источник
