Способ линейной засечки

В способе линейной засечки положение выносимой в натуру точки С (рис. 8) определяют в пересечении проектных рассто­яний S₁ и S ₂, отложенных от исходных точек А и В. Этот способ обычно применяют для разбивки осей строительных конструкций в случае, когда проектные расстояния не превышают длины мер­ного прибора.

Наиболее удобно разбивку производить при помощи двух руле­ток. От точки А по рулетке откладывают расстояние S₁, а от точки В по второй рулетке — S₂. Перемещая обе рулетки при совмещен­ных нулях с центрами пунктов А и В, на пересечении концов отрезков S₁ и S ₂ находят положение определяемой точки С.

Способ полярных координат

Способ полярных координат широко применяют при разбивке осей зданий, сооружений и конструкций с пунктов теодолитных или полигонометрических ходов, когда эти пункты расположены срав­нительно недалеко от выносимых в натуру точек.

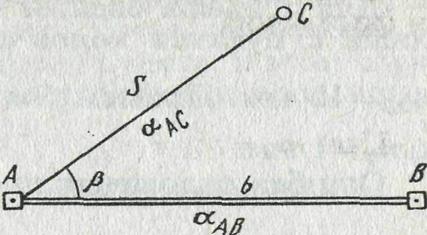
В этом способе положение определяемой точки С (рис. 10) находят на местности путем отложения от направления АВ проектного угла β и расстояния S. Проектный угол β находится как разность дирекционных углов а_АВ и α_AC, вычис­ленных как и расстояние S из реше­ния обратных задач по координатам точек А, В и С. Для контроля поло­жение зафиксированной точки С мо­жно проверить, измерив на пункте В угол β ׳ ’ и сравнив его со значением, полученным как разность дирекцион­ных углов а_BА и α_CA .

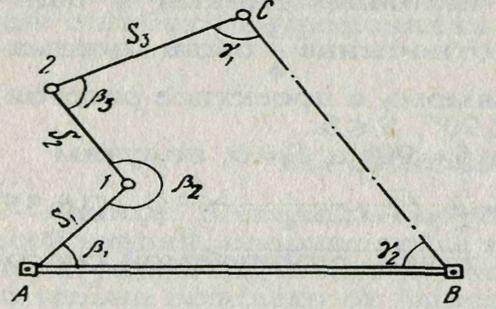
Если разбиваемая точка находится на значительном расстоянии от исходного пункта, то приходится несколько раз откладывать полярным способом проектные углы и расстояния, прокладывая проект­ный ход (рис. 11). При наличии пря­мой видимости с точки С на точку В для контроля измеряют примычные углы γ₁ и γ₂, образуя замкнутый уг­ловой полигон. Поэтому такой способ называют способом проектного поли­гона. При точных разбивочных рабо­тах углы полигона уравнивают, вычи­сляют по ним и проектным расстоя­ниям координаты точки С, сравнива­ют их с проектными и при необходи­мости редуцируют в проектное поло­жение.

Рис. 10. Схема разбивки спо­собом полярных координат

Рис. 11. Схема разбивки спосо­бом проектного полигона

При редкой разбивочной основе способ проектного полигона дожет быть использован для разбивки всех точек пересечения ос­новных осей сооружения от одного исходного пункта. В этом случае проектный ход с проектными углами и расстояниями прокладыва­ют полностью.

Источник

Способы геодезических разбивочных работ

Описание способов разбивочных работ

Выбор способа получения на местности планового положения точек зависит от вида геодезической сети на строительной площадке, особенностей местности и возводимого сооружения и других причин. Реализация того или иного способа заключается в основном в построении на местности заданных углов и расстояний. Для контроля положения вынесенной на местности точки ее координаты определяют другим независимым способом. Полевые разбивочные и контрольные работы выполняют по разбивочным чертежам , составленным по специальным расчетам, в которых исходными служат координаты опорных и проектных точек.

Способ прямоугольных координат

Этот способ обычно применяют в случаях, когда геодезической основой является строительная сетка ( рис. 1.46 ), ее вершины А, В, С, D закреплены на местности. Для выноса точки К (точка сооружения) по линии AD откладывай ют отрезок d 1 = У К — У А и по перпендикулярному AD направлению отрезок d 2 = Х к — Х А . Для построения отрезков и d 2 теодолит устанавливают над точкой А и приводят его в рабочее положение. Перекрестие нитей зрительной трубы наводят на точку D и от точки А в створе линии AD , фиксируемой теодолитом, откладывают горизонтальное проложение d 1 и получают точку Р. Теодолит переносят и устанавливают над точкой Р , приводят его в рабочее положение, откладывают прямой угол APР ‘. По направлению РР’ от точки Р откладывают горизонтальное проложение d 2, получают точку К , закрепляют ее.

Способ полярных координат

Этот способ широко применяется при разбивке зданий , сооружений и конструкций с пунктов полигонометрических и теодолитных ходов при малом расстоянии между исходными и выносимыми пунктами. Положение точки К на местности определяют путем откладывания от твердой линии АВ угла β и по полученному направлению АК горизонтального проложения d. Угол β = α А — α AK , где α А , α АК — дирекционные углы линий АВ и АК соответственно.

Способ прямой угловой засечки

В этом способе положение проектной точки К ( рис. 1.48 ) определяют путем откладывания в опорных точках А и В от опорной линии АВ проектных углов β 1 и β 2 . Базисом b является сторона разбивочной сетки или его измеренное значение. Проектные углы β 1 и β 2 вычисляют как разность дирекционных углов сторон, которые определяют из решения обратной геодезической задачи на плоскости по проектным координатам исходных пунктов и определяемой точки.

Способ обратной угловой засечки

На местности находят приближенное положение К’ выносимой проектной точки К ( рис. 1.49 ). Над точкой К’ устанавливают теодолит и с требуемой точностью измеряют углы β 1 , β 2 как минимум на три опорные точки с известными координатами. По формулам обратной угловой засечки вычисляют координаты точки К’ и сравнивают их с проектными значениями. По разности координат определяют величины редукций Δх, Δу или угловой Ө и линейный е элементы и смещают точку в проектное положение К .

Способ линейной засечки

В этом способе положение проектной точки К на местности определяют в пересечении проектных расстояний d 1 и d 2 , его применяют в основном для разбивки осей строительных конструкций при d 1 и d 2 меньше длины мерного прибора. Одной рулеткой от А откладывают d 1 , а рулеткой от точки В отрезок d 2 . Пересечение отрезков d 1 и d 2 (при совмещении нулей рулеток с точками А и В ) дает определяемую точку К ( рис. 1.51 ).

Способ пересечения створов

В этом способе положение точки К определяют при пересечении створов Т 1 Т’ 1 и Т 2 Т’ 2 . Створы на местности задают точками их пересечения с опорными сторонами. Положение точек T 1 , Т 2 определяют горизонтальными проложениями d 1 и d 2 от опорной точки В по опорным линиям ВА и ВС, а точек Т’ 1 , Т’ 2 — d’ 1 , d’ 2 от опорной точки Е по линиям EF и ED . Способ пересечения створов ( рис. 1.52 ) обычно используют для выноса в натуру труднодоступных точек, когда использование других методов затруднено.

Способ бокового нивелирования

Этот способ часто применяют для выноса осей при детальной разбивке и для установки строительных конструкций в проектное положение ( рис. 1.53 ). Пересечение К линии АВ с конструкцией определяют следующим образом. От точек А и В по перпендикуляру к АВ откладывают отрезки l и получают точки А’, В’ и линию А’В’ , параллельную АВ . Над точкой А’ устанавливают теодолит, приводят его в рабочее положение и перекрестие нитей наводят на точку В’ . К конструкции в горизонтальном положении устанавливают рейку и перемещают ее так, чтобы отсчет по ней был равен l . Пятка рейки даст положение точки К . Подобным образом определяют и положение точки К’.

Источник

Основы геодезии

О геодезии и разный полезный материал для геодезистов.

Линейная засечка

От пункта A с известными координатами XA, YA измерено расстояние S1 до определяемой точки P, а от пункта B с известными координатами XB, YB измерено расстояние S2 до точки P .

Графическое решение. Проведем вокруг пункта A окружность радиусом S1 (в масштабе чертежа), а вокруг пункта B – окружность радиусом S2; точка пересечения окружностей является искомой точкой; задача имеет два решения, так как две окружности пересекаются в двух точках (рис.2.9).

Исходные данные: XA, YA, XB, YB,

Измеряемые элементы: S1, S2,

Неизвестные элементы: X, Y.

Аналитическое решение. Рассмотрим два алгоритма аналитического решения, один – для ручного счета (по способу треугольника) и один – для машинного счета.

Алгоритм ручного счета состоит из следующих действий:

1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. вычисление в треугольнике ABP углов β1 и β2 по теореме косинусов:
(2.29)
3. вычисление угла засечки γ
(2.30)
4. вычисление дирекционных углов сторон AP и BP:

пункт P справа от линии AB
(2.31)

пункт P слева от линии АВ
(2.32)
5. решение прямых геодезических задач из пункта A на пункт P и из пункта B на пункт P:

1-е решение
(2.33)

2-е решение
(2.34)

Результаты обоих решений должны совпадать.

Алгоритм машинного решения линейной засечки состоит из следующих действий:

1. решение обратной геодезической задачи между пунктами A и B и получение дирекционного угла αAB и длины b линии AB,
2. введение местной системы координат X’O’Y’ с началом в точке A и осью O’X’, направленной вдоль линии AB, и пересчет координат пунктов A и B из системы XOY в систему X’O’Y’:
(2.35)
3. запись уравнений окружностей в системе X’O’Y’:
(2.36)

и совместное решение этих уравнений, которое предусматривает раскрытие скобок во втором уравнении и вычитание второго уравнения из первого:
(2.37)

откуда
(2.38)

Если искомая точка находится слева от линии AB, то в формуле (2.39) берется знак “-“, если справа, то “+”.
4. пересчет координат X’ и Y’ точки P из системы X’O’Y’ в систему XOY по формулам (2.2):
(2.40)

Источник

2.1.6.4. Способ линейной засечки

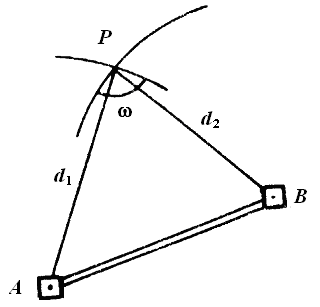
Способ линейной засечки может быть использован, если расстояние от выносимой точки до пунктов разбивочной сети меньше длины мерного прибора. Положение на местности искомой точки Р получают на пересечении двух дуг, радиусы которых равны проектным расстояниям идо пунктовАиВразбивочной сети (рис. 2.23).

Рис. 2.23. Построение точки способом линейной засечки

Точность построения точки Р способом линейной засечки может быть вычислена по формуле

, (2.29)

где – угол засечки;и– средние квадратические погрешности отложения расстояний.

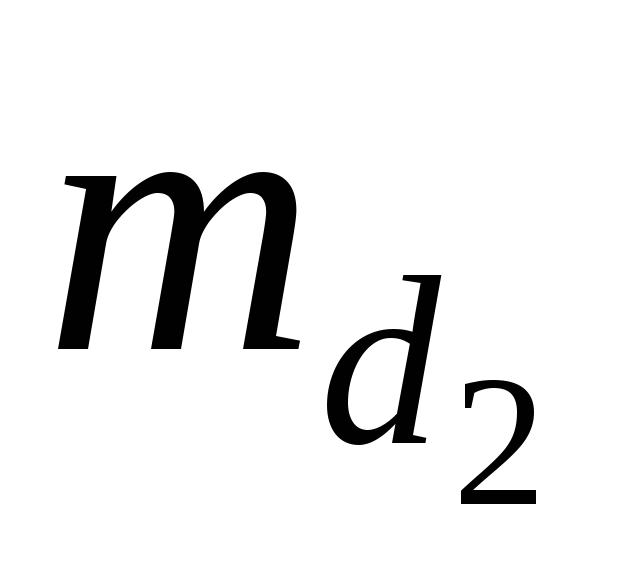
2.1.6.5. Способ проектного полигона

Способ проектного полигона применяют для выноса в натуру нескольких точек, если расстояния между ними не слишком велики. Из решения обратной геодезической задачи находят длины сторон , ии внутренние углы проектного полигона,,и (рис. 2.24). Затем, откладывая углы и расстояния, последовательно находят положения точекВ, C иD, которые вследствие погрешностей построения углов и расстояний не совпадут с проектными точками.

Рис. 2.24. Построение точек способом проектного полигона

В конечной точке D измеряют величину и магнитный азимут направления линейной невязкиDD. Если невязка не превышает допустимого значения, то точки В, С иD с помощью линейки перемещают в проектное положение по направлению магнитного азимутаDDна расстояния, пропорциональные их удалению от начала хода:

,.

Полученные точки закрепляют.

Основные элементы высотных разбивочных работ

2.1.7.1. Вынос точек с проектными отметками

Для выноса точек с проектными отметками используют методы геометрического, тригонометрического и гидростатического нивелирования.Метод геометрического нивелирования, обладающий высокой точностью и простотой реализации, имеет наибольшее распространение при строительстве. Метод тригонометрического нивелирования характеризуется меньшей точностью, однако этим методом можно значительно быстрее передавать отметки на монтажные горизонты. Гидростатическое нивелирование в строительстве используется обычно при выносе отметок под монтаж оборудования, когда превышения малы и предъявляются высокие требования к точности высотной разбивки.

Построение точек с проектными отметками методом геометрическогонивелирования производят двумя способами: выведением и редуцированием.

Пусть требуется вынести на местность точку В с проектной отметкой Н_В (рис. 2.25). Для выполнения этой задачи способом выведения посередине между точкой В и репером А с отметкой Н_A устанавливают нивелир. Производят отсчет а по рейке на репере и находят горизонт инструмента (визирования) Н_ГВ = H_А + а. Вычисляют отсчет b по рейке на точке В, при котором пятка рейки будет на проектном уровне b = H_ГВ – H_B. Затем рейку устанавливают в точке В так, чтобы отсчет по ней был равен вычисленному значению b. На коле, забитом предварительно в точке B, под пяткой рейки карандашом фиксируют высотное положение искомой точки.

При монтаже конструктивных элементов и установке оборудования применяют способ редуцирования. В этом случае нивелированием из середины находят фактическое превышение точки В над репероми сравнивают его с проектным превышением. В точкеB укладывают подкладку толщиной, верх подкладки будет на заданной проектной отметке.

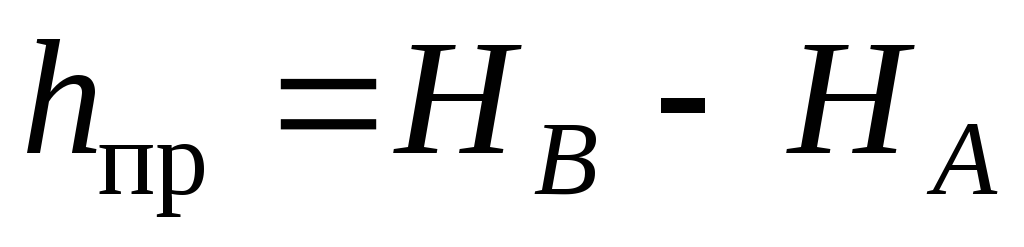
Рис. 2.25. Построение превышения методом геометрического нивелирования

Погрешность построения точек с проектными отметками методом геометрического нивелирования зависит от дальности визирования, точности нивелира и делений рейки, способа отсчитывания и других факторов. Экспериментальными исследованиями установлено, что погрешность измерения превышения составляет, мм:

= 0,02 + 0,002s– для прецизионного нивелира типа Н-05;

= 0,1 + 0,01s– для точного нивелира типа Ni-B3;

= 0,8 + 0,02s– для точного нивелира типа Н-3.

Расстояние sот нивелира до рейки в формулы подставляют в метрах. Оптимальная длина визирного луча составляет 25 м.

Точность способа выведения зависит от способа фиксации высоты разбиваемой точки: при забивании колышка до проектного уровня погрешность фиксации 2–4 мм, при прочерчивании по метке (пятке) рейки – 1 мм, при вывинчивании болта с резьбой – 0,1–0,5 мм.

При тригонометрическом нивелировании превышения вычисляют по измеренному расстоянию и углу наклона:

, (2.30)

где sиd– наклонное расстояние и соответствующее ему горизонтальное приложение;– угол наклона;I, –высота прибора и визирной цели;f– суммарная поправка за кривизну Земли и рефракцию.

Наклонные расстояния обычно измеряют светодальномером, а горизонтальные проложения получают из измерений мерными приборами. Угол наклона измеряют со средней квадратической погрешностью 2–3(теодолитом типа Т2) и 5« (теодолитом типа Т5К).

При использовании метода тригонометрического нивелирования необходимо с высокой точностью знать высоту теодолита I над пунктом разбивочной сети. Высота прибора может непосредственно измеряться с использованием рулетки или определяться косвенным путем с помощью нивелира и рейки.

При косвенном способе на расстоянии 2–3 м от пункта А разбивочной сети (рис. 2.26), на котором будет установлен теодолит, забивают кол или выбирают стабильную точкуK. При помощи нивелира и рейки измеряют превышениеh между пунктомАи точкойK. Затем над пунктомАустанавливают теодолит, приводят трубу в горизонтальное положение (отсчет по вертикальному кругу равен месту нуля М0) и делают отсчетb по рейке, установленной на точкеK. Тогда высотуI теодолита можно получить из выражения

. (2.31)

Рис. 2.26. Косвенный способ определения высоты теодолита

Погрешность определения высоты косвенным способом составляет 0,3–0,5 мм.

Гидростатическое нивелирование обеспечивает построение превышений с погрешностью 0,01–0,05 мм (с помощью прецизионного нивелира) и 1–2 мм (с помощью технического нивелира). В первом случае диапазон измеряемых превышений составляет всего 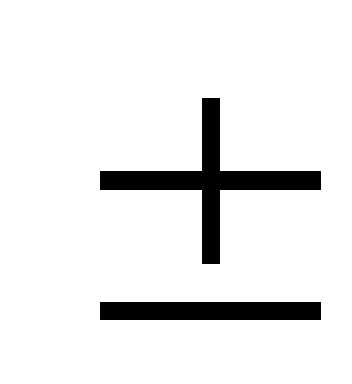25 мм.

В процессе гидростатического нивелирования следует избегать размещения приборов и шланга вблизи источников тепла и вентиляционных каналов, прямого попадания солнечных лучей, а также следует располагать шланги на уровне измерительных головок.

Источник