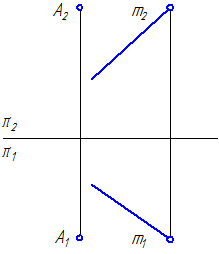Лекция способы преобразования проекций

Лекция 4. Способы преобразования ортогонального чертежа

4.1. Способ перемены плоскостей проекций

Чаще всего геометрические объекты расположены относительно плоскостей проекций в общем положении, и при решении задач для достижения поставленной цели необходимо выполнять много построений.

Количество построений можно значительно сократить, если геометрические элементы будут расположены в частном положении относительно плоскостей проекций.

Существуют два основных способа преобразования чертежа, при которых:

1. Объект остаётся неподвижным, при этом меняется аппарат проецирования;
2. Условия проецирования не меняются, но изменяется положение объекта в пространстве.

К первому способу относится способ перемены плоскостей проекций.

Ко второму – способ вращения (вращение вокруг линии уровня и вращение вокруг проецирующей прямой); способ плоскопараллельного перемещения.

Рассмотрим наиболее часто используемые способы при решении задач.

Способ перемены плоскостей проекций или способ введения дополнительных плоскостей проекций (ДПП) позволяет перейти от заданной системы плоскостей проекций к новой системе, более удобной для решения той или иной задачи.

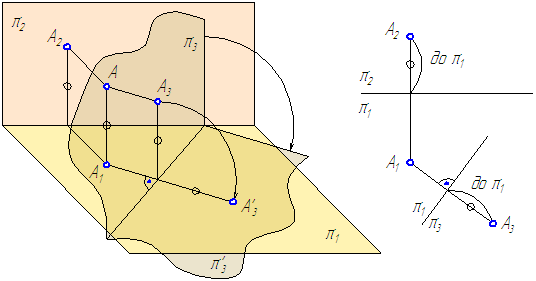
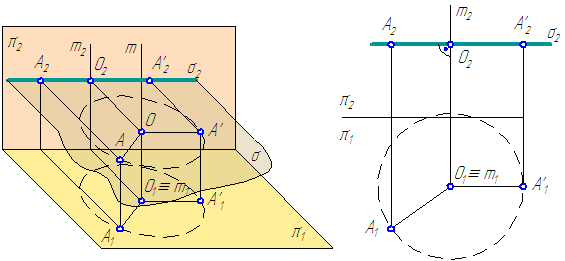
Рассмотрим положение точки А относительно известной системы плоскостей проекций π₂⊥π₁ (Рисунок 4.1, а и б).

Введём π₄⊥π₁, при этом получим новую систему двух взаимно перпендикулярных плоскостей. Положение точки А на эпюре будет в этом случае задано проекциями А₁ и А₄.

Правила перемены плоскостей проекций:

1. Новая плоскость проекций вводится перпендикулярно, по крайней мере, одной из заданных на чертеже плоскостей проекций;
2. ДПП располагается относительно проецируемого объекта в частном положении, удобном для решения поставленной задачи;
3. Новую плоскость совмещаем вращением вокруг новой оси проекций с плоскостью, которой она перпендикулярна на свободное место так, чтобы проекции не накладывались друг на друга.

а б

Рисунок 4.1 – Способ перемены плоскостей проекций

1. На чертеже новая проекция геометрического элемента находится на линии связи, перпендикулярной новой оси проекций:

1. Расстояние от А₄ до π₁/π₄ равно расстоянию от А₂ до π₂/π₁, так как величина этих отрезков (отмечены ○) определяет расстояние от точки А до плоскости проекций π₁.

При решении задачи необходимо заранее обдумать, как расположить новую плоскость проекций относительно заданных геометрических объектов (прямой, плоскости и др.), и как на чертеже провести новую ось проекций, чтобы в новой системе плоскостей заданные объекты заняли бы частные положения по отношению к новой плоскости проекций.

Упражнение

1. Спроецировать отрезок общего положения АВ в точку.

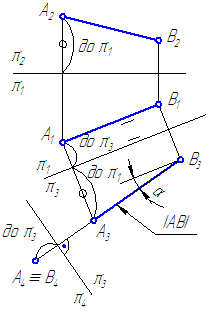
1. Введём ДПП π₄//А₁В₁ и π₄⊥π₁ (Рисунок 4.2). В новой системе двух взаимно перпендикулярных плоскостей проекций π₁/π₄ отрезок АВспроецируется на π₄ в натуральную величину и по этой проекции можем определить угол наклона отрезка к плоскости проекций π₁

Упражнение

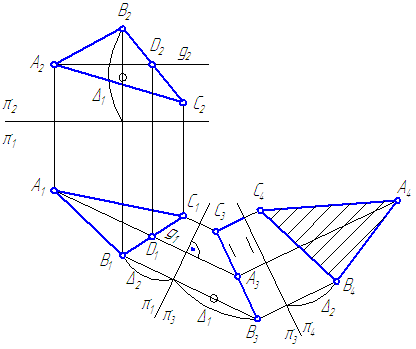
2. Дана плоскость общего положения – σ, заданная треугольником АВС (Рисунок 4.3).

Определить истинную величину треугольника.

1. Введём ДПП π₄⊥σ и π₄⊥π₁, для чего построим горизонталь в плоскости треугольника и проведём новую ось проекций π₁/π₄⊥g₁согласно теореме о перпендикуляре к плоскости. На π₄ плоскость σ спроецируется в прямую, что означает σ⊥πp₄.
2. Введём ДПП π₅//σ (π₄/π₅//А₄В₄С₄) и π₄⊥π₅. На π₅ проекция А₅В₅С₅ – есть истинная величина треугольника.

4.2. Способ вращения

Сущность способа вращения состоит в том, что положение системы плоскостей проекций считается неизменным в пространстве, а положение проецируемого объекта относительно неподвижных плоскостей изменяется.

Из сравнения сущности обоих способов видно, что решение задач, которые требуют применения преобразования ортогонального чертежа, может быть выполнено любым из этих способов, результат при этом должен получиться одинаковым. Основа выбора того или иного способа – рациональность решения.

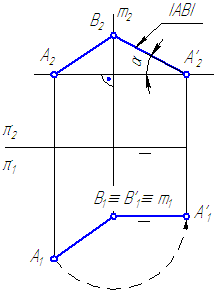
Вращение заданных элементов будем осуществлять вокруг проецирующей прямой, то есть прямой, перпендикулярной какой-либо плоскости проекций, при этом все точки заданных элементов поворачиваются в одну и ту же сторону на один и тот же угол (Рисунок 4.4, а и б). Ось вращения и объект вращения составляют твёрдое тело.

А – точка в пространстве;

О – центр вращения точки А;

АО – радиус вращения

а б

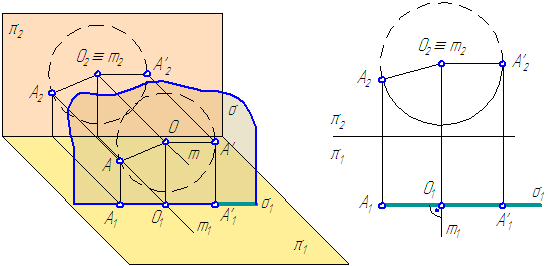
Рисунок 4.4 – Способ вращения вокруг прямой, перпендикулярной π₂

Точка описывает в пространстве окружность радиусом АО. Плоскость окружности перпендикулярна оси вращения (σ⊥m).

Так как m⊥π₂ , то σ//π₂, следовательно, σ⊥π₁, ⇒ σ₁⊥m₁, и поэтому σ проецируется на π₁ в виде прямой, перпендикулярной проекции оси вращения, а на π₂ траектория вращающейся точки проецируется в виде окружности с центром О₂≡m₂.

Пусть ось вращения m⊥π₁ (Рисунок 4.5, а и б). Плоскость окружности σ⊥m.

а б
Рисунок 4.5 – Вращение вокруг прямой, перпендикулярной π₁
\left.\begin\sigma\parallel\pi_1\\\sigma\perp \pi_2\\\end\right\> npu\;m\perp\pi_1\Longrightarrow\sigma_2\perp m_2
Свойства проекций

1. На плоскость проекций, перпендикулярную оси вращения, траектория вращающейся вокруг этой оси точки проецируется без искажения, то есть в окружность с центром, совпадающим с проекцией оси вращения на эту плоскость и радиусом, равным расстоянию от вращаемой точки до оси вращения.
2. На плоскость проекций, параллельную оси вращения, траектория вращающейся точки проецируется в отрезок, перпендикулярный проекции оси вращения на эту плоскость.
3. На плоскость проекций, перпендикулярную оси вращения, проекция вращаемого объекта своих размеров и формы не меняет.

Упражнение

Дано : отрезок общего положения – АВ.

Определить : способом вращения истинную величину отрезка и углы наклона его к плоскостям проекций.

1. Выберем ось вращения m⊥π₁ и проходящую через точку В (Рисунок 4.6).

На плоскости проекций π₂ проекция траектории перемещения точки А – прямая,

A_2 \overline\perp m_2\;u\;A_2\overline\parallel\pi_2/\pi_1

На плоскости проекций π₁ проекция траектории перемещения точки А – окружность радиусом |А₁В₁|.

Повернем отрезок до положения, параллельного плоскости проекций π₂. Получим натуральную величину отрезка.

Угол наклона отрезка АВ к плоскости проекций π₁ будет угол
\alpha=\angle\widehat_2> .

Для того, чтобы определить угол наклона АВ к плоскости проекций π₂, надо ввести новую ось вращения перпендикулярно π₂ и повторить построения.

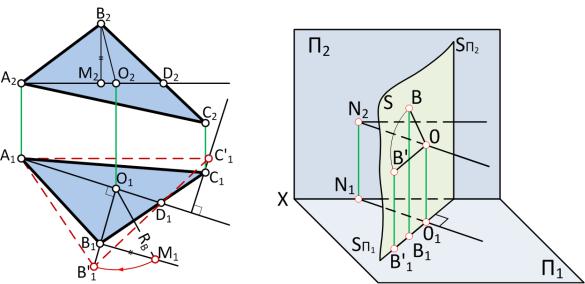
4.3. Определение истинной величины треугольника способом вращения

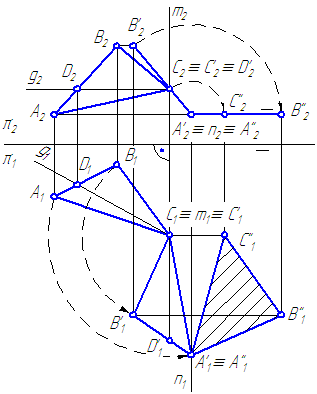
Пусть плоскость σ задана треугольником. Необходимо определить истинную величину треугольника (Рисунок 4.7).

Одним поворотом вокруг оси, перпендикулярной к плоскости проекций, истинную форму треугольника получить нельзя (так же как и введением одной ДПП).

Вращая вокруг оси m, перпендикулярной π₁ можно расположить плоскость ΔАВС⊥π₂ (а вращая вокруг оси n⊥π₂ можно расположить плоскость ΔАВС⊥π₁).

Рисунок 4.7

1. Положим σ’ должна быть перпендикулярна π₂. Для чего построим CD – горизонталь h плоскости σ. Введём первую ось вращения m⊥π₁, например, через точку С.
2. Повернём треугольник вокруг m до положения, когда
   \overline\perp\pi_2\Rightarrow\overline_1\overline_1\perp\pi_2/\pi_1
   На основании 3-го свойства, новая горизонтальная проекция треугольника \overline по величине должна равняться A₁B₁C₁, а фронтальная проекция треугольника будет представлять отрезок.
3. Введём вторую ось вращения n⊥π₂ через точку \overline_2 . Повернём фронтальную проекцию \overline в новое положение \overline<\overline\overline\overline>\parallel\pi_2/\pi_1 . На π₁ получим треугольник \overline<\overline\overline\overline> , равный истинной величине треугольника АВС.

4.4. Задачи для самостоятельной работы

Двумя способами преобразования ортогонального чертежа:

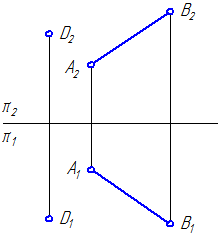
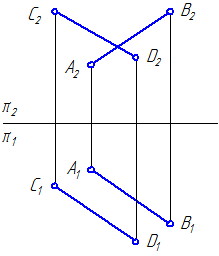
1. Определить расстояние от точки D до отрезка АВ – общего положения (Рисунок 4.8).

Рисунок 4.8

2. Определить расстояние между двумя параллельными прямыми общего положения (АВ//CD) (Рисунок 4.9).

Рисунок 4.9

3. Определить расстояние между двумя скрещивающимися прямыми, заданными отрезками АВ и CD (Рисунок 4.10).

Рисунок 4.10

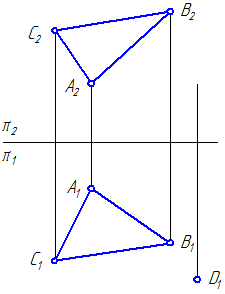
4. Построить недостающую проекцию точки D при условии, что задана σ=ΔАВС – общего положения и первая проекция точки D₁, Dотстоит от плоскости σ на 30 мм (Рисунок 4.11).

Рисунок 4.11

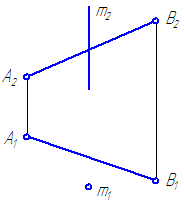
5. Дан отрезок АВ – общего положения. Ось вращения не проходит через АВ (Рисунок 4.12). Определить способом вращения истинную величину АВ.

Рисунок 4.12

6. Задана прямая общего положения m и точка А вне прямой. Построить плоскость, проходящую через точку А и перпендикулярную прямой m (Рисунок 4.13).

Рисунок 4.13

Источник

08-10-2014_23-25-49 / ЛЕКЦИЯ 4 Способы преобразования проекций

Лекция 4. Способы преобразования проекций

1. Способ замены плоскостей проекций.

2. Способы вращения (вращение вокруг оси, перпендикулярной к плоскости проекций; способ плоскопараллельного перемещения; вращение вокруг оси, параллельной плоскости проекций; способ совмещения).

Задание прямых линий и плоских фигур в частных положениях относительно плоскостей проекций значительно упрощает решение задач, а подчас позволяет получить ответ или непосредственно по чертежу, или при помощи простейших построений.

Способы преобразования чертежа дают возможность переходить от общих положений прямых линий и плоских фигур относительно плоскостей проекций к частным. Это достигается:

1) изменением положения прямой линии или плоской фигуры путем их вращения вокруг некоторой оси так , чтобы прямая или фигура оказались в частном положении относительно неизменной системы плоскостей проекций (способ вращения и частный случай его — способ совмещения);

2) заменой системы плоскостей проекций новой системой так,

чтобы прямая линия или плоская фигура, не изменяя своего положения в пространстве, оказались в каком-либо частном положении в новой системе плоскостей проекций (способ замены плоскостей проекций).

1 Способ замены плоскостей проекций

Способ замены плоскостей проекций широко применяют в машиностроении.

Сущность способа: положение точек, плоских фигур, поверхностей в пространстве не изменяется, а система плоскостей проекций π 2 /π 1 дополняется новыми плоскостями, образующими с π 1 , π 2 или между собой системы двух взаимно перпендикулярных плоскостей, принимаемых за плоскости проекций.

Каждая новая система выбирается так, чтобы по отношению к заданным геометрическим элементам она заняла положение, наиболее удобное для выполнения требуемого построения.

На рис. 45 изображена точка А в системе π 2 /π 1 . Затем плоскость π 2 заменена плоскостью проекций π 4 , которая также перпендикулярна к π 1 . Образовалась система π 4 /π 1 ; x 1 — ось проекций в новой системе плоскостей.

Горизонтальная проекция точки А своего положения не меняет. Проекция A 4 точки А на плоскости π 4 находится от плоскости π 1 на том же расстоянии, что и проекция A 2 на плоскости π 2 , что позволяет легко построить проекцию точки А на плоскости π 4 .

Для перехода от пространственного изображения к чертежу надо плоскость π 4 вращением около новой оси проекции x 1 совместить с плоскостью π 1 .

Построение проекции A 4 на эпюре (рис. 46) производится в следующем порядке:

а) из горизонтальной проекции A 1 точки А опускается перпендикуляр на новую ось проекций x 1 ;

б) на этом перпендикуляре от точки A x 1 откладывается отрезок A x 1 A 4 , равный расстоянию старой фрон-

тальной проекции A 2

плоскостью π 4 , перпендикулярной π 2 осуществляется аналогично.

Построение проекции В 4 на эпюре (рис. 47) производится в следующем порядке:

а) из фронтальной проекции В 2 точки В опускается перпендикуляр на новую ось проекций x 1 ;

б) на этом перпендикуляре от точки В x 1 откладывается отрезок В x 1 В 4 , равный расстоянию В 1 В Х.

Задача 1. Определить истинную величину отрезка АВ (рис. 48)

В заданной системе плоскостей проекций отрезок занимает общее положение. Заменим плоскость проекций π 2 новой плоскостью π 4 , параллельной заданному отрезку АВ. Новая ось проекций x 1 при этом, очевидно, должна быть параллельна горизонтальной проекции A 1 B 1 отрезка.

Для нахождения новой фронтальной проекции отрезка построены новые фронтальные проекции его концов (точек А и В ) в системе π 2 / π 4 . Новая фронтальная проекций A 4 B 4 отрезка — истинная величина отрезка АВ .

На рис. 49 эта же задача решена путем замены плоскости проекций π 1 новой плоскостью π 4 . В этом случае новая ось должна быть расположена параллельно A 2 B 2 . Новая горизонтальная проекция ( A 4 B 4 ) отрезка — его истинная величина.

Задача 2. Определить расстояние от точки S до плоскости треугольника ABC.

Расстояние от точки до плоскости может быть определено непосредственно на эпюре, если плоскость будет проецирующей.

Заменим плоскость π 2 на новую плоскость проекций π 4 (рис.50) . Плоскость π 4 выберем так, чтобы она оказалась перпендикулярной плоскости треугольника ABC . Новая ось проекции x 1 при этом должна быть перпендикулярна горизонтальной проекции горизонтали. Проецируем треугольник АВС и точку S на новую плоскость. Через точку S 4 проводим перпендикуляр к отрезку A 4 C 4 . Искомое расстояние S 4 K 4.

Задача 3. Определить угол наклона плоскости Р к горизонтальной плоскости проекций (рис. 51)

Если плоскость, заданная следами, фронтально-проецирующая, то угол, образованный фронтальным следом с осью проекций, и будет определять угол наклона плоскости к горизонтальной плоскости проекций.

Заменим систему плоскостей π 2 / π 1 новой системой π 4 /π 1 . Новую ось x 1 проведем перпендикулярно

следу Pπ 1 . Положение следа Pπ 1 не изменяется. Точка Рх 1 — точка схода следов в новой системе.

ного следа Pπ 4 плоскости, берем

N и находим ее новую

фронтальную проекцию N 4 .

Через точки Рх 1 и N 4

новый фронтальный след Pπ 4

Найденный угол α и будет

Задача 4. Определить натуральную фигуру треугольника ABC

Треугольник спроецируется в натуральную величину на какую-либо плоскость проекций, если он окажется параллельным этой плоскости .

Для того чтобы треугольник ABC оказался параллельным одной из плоскостей проекций, необходимо выполнить двойную замену плоскостей (рис.

ним на плоскость π 4 .

кость π 4 выберем перпен-

горизонтальной проекции горизонтали. На новую фронтальную плоскость проекций треугольник спроецируется в виде прямой линии C 4 A 4 B 4 . Затем введем новую плоскость проекций π 5 параллельно плоскости треугольника.

Горизонтальная проекция A 5 B 5 C 5 треугольника ABC в новой системе

— натуральная величина треугольника ABC .

2 Способы вращения

При вращении точки вокруг неподвижной оси (оси вращения), точка описывает окружность, расположенную в плоскости, перпендикулярной оси вращения. В качестве оси вращения обычно используются прямые, перпендикулярные плоскости проекций или прямые параллельные плоскостям проекций.

2.1 Вращение вокруг оси, перпендикулярной к плоскости проекций

На рис. 53 показано вращение точки А относительно оси Z , перпендикулярной к плоскости π 1 . При вращении вокруг оси Z точка А будет перемещаться по окружности, лежащей в плоскости, перпендикулярной оси вращения (параллельной плоскости проекций π 1 ). Если точку А переместить из положения А в положение A т. е. повернуть ее вокруг оси Z на некоторый угол α, то ее горизонтальная проекция ( A 1 ) займет положение A 1 , описав при этом дугу радиуcа ZA , а фронтальная проекция (A 2 ) точки переместится по прямой A 2 A 2 , параллельной оси Х. Если ось вращения Z (рис. 54) перпендикулярна к плоскости проекций π 2 , то при вращении точки В вокруг этой оси фронтальная проекция траектории ее перемещения будет окружностью, а горизонтальная — прямой, параллельной оси Х .

Задача 1. Определить натуральную величину отрезка АВ прямой l (рис.55)

Проводим ось вращения i ( i 1, i 2 ) перпендикулярно π 1 через точку В ( B 1 B 2 ) прямой l ( l 1, l 2 ). При вращении прямой l вокруг оси i точка В прямой останется неподвижной, так как принадлежит оси,

а точка А будет вращаться по правилам, рассмотренным выше. Точку А поворачиваем относительно оси i на угол α, прямая l в этом случае займет положение, параллельное плоскости π 2 ,

а следовательно, спроецируется на эту плоскость в натуральную величину

( A 2 B 2 ). Одновременно в натуральную

величину проецируется угол наклона

( ) отрезка АВ к плоскости π 1 .

общего положения в

проецирующее положение (рис. 56)

Две плоскости взаимно перпендикулярны, если одна из них проходит через прямую, перпендикулярную к другой плоскости. Следовательно, если какую-либо прямую, принадлежащую плоскости, преобразовать в проецирующую, то плоскость тоже станет проецирующей. Проще всего для этой цели воспользоваться линиями уровня. Если плоскость (АВС) вращать вокруг оси i ,

может быть повернута в положение, перпендикулярное плоскости π 2 , при этом плоскость становится фронтально проецирующей. Для упрощения построений на комплексном чертеже горизонталь АК и ось вращения i проведены через вершину А треугольника АВС. Для построения новой горизонтальной проекции A 1 B 1 ‘ C 1 ‘ треугольника АВС можно воспользоваться одним из следующих соображений:

1) так как угол наклона плоскости треугольника АВС к плоскости π 1 при вращении вокруг оси i π 1 не изменяется, то A 1 B 1 ‘ C 1 ‘ = A 1 B 1 C 1 ;

2) величина угла поворота точек B 1 и C 1 равна величине угла поворота горизонтальной проекции горизонтали ( = K 1 A 1 K 1 ‘). Точка A 1 неподвижна, так как она принадлежит оси вращения. Остальные построения основаны на правилах, изложенных ранее, и понятны из

АВ’С’ перпендикулярен π 2

фронтальная проекция B 2 ‘ A 2 C 2 ‘ вырождается в прямую линию.

плоскость преобразовать в

проецирующую, ее необходимо вращать вокруг оси i π 2 , а в качестве вспомогательной линии уровня взять фронталь.

2.2 Способ вращения без указания положения осей (плоскопараллельное перемещение)

При вращении любой пространственной формы около оси, перпендикулярной одной из плоскостей проекций, проекция ее на эту плоскость но своей величине не изменится. Изменится лишь положение этой проекции относительно оси проекций. Что касается другой проекции — на плоскость, параллельную оси вращения, — то все точки этой проекции (за исключением точек, расположенных на оси вращения) перемещаются по прямым, параллельным оси проекций. Пользуясь этим, для решения той или иной задачи можно применять способ вращения, не изображая на чертеже осей вращения. На рис. 57 определена истинная величина треугольника ABC способом вращения без указания положения осей. Сначала вращением вокруг некоторой оси, перпендикулярной плоскости π 1 (положение ее на чертеже не указано), треугольник поставлен перпендикулярно плоскости π 2 , затем поворотом вокруг какой-либо оси, перпендикулярной плоскости π 2 , треугольник приведен в положение, параллельное горизонтальной плоскости проекций π 1 .

2.3 Вращение вокруг оси, параллельной плоскости проекций

Вращение вокруг линии, параллельной плоскости проекций, позволяет повернуть плоскую фигуру в положение, параллельное плоскости проекций. В этом случае ортогональная проекция фигуры будет конгруэнтна оригиналу, что позволит определить все метрические характеристики проецируемой фигуры непосредственно по ее проекции без каких-либо дополнительных построений.

На рис. 58 показано вращение треугольника вокруг горизонтали АD . Точка А , расположенная на оси вращения, останется на месте. Следовательно, для нового изображения горизонтальной проекции треугольника надо найти положение других двух его вершин.

Рассмотрим вращение вершины В (рис. 59). Точка В вращается вокруг некоторой горизонтально расположенной оси ОN , описывая дугу окружности, лежащую в плоскости S . Эта плоскость перпендикулярна к оси вращения и, следовательно, является горизонтально-проецирующей; поэтому горизонтальная проекция окружности, описываемой точкой В , должна находиться на следе Sπ 1 .

Если треугольник, одной из вершин которого является точка В , займет положение, параллельное плоскости π 1 , то радиус вращения точки В (отрезок ОВ ) расположится параллельно плоскости π 1 и ОВ = O 1 B 1 . Опуская перпендикуляр из точки B 1 на A 1 D 1 находим горизонтальную проекцию центра вращения – точку O 1 и горизонтальную проекцию радиуса вращения точки В (отрезок O 1 B 1 ), а затем находим фронтальную проекцию радиуса вращения – O 2 B 2 . Методом прямоугольного треугольника определяем натуральную величину радиуса вращения точки В : по катетам O 1 B 1 и B 1 M 1 строим прямоугольный треугольник O 1 B 1 M 1 , его гипотенуза

будет равна радиусу вращения точки В . На пересечении дуги радиусом O 1 M 1 с продолжением перпендикуляра O 1 B 1 определяем новое положение точки B 1 – B 1 ‘. Затем определяем положение точки С , причем можно не определять радиус точки С , а найти положение точки C 1 в пересечении двух прямых, одна из которых является перпендикуляром, проведенным из точки C 1 к прямой A 1 D 1 , а другая проходит через найденную точку B 1 ‘ и точку D 1 . Горизонтальная проекция A 1 B 1 ‘ C 1 ‘ равна самому треугольнику АВС , так как после вращения плоскость треугольника АВС параллельна плоскости π 1 .

2.4 Способ совмещения

Способ совмещения является частным случаем способа вращения плоскости вокруг горизонтали или фронтали, когда за ось вращения принимается горизонтальный или фронтальный след плоскости.

Сущность способа совмещения состоит в том, что плоскость R

(рис. 60) вращением вокруг следа Rπ 1 совмещается с плоскостью проекций π 1. Горизонтальный след плоскости (ось вращения) при этом остается на месте.

Для нахождения совмещенного положения фронтального следа Rπ 2 плоскости R определяют совмещенное положение некоторой точки N, произвольно взятой на Rπ 2 . Эта точка при совмещении плоскости R с плоскостью проекций π 1 будет перемещаться в пространстве по дуге окружности радиуса ON, лежащей в плоскости P, перпендикулярной горизонтальному следу Rπ 1 плоскости R , т. е. оси вращения. Совмещенное положение N 1 точки N определилось в пересечении этой дуги с горизонтальным следом Pπ 1 плоскости P. Прямая, проходящая через точки R х и N 2 ‘, и есть R π 2 ’ .

На рис. 61 это же построение выполнено на эпюре. Истинная величина радиуса вращения ON о точки N определена способом прямоугольного треугольника. Когда точка схода следов R х плоскости находится в пределах чертежа (рис. 61), совмещенное положение точки N можно найти более простым построением. Так как R x N 2 = R х N 2 ‘ то, проведя из точки R х дугу радиуса R x N 2 до пересечения со следом P π 1 , найдем совмещенное положение точки N. Чтобы совместить с плоскостью π 1 точку, принадлежащую плоскости R , но не лежащую на следе R π 2 ,нужно найти совмещенное положение горизонтали, проходящей через заданную точку, и из горизонтальной проекции точки опустить перпендикуляр на след R π 1 до пересечения с совмещенной горизонталью (точка А на рис. 61).

При помощи способа совмещения можно построить в плоскости общего положения фигуру, форма и размеры которой заданы.

Определить натуральную величину треугольника АВС , лежащего в плоскости S , если задана его горизонтальная проекция (рис.62)

Задачу решаем в несколько этапов (рис.63):

1. Строим фронтальную проекцию треугольника АВС .

Недостающие проекции точек треугольника АВС определяем при помощи горизонталей плоскости S .

2. Совмещаем плоскость S с горизонтальной плоскостью проекций. Для этого фронтальном следе плоскости

Источник