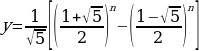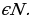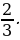Лекция последовательности способы задания

Лекция «Числовая последовательность и ее предел»
учебно-методический материал

Лекция «Числовая последовательность и ее предел» для студентов 2 курса специальности «Компьютерные системы и комплексы»

Скачать:

Вложение	Размер
lektsiya_1._posledovatelnosti.pdf	374.19 КБ

Предварительный просмотр:

Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com

По теме: методические разработки, презентации и конспекты

Виды и формы контроля освоения программ среднего (полного) общего образования в пределах ОПОП НПО/СПО согласно требованиям ФГОС нового поколения представлены в виде таблицы.

Данное учебное пособие предназначено для преподавателей и студентов2 курса. Пособие составлено в соответствии с рабочей программой учебнойдисциплины «Математика» по специальностям 080114, 100701. Учеб.

Презентация к уроку Предел последовательности.

Тип занятия: комбинированный.Формы занятия: индивидуальная.Оборудование: проектор, компьютер, доска, рабочие тетради.Продолжительность занятия: 90 мин.Цели занятия:Дидактическая цель. Познакомить обуч.

Для проведения занятий по математике студентов 2 курса.

Практическая работа «Нахождение пределов функций с помощью замечательных пределов&quot.

Вычисление пределов функции с использованием 1-го и 2-го замечательного предела.

Источник

Лекция по теме: «Числовая последовательность и способы её задания»

ТО 207 на 01.11.21 г. законспектировать лекцию и выполнить задания!

Просмотр содержимого документа
«Лекция по теме: «Числовая последовательность и способы её задания»»

ТО 207 законспектировать и выполнить задания! Прислать на почту: [email protected]

Тема: Определение числовой последовательности и способы её задания.

— знать, что такое числовая последовательность;

— способы задания числовой последовательности;

— уметь различать различные способы задания числовых последовательностей.

Краткие теоретические и учебно-методические материалы по теме практической работы (законспектировать!)

Определение 1. Функцию y = f(x), x 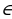N называют функцией натурального аргумента или числовой последовательностью и обозначают: y = f(n) или y₁, y₂, y₃, . y_n, . или (y_n).

В данном случае независимая переменная – натуральное число.

Способы задания числовой последовательности.

Словесный способ: правила задания последовательности описываются словами, без указания формул или когда закономерности между элементами последовательности нет.

Пример 1. Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, . .

Пример 2. Произвольный набор чисел: 1, 4, 12, 25, 26, 33, 39, . .

Пример 3. Последовательность чётных чисел 2, 4, 6, 8, 10, 12, 14, 16, . .

Аналитический способ: любой n-й элемент последовательности можно определить с помощью формулы.

Пример 1. Последовательность чётных чисел: y = 2n.

Пример 2. Последовательность квадрата натуральных чисел: y = n 2

1, 4, 9, 16, 25, . n 2 , . .

Пример 3. Стационарная последовательность: y = C

Частный случай: y = 5; 5, 5, 5, . 5, . .

Пример 4. Последовательность y = 2 n

2, 2 2 , 2 3 , 2 4 , . 2 n , . .

Рекуррентный способ: указывается правило, позволяющее вычислить n-й элемент последовательности, если известны её предыдущие элементы.

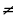
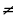
Пример 2. Геометрическая прогрессия: b₁= b, b_n+1= b_n q, где b и q – заданные числа, b 0, q 0; q – знаменатель геометрической прогрессии. Пусть b₁=23, q=½, тогда геометрическая прогрессия будет иметь вид: 23; 11,5; 5,75; 2,875; . .

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . .

Аналитически последовательность Фибоначчи задать трудно, но возможно. Формула, по которой определяется любой элемент этой последовательности, выглядит так:

Пример 1. Составить возможную формулу n-го элемента последовательности (y_n):

а) Это последовательность нечётных чисел. Аналитически эту последовательность можно задать формулой y = 2n+1.

б) Это числовая последовательность, у которой последующий элемент больше предыдущего на 4. Аналитически эту последовательность можно задать формулой

Каждый последующий элемент этой последовательности равен сумме двух предыдущих элементов.

Найдём несколько первых элементов последовательности.

Получаем последовательность: 1; 2; 4; 8; 16; 32; 64; . которую можно представить в виде

2 0 ; 2 1 ; 2 2 ; 2 3 ; 2 4 ; 2 5 ; 2 6 . .

n = 1; 2; 3; 4; 5; 6; 7. .

Анализируя последовательность, получаем следующую закономерность: y = 2 n -1 .

а) Сколько в ней положительных членов?

б) Найти наибольший элемент последовательности.

в) Есть в данной последовательности наименьший элемент?

Данная числовая последовательность – это функция вида y = -5x 2 +24x+36, где x

а) Найдём значения функции, при которых -5x 2 +24x+360. Решим уравнение -5x 2 +24x+36=0.

D = b 2 -4ac=1296, 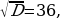X₁=6, X₂=-1,2.

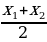
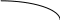
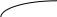
Уравнение оси симметрии параболы y = -5x 2 +24x+36 можно найти по формуле x= , получим: x=2,4.

Неравенство -5x 2 +24x+360 выполняется при -1,2 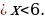В этом интервале находится пять натуральных чисел (1, 2, 3, 4, 5). Значит в заданной последовательности пять положительных элементов последовательности.

б) Наибольший элемент последовательности определяется методом подбора и он равен y₂=64.

в) Наименьшего элемента нет.

Задания для практической работы:

Из двух вариантов практической работы выберите свой вариант. Это зависит от начальной букв фамилии: А-К (1 вариант), Л-Я (2 ва­риант. При замене одного варианта другим практическая работа считается невыполненной.

1. Составьте возможную формулу n-го элемента последовательности (y_n), если последовательность имеет вид: 2, 4, 6, 8, 10, 12, . .

3. Найдите формулу n-го элемента и сумму первых 15 элементов арифметической прогрессии с первым элементом 3,4 и разностью 0,9.

4. Найдите сумму бесконечной геометрической прогрессии с первым членом 3,5 и знаменателем —

5. В арифметической прогрессии a₅= -150, a₆= -147. Найдите номер первого положительного элемента этой последовательности.

6. Укажите наиболее близкий к нулю элемент арифметической прогрессии

а) Сколько в ней положительных элементов?

б) Найти наибольший элемент последовательности.

в) Есть в данной последовательности наименьший элемент?

1. Составьте возможную формулу n-го элемента последовательности (y_n), если последовательность имеет вид: 7, 11, 15, 19, 23, . .

3. Найдите формулу n-го элемента и сумму первых 15 элементов арифметической прогрессии с первым элементом 3,5 и разностью 0,8.

4. Найдите сумму бесконечной геометрической прогрессии с первым членом 4,5 и знаменателем —

5. В арифметической прогрессии a₅= 160, a₆= 156. Найдите номер первого отрицательного элемента этой последовательности.

6. Укажите наиболее близкий к нулю элемент арифметической прогрессии

а) Сколько в ней положительных элементов?

б) Найти наибольший элемент последовательности.

в) Есть в данной последовательности наименьший элемент?

Источник

Лекция по теме»Последовательности. Способы задания и свойства числовых последовательностей. Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.»

Последовательности. Способы задания и свойства числовых последовательностей. Суммирование последовательностей. Бесконечно убывающая геометрическая прогрессия и ее сумма.

Сформировать понятие последовательности;

Рассмотреть способы задания и свойства числовых последовательностей.

Последовательностью называется функция, которая переводит множество натуральных чисел в некоторое множество :

Элемент называется первым членом последовательности , — вторым, . , — -ым или общим членом последовательности .

Задание. Для последовательности определить, чему равен третий член

Решение. Третьим элементом последовательности будет элемент, идущий третьим по счету, то есть для заданной последовательности имеем, что

Ответ.

Задание последовательности формулой ее общего члена

Обычно последовательность целесообразнее задавать формулой ее общего члена, которая позволяет найти любой член последовательности, зная его номер.

Задание. Найти формулу общего члена последовательности

Решение. Запишем каждый член последовательности в следующем виде:

Как видим, члены последовательности представляют собой произведение степени двойки, умноженной на последовательные нечетные числа, причем два возводится в степень, которая равна номеру рассматриваемого элемента.

Таким образом, делаем вывод, что

Ответ. Формула общего члена:

Задание. Найти 15 член последовательности, заданной формулой -го члена:

Решение. Для того чтобы найти , подставим в формулу общего члена значение . Получим:

Ответ.

Задание. Проверить, являются ли числа и членами последовательности

Решение. Число является членом последовательности , если существует такой номер , что :

Таким образом, число является первым и пятым членами заданной последовательности.

Проверим теперь, является ли число членом указанной последовательности . Рассуждая аналогично, как и для , получаем:

Таким образом, уравнение не имеет решение в натуральных числах , а значит, не является членом последовательности

Ответ. Число является первым и пятым членами заданной последовательности, а не является членом последовательности .

1. Последовательность задана аналитически, если задана формула ее n -го члена:

Пример. y _n = 2 n – 1 – последовательность нечетных чисел: 1, 3, 5, 7, 9, …

2. Описательный способ задания числовой последовательности состоит в том, что объясняется, из каких элементов строится последовательность.

«Все члены последовательности равны 1». Это значит, речь идет о стационарной последовательности 1, 1, 1, …, 1, ….

«Последовательность состоит из всех простых чисел в порядке возрастания». Таким образом, задана последовательность 2, 3, 5, 7, 11, …. При таком способе задания последовательности в данном примере трудно ответить, чему равен, скажем, 1000-й элемент последовательности.

3.Рекуррентный способ задания последовательности.

Другим способом задания последовательности является задание последовательности с помощью рекуррентного соотношения. В этом случае задается один или несколько первых элементов последовательности, а остальные определяются по некоторому правилу. Например, известен первый член последовательности и известно, что , то есть и так далее до нужного члена.

Примером рекуррентно заданной последовательности является последовательность чисел Фибоначчи — 1, 1, 2, 3, 5, 8, 13, . , в которой каждое последующее число, начиная с третьего, является суммой двух предыдущих: 2 = 1 + 1; 3 = 2 + 1 и так далее. Данную последовательность можно задать рекуррентно:

Задание. Последовательность задана при помощи рекуррентного соотношения . Выписать несколько первых членов этой последовательности.

Решение. Найдем третий член заданной последовательности:

Аналогично находим далее, что

и так далее.

1. Что называется числовой последовательностью?

Ответ : Множество чисел, элементы которого можно пронумеровать.

2. Приведи пример числовой последовательности.

3. Что называется членами числовой последовательности?

Ответ : Числа, составляющие числовую последовательность.

4. Что такое общий член числовой последовательности?

Ответ : ап называется общим членом последовательности ,а саму последовательность коротко обозначают через <ап>.

5. Как обозначают числовую последовательность?

Ответ : Обычно числовую последовательность обозначают малыми буквами латинского алфавита с индексами, указывающими на номер этого члена в последовательности: а ₁ ,а ₂ ,а ₃ ,а ₄ ,….,а _п ,…

5. Когда числовую последовательность считаются заданной?

Ответ : Если мы можем указать любой член последовательности.

Напишите первые пять членов последовательности.

3.

Ответ :

n=5, x ₅ =3*5 2 +2*5+1=3*25+10+1=75+11=86

Ответ :

№ 344. Напишите формулу общего члена последовательности натуральных чисел, кратных 3.

№ 345. Напишите формулу общего члена последовательности натуральных чисел, кратных 7.

№ 346 Напишите формулу общего члена последовательности натуральных чисел, которые при делении на 4 дают в остатке 1.

№ 347 Напишите формулу общего члена последовательности натуральных чисел, которые при делении на 5 дают в остатке 2.

№ 348 Напишите формулу общего члена последовательности.

3)

Ответ :

Ответ :

Источник