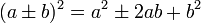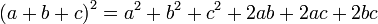Легкий способ возведения квадрата

Урок 7. Возведение в квадрат в уме

Умение считать в уме квадраты чисел может пригодиться в разных жизненных ситуациях, например, для быстрой оценки инвестиционных сделок, для подсчета площадей и объемов, а также во многих других случаях. Кроме того, умение считать квадраты в уме может служить демонстрацией ваших интеллектуальных способностей.

В этом уроке разобраны методики и алгоритмы, позволяющие научиться этому навыку.

Квадрат суммы и квадрат разности

Одним из самых простых способов возведения двузначных чисел в квадрат является методика, основанная на использовании формул квадрата суммы и квадрата разности:

Для использования этого метода необходимо разложить двузначное число на сумму числа кратного 10 и числа меньше 10. Например:

• 37 2 = (30+7) 2 = 30 2 + 2*30*7 + 7 2 = 900+420+49 = 1 369
• 94 2 = (90+4) 2 = 90 2 + 2*90*4 + 4 2 = 8100+720+16 = 8 836

Практически все методики возведения в квадрат (которые описаны ниже) основываются на формулах квадрата суммы и квадрата разности. Эти формулы позволили выделить ряд алгоритмов упрощающих возведение в квадрат в некоторых частных случаях.

Квадрат близкий к известному квадрату

Если число, возводимое в квадрат, находится близко к числу, квадрат которого мы знаем, можно использовать одну из четырех методик для упрощенного счета в уме:

На 1 больше:

Методика: к квадрату числа на единицу меньше прибавляем само число и число на единицу меньше.

• 31 2 = 30 2 + 31 + 30 = 961
• 16 2 = 15 2 + 15 + 16 = 225 + 31 = 256

На 1 меньше:

Методика: из квадрата числа на единицу больше вычитаем само число и число на единицу больше.

• 19 2 = 20 2 – 19 – 20 = 400 – 39 = 361
• 24 2 = 25 2 – 24 – 25 = 625 – 25 – 24 = 576

На 2 больше

Методика: к квадрату числа на 2 меньше прибавляем удвоенную сумму самого числа и числа на 2 меньше.

• 22 2 = 20 2 + 2*(20+22) = 400 + 84 = 484
• 27 2 = 25 2 + 2*(25+27) = 625 + 104 = 729

На 2 меньше

Методика: из квадрата числа на 2 больше вычитаем удвоенную сумму самого числа и числа на 2 больше.

• 48 2 = 50 2 – 2*(50+48) = 2500 – 196 = 2 304
• 98 2 = 100 2 – 2*(100+98) = 10 000 – 396 = 9 604

Все эти методики можно легко доказать, выведя алгоритмы из формул квадрата суммы и квадрата разности (о которых сказано выше).

Квадрат чисел, заканчивающихся на 5

Чтобы возвести в квадрат числа, заканчивающиеся на 5. Алгоритм прост. Число до последней пятерки, умножаем на это же число плюс единица. К оставшемуся числу приписываем 25.

• 15 2 = (1*(1+1)) 25 = 225
• 25 2 = (2*(2+1)) 25 = 625
• 85 2 = (8*(8+1)) 25 = 7 225

Это верно и для более сложных примеров:

• 155 2 = (15*(15+1)) 25 = (15*16)25 = 24 025

Квадрат чисел близких к 50

Считать квадрат чисел, которые находятся в диапазоне от 40 до 60, можно очень простым способом. Алгоритм таков: к 25 прибавляем (или вычитаем) столько, насколько число больше (или меньше) 50. Умножаем эту сумму (или разность) на 100. К этому произведению добавляем квадрат разности числа, возводимого в квадрат, и пятидесяти. Посмотрите работу алгоритма на примерах:

• 44 2 = (25-6)*100 + 6 2 = 1900 + 36 = 1936
• 53 2 = (25+3)*100 + 3 2 = 2800 + 9 = 2809

Квадрат трехзначных чисел

Возведение в квадрат трехзначных чисел может быть осуществлено при помощи одной из формул сокращенного умножения:

Нельзя сказать, что этот способ является удобным для устного счета, но в особо сложных случаях его можно взять на вооружение:

436 2 = (400+30+6) 2 = 400 2 + 30 2 + 6 2 + 2*400*30 + 2*400*6 + 2*30*6 = 160 000 + 900 + 36 + 24 000 + 4 800 + 360 = 190 096

Тренировка

Если вы хотите прокачать свои умения по теме данного урока, можете использовать следующую игру. На получаемые вами баллы влияет правильность ваших ответов и затраченное на прохождение время. Обратите внимание, что числа каждый раз разные.

Перед тем как начать игру, рекомендуем зарегистрироваться, чтобы результат был сохранен в вашей истории, и вы смогли бы видеть собственный прогресс.

Напоминаем, что для полноценной работы сайта вам необходимо включить cookies, javascript и iframe. Если вы ввидите это сообщение в течение долгого времени, значит настройки вашего браузера не позволяют нашему порталу полноценно работать.

Источник

Быстрое возведение чисел в квадрат без калькулятора

21 сентября 2013

Сегодня мы научимся быстро без калькулятора возводить большие выражения в квадрат. Под большими я подразумеваю числа в пределах от десяти до ста. Большие выражения крайне редко встречаются в настоящих задачах, а значения меньше десяти вы и так умеете считать, потому что это обычная таблица умножения. Материал сегодняшнего урока будет полезен достаточно опытным ученикам, потому что начинающие ученики просто не оценят скорость и эффективность этого приема.

Для начала давайте разберемся вообще, о чем идет речь. Предлагаю для примера сделать возведение произвольного числового выражения, как мы обычно это делаем. Скажем, 34. Возводим его, умножив само на себя столбиком:

1156 — это и есть квадрат 34.

Проблему данного способа можно описать двумя пунктами:

1) он требует письменного оформления;

2) в процессе вычисления очень легко допустить ошибку.

Сегодня мы научимся быстрому умножению без калькулятора, устно и практически без ошибок.

Итак, приступим. Для работы нам потребуется формула квадрата суммы и разности. Давайте запишем их:

Что нам это дает? Дело в том, что любое значение в пределах от 10 до 100 представимо в виде числа $a$, которое делится на 10, и числа $b$, которое является остатком от деления на 10.

Например, 28 можно представить в следующем виде:

Аналогично представляем оставшиеся примеры:

Что дает нам такое представление? Дело в том, что при сумме или разности, мы можем применить вышеописанные выкладки. Разумеется, чтобы сократить вычисления, для каждого из элементов следует выбрать выражение с наименьшим вторым слагаемым. Например, из вариантов $20+8$ и $30-2$ следует выбрать вариант $30-2$.

Аналогично выбираем варианты и для остальных примеров:

Почему следует стремиться к уменьшению второго слагаемого при быстром умножении? Все дело в исходных выкладках квадрата суммы и разности. Дело в том, что слагаемое $2ab$ с плюсом или с минусом труднее всего считается при решении настоящих задач. И если множитель $a$, кратный 10, всегда перемножается легко, то вот с множителем $b$, который является числом в пределах от одного до десяти, у многих учеников регулярно возникают затруднения.

Можете самостоятельно попробовать рассчитать оба разложения, и вы убедитесь, что разложение с наименьшим вторым слагаемым считается проще. А мы перейдем к примерам, которые посчитаем без калькулятора:

Вот так за три минуты мы сделали умножение восьми примеров. Это меньше 25 секунд на каждое выражение. В реальности после небольшой тренировки вы будете считать еще быстрее. На подсчет любого двухзначного выражения у вас будет уходить не более пяти-шести секунд.

Но и это еще не все. Для тех, кому показанный прием кажется недостаточно быстрым и недостаточно крутым, предлагаю еще более быстрый способ умножения, который однако работает не для всех заданий, а лишь для тех, которые на единицу отличаются от кратных 10. В нашем уроке таких значений четыре: 51, 21, 81 и 39.

Казалось бы, куда уж быстрее, мы и так считаем их буквально в пару строчек. Но, на самом деле, ускориться можно, и делается это следующим образом. Записываем значение, кратное десяти, которое наиболее близкое нужному. Например, возьмем 51. Поэтому для начала возведем пятьдесят:

Значения, кратные десяти, поддаются возведению в квадрат намного проще. А теперь к исходному выражению просто добавляем пятьдесят и 51. Ответ получится тот же самый:

И так со всеми числами, отличающимися на единицу.

Если значение, которое мы ищем, больше, чем то, которое мы считаем, то к полученному квадрату мы прибавляем числа. Если же искомое число меньше, как в случае с 39, то при выполнении действия, из квадрата нужно вычесть значение. Давайте потренируемся без использования калькулятора:

Как видите, во всех случаях ответы получаются одинаковыми. Более того, данный прием применим к любым смежным значениям. Например:

При этом нам совсем не нужно вспоминать выкладки квадратов суммы и разности и использовать калькулятор. Скорость работы выше всяких похвал. Поэтому запоминайте, тренируйтесь и используйте на практике.

Ключевые моменты

С помощью этого приема вы сможете легко делать умножение любых натуральных чисел в пределах от 10 до 100. Причем все расчеты выполняются устно, без калькулятора и даже без бумаги!

Для начала запомните квадраты значений, кратных 10:

Далее — выкладки квадрата суммы или разности, в зависимости от того, к какому опорному значению ближе наше искомое выражение. Например:

Как считать еще быстрее

Но это еще не все! С помощью данных выражений моментально можно сделать возведение в квадрат чисел, «смежных» с опорными. Например, мы знаем 152 (опорное значение), а надо найти 142 (смежное число, которое на единицу меньше опорного). Давайте запишем:

Обратите внимание: никакой мистики! Квадраты чисел, отличающиеся на 1, действительно получаются из умножения самих на себя опорных чисел, если вычесть или добавить два значения:

Почему так происходит? Давайте запишем формулу квадрата суммы (и разности). Пусть $n$ — наше опорное значение. Тогда они считаются так:

— это и есть формула.

— аналогичная формула для чисел, больших на 1.

Надеюсь, данный прием сэкономит вам время на всех ответственных контрольных и экзаменах по математике. А у меня на этом все. До встречи!

Источник

Быстрое возведение чисел от 1 до 100 в квадрат

Вдохновленный этой статьей, решил поделиться с вами способом быстрого возведения в квадрат. Возведение в квадрат более редкая операция, нежели умножение чисел, но под нее существуют довольно интересные правила.

*квадраты до сотни

Для того, чтобы бездумно не возводить в квадрат по формуле все числа, нужно максимально упростить себе задачу следующими правилами.

Правило 1 (отсекает 10 чисел)

Для чисел, оканчивающихся на 0.
Если число заканчивается на 0, умножить его не сложнее, чем однозначное число. Стоит лишь дописать пару нулей.

В таблице отмечены красным.

Правило 2 (отсекает 10 чисел)

Для чисел, оканчивающихся на 5.
Чтобы возвести в квадрат двузначное число, оканчивающееся на 5, нужно умножить первую цифру (x) на (x+1) и дописать к результату “25”.

В таблице отмечены зеленым.

Правило 3 (отсекает 8 чисел)

Для чисел от 40 до 50.

Достаточно трудно, верно? Давайте разберем пример:

В таблице отмечены светло-оранжевым.

Правило 4 (отсекает 8 чисел)

Для чисел от 50 до 60.

Тоже достаточно трудно для восприятия. Давайте разберем пример:

В таблице отмечены темно-оранжевым.

Правило 5 (отсекает 8 чисел)

Для чисел от 90 до 100.

Похоже на правило 3, но с другими коэффициентами. Давайте разберем пример:

В таблице отмечены темно-темно-оранжевым.

Правило №6 (отсекает 32 числа)

Необходимо запомнить квадраты чисел до 40. Звучит дико и трудно, но на самом деле до 20 большинство людей знают квадраты. 25, 30, 35 и 40 поддаются формулам. И остается лишь 16 пар чисел. Их уже можно запомнить при помощи мнемоники (о которой я также хочу рассказать позднее) или любыми другими способами. Как таблицу умножения 🙂
В таблице отмечены синим.

Вы можете запомнить все правила, а можете запомнить выборочно, в любом случае все числа от 1 до 100 подчиняются двум формулам. Правила же помогут, не используя эти формулы, быстрее посчитать больше 70% вариантов. Вот эти две формулы:

Формулы (осталось 24 числа)

Для чисел от 25 до 50

Для чисел от 50 до 100

Конечно не стоит забывать про обычную формулу разложения квадрата суммы (частный случай бинома Ньютона):

UPDATE
Произведения чисел, близких к 100, и, в частности, их квадраты, также можно вычислять по принципу «недостатков до 100»:

Словами: из первого числа вычитаем «недостаток» второго до сотни и приписываем двузначное произведение «недостатков».

Для квадратов, соответственно, еще проще.

Возведение в квадрат, возможно, не самая полезная в хозяйстве вещь. Не сразу вспомнишь случай, когда может понадобиться квадрат числа. Но умение быстро оперировать числами, применять подходящие правила под каждое из чисел отлично развивает память и «вычислительные способности» вашего мозга.

Кстати, думаю, все читатели хабры знают, что 64^2 = 4096, а 32^2 = 1024.
Многие квадраты чисел запоминаются на ассоциативном уровне. Например, я легко запомнил 88^2 = 7744, из-за одинаковых чисел. У каждого наверняка найдутся свои особенности.

Две уникальные формулы я впервые нашел в книге «13 steps to mentalism», которая мало связана с математикой. Дело в том, что раньше (возможно, и сейчас) уникальные вычислительные способности были одним из номеров в сценической магии: фокусник рассказывал байку о том, как он получил сверхспособности и в доказательство этого моментально возводит числа до сотни в квадрат. В книге так же указаны способы возведения в куб, способы вычитания корней и кубических корней.

Если тема быстрого счета интересна — буду писать еще.
Замечания об ошибках и правки прошу писать в лс, заранее спасибо.

Источник

Легкий способ возведения квадрата

Введение.

Математика – очень древняя наука. Многие понятия, правила, законы, формулы уже известны давно, и открыть что-то новое, просто невозможно. Всё равно на уроке математики мы открываем для себя новые знания. Из года в год наши знания увеличиваются. Например, при изучении темы «Степень» узнали, что произведение одинаковых множителей можно записать, как степень данного числа. Так мы познакомились с квадратом и кубом числа.

Устно возводить в квадрат однозначное число легко, для этого надо знать всего лишь таблицу умножения. А как устно возвести в квадрат двузначное число, меня очень заинтересовало.

Умея это выполнять, мы откажемся от письменного умножения. Конечно, можно посмотреть в таблицу квадратов, но она не всегда под руками.

Цель проекта: Поиск приёмов быстрого возведения чисел в квадрат.

Задачи: 1) Познакомиться с историей возникновения степени числа.

2) Изучить приёмы быстрого возведения чисел в квадрат.

3) Вывести свой способ возведения чисел в квадрат.

4) Выбрать из всех самый оптимальный способ.

Гипотеза: Применение приёмов быстрого возведения чисел в квадрат облегчает вычисления, повышает вычислительную культуру учащихся. Возводить в квадрат легко и просто.

Объект исследования: приёмы быстрого возведения чисел в квадрат.

Методы исследования: Анализ литературы. Поисковый метод. Сравнение.

Актуальность проекта: Во все времена умение производить в уме различные вычисления вызывает восхищение, это отличное упражнение, позволяющее поддержать мозг в состоянии «боевой готовности»[1]. Освоение способов устного возведения чисел в квадрат усиливает интерес к математике, развивает внимание, мышление, память, эрудицию и математические способности.

История возникновения квадрата числа.

Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней[5].

В своей знаменитой «Арифметике» Диофант Александрийский [2] описывает первые натуральные степени чисел так:

«Все числа… состоят из некоторого количества единиц; ясно, что они продолжаются, увеличиваясь до бесконечности. …среди них находятся: квадраты, получающиеся от умножения не­которого числа самого на себя; это же число называется стороной квадрата, затем кубы, получающиеся от умножения квадратов на их сторону, далее квадрато-квадраты — от умножения квадратов самих на себя, далее квадрато-кубы, получающиеся от умно­жения квадрата на куб его стороны, далее кубо-кубы — от умножения кубов самих на себя».

Прошло много времени и у Рене Декарта[3] в его «Геометрии» (1637) мы находим современное обозначение степеней а?, а. Любопытно, что Декарт считал, что а*а не занимает больше места, чем а 2 и не пользовался этим обозначением при записи произведения двух одинаковых множителей.

Немецкий ученый Лейбниц[4] считал, что упор должен быть сделан на необходимости применения символики для всех записей произведений одинаковых множителей и применял знак а 2 [5].

Приёмы быстрого возведения чисел в квадрат.

Учись считать быстро! Для овладения этим навыком любому человеку нужны:

Давайте познакомимся с некоторыми приёмами возведения в квадрат двузначных чисел, которые выполняются почти мгновенно[1].

Возведение в квадрат числа, оканчивающегося на 5.

1. 35 2 = 3 · (3 + 1) · 100 + 5 · 5 = 1200 + 25 = 1225.
2. 75 2 = 5600 + 25 = 5625.
3. 85 2 = 7225.

Чтобы возвести в квадрат число, оканчивающееся цифрой 5, надо умножить количество его десятков на следующее за ним число и приписать к произведению 25.

Возведение в квадрат числа, первая цифра которого равна 5.

• 52 2 = (5 · 5 + 2) · 100 + 2 · 2 = 2700 + 4 = 2704.
• 54 2 = (25 + 4) · 100 + 16 = 2916.
• 58 2 = 3300 + 64 = 3364.
• 51 2 = 2601.

Чтобы возвести в квадрат двузначное число, первая цифра которого равна 5, надо к 25 прибавить число единиц и приписать квадрат числа единиц.

• Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.

Возведение в квадрат числа, оканчивающегося на 1.

1. 71 2 ; 71→70→70 2 = 4900; 71 2 = 4900 + 71 + 70 = 5041.
2. 41 2 = 1600 + 41 + 40 = 1881.
3. 81 2 = 6400 + 161 = 6561.

При возведении в квадрат числа, оканчивающегося на 1, нужно округлить число до десятков, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное при округлении.

Возведение в квадрат числа, оканчивающегося на 9.

1. 59 2 ; 59 → 60→60 2 =3600; 59 2 = 3600 – 60 – 59 = 3600 – 119 = 3481.
2. 29 2 = 900 – 29 – 30 = 841.
3. 79 2 = 6400 – 159 = 6241.
4. При возведении в квадрат числа, оканчивающегося на 9, нужно его округлить до десятков, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное при округлении.

Возведение в квадрат числа, оканчивающегося на 4.

1. 84 2 ; 84→85→85 2 = 7225; 84 2 = 7225 – 84 – 85 = 7225 – 169 = 7056.
2. 34 2 = 1225 – 34 – 35 = 1225 – 69 = 1156.
3. 74 2 = 5625 – 149 = 5476.

При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.

Возведение в квадрат числа, оканчивающегося на 6.

1. 56 2 ; 56→55→55 2 = 3025; 56 2 = 3025 + 56 + 55 = 3025 + 111 = 3136.
2. 36 2 = 1225 + 36 + 35 =1296.
3. 76 2 = 5625 + 151 = 5776.

При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат, и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.

Возведение в квадрат числа, близкого к 50.

а) Для чисел от 40 до 50 (числа пятого десятка). Опорное число – 15.

1) 44 2 = (15 + 4) · 100 + (50 – 44) 2 = 1900 + 36 = 1936.

2) 43 2 = 18 · 100 + 7 2 = 1800 + 49 = 1849.

3) 48 2 = 2300 + 4 = 2304.

• Чтобы возвести в квадрат числа пятого десятка (41, 42, 43, 44, 45, 46, 47, 48, 49), надо к числу 15 прибавить число единиц числа, затем к полученной сумме приписать квадрат дополнения данного числа до 50.

б) Для чисел от 25 до 40 и до 50. Опорное число – 25.

1) 37 2 = (37 – 25) · 100 + (50 – 37) 2 = 12 · 100 + 13 2 = 1200 + 169 = 1369.

Для этого приёма надо знать квадраты чисел от 1 до 25.

2) 28 2 = 3 · 100 + 22 2 = 300 + 484 = 784.

3) 46 2 = 2100 + 16 = 2116.

4) 39 2 = 1400 + 121 = 1521.

• Чтобы возвести в квадрат число от 25 до 50, надо из данного числа вычесть 25, результат умножить на 100 и прибавить квадрат дополнения данного числа до 50.

в) Для чисел от 50 до 60 (числа шестого десятка). Опорное число – 25.

1) 57 2 = (25 +7) · 100 + (57 – 50) 2 = 32 · 100 + 7 2 = 3200 + 49 = 3249.

2) 52 2 = 2700 + 4 = 2704.

• Чтобы возвести в квадрат число шестого десятка (51, 52, 53, 54, 55, 56, 57, 58, 59), надо к 25 прибавить число единиц, затем к полученной сумме приписать квадрат разности данного числа и 50.
• Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.

г) Для чисел от 50 до 60 и до 75. Опорное слово – 25.

Для этого приёма надо знать квадраты чисел от 1 до 25.

1) 58 2 = (58 – 25) · 100 + (58 – 50) 2 = 33 · 100 + 8 2 = 3300 + 64 = 3364.

2) 71 2 = 46 · 100 + 21 2 = 4600 + 441 = 5041.

• Чтобы возвести в квадрат числа от 50 до 75, надо из данного числа вычесть 25, результат умножить на 100 и прибавить квадрат разности данного числа и 50.

Возведение в квадрат числа, близкого к 100.

97 2 = (97 – 3) · 100 + 3 2 = 9400 + 9 = 9409, где 3 – дополнение 97 до 100.

94 2 = (94 – 6) · 100 + 6 2 = 8800 + 36 = 8836.

• Чтобы возвести в квадрат число, близкое к 100, надо из него вычесть дополнение данного числа до 100, к результату приписать квадрат дополнения.
• Если квадрат дополнения является однозначным числом, то перед ним записать цифру нуль.

Возведение в квадрат любого двузначного числа.

а) Метод «пирамидка».

38 2 = (30 + 8) 2 = (30 + 8) · (30 + 8) = (30 + 8) · 30 + (30 + 8) · 8 = 30 · 30 + 8 · 30 +

+ 30 · 8 + 8 · 8 = 3 · 3 · 100 + 3 · 8 · 10 + 3 · 8 · 10 + 8 · 8 = 3 2 · 100 + 3 · 8 · 2 · 10 + + 8 2 = 9 · 100 + 48 · 10 + 64 = 964 + 480 = 1444.

Можно оформить решение так:

27 2 = 449 + 280 = 729.

84 2 = 6416 + 640 = 7056.

б) Метод «перекидки».

42 2 = 42 · 42 = (42 + 2) · 40 + 2 2 = 44 · 40 + 4 = 1760 + 4 = 1764

78 2 = (78 + 8) · 70 + 64 = 86 · 70 + 64 = 6020 + 64 = 6084.

в) Метод «округления».

1) Для чисел, у которых цифра единиц больше 5:

47 2 = 47 · 47 = 50 · (47 – 3) + 3 2 = 50 · 44 + 9 = 2200 + 9 = 2209.

26 2 = 30 · 22 + 16 = 660 + 16 = 676.

1) Для чисел, у которых цифра единиц меньше 5:

73 2 = 73 · 73 = 70 · (73 + 3) + 3 2 = 70 · 76 + 9 = 5320 + 9 = 5329.

82 2 = 80 · 84 + 4 = 6720 + 4 = 6724.

г) Метод замены квадрата числа произведением.

29 2 = (29 – 9) · (29 + 9) + 9 2 = 20 · 38 + 81 = 760 + 81 = 841.

86 2 = (86 – 6) · (86 + 6) + 6 2 = 80 · 92 + 36 = 7360 + 36 = 7396.

54 2 = 50 · 58 + 16 = 2900 + 16 = 2916.

д) Метод понижения числа на единицу.

28 2 = (28 – 1) 2 + 28 + (28 – 1) = 27 2 + 28 + 27 = 729 + 55 = 784.

56 2 = 55 2 + 56 + 55 = 3025 + 111 = 3136.

Минус этого приёма в том, что квадрат данного двузначного числа выражаем через квадрат числа на единицу меньше, который надо либо вычислять, либо снова понижать, и так до бесконечности.

Возведение в квадрат любого двузначного числа по методу Алины.

Приёмов возведения двузначных чисел в квадрат много и все они разные. Для каждой группы чисел надо знать своё правило, а удержать все правила в уме иногда невозможно.

Собирая материал для проекта, мне захотелось вывести свой приём быстрого возведения двузначного числа в квадрат.

Очень понравился приём возведения в квадрат чисел, оканчивающихся на 5. Он быстрый и понятный. А можно ли этот приём применить для любого числа? Изучая литературу, я нигде этого способа не увидела. Применяя его для любых двузначных чисел, вот что у меня получилось.

Напомню: 35 2 = 3 · (3 + 1) · 100 + 5 2 = 1200 + 25 = 1225.

Возведём по этому способу в квадрат число 36.

Мы знаем, что 36 2 = 1296.

3 · (3 + 1) · 100 + 6 2 = 1200 + 36 = 1236, но 1236 1296. Число 1236 2 = 3 · 4 · 100 + 6 2 + 30 · 2 = 1236 + 60 = 1296.

Рассмотрим другие примеры.

56 2 = 5 · 6 · 100 + 6 2 + 50 · 2 = 3000 + 36 + 100 = 3036 + 100 = 3136.

46 2 = 2036 + 40 · 2 = 2036 + 80 = 2116.

Я много раз возводила числа в квадрат и увидела такую закономерность:

1. Выпишем цифры 1, 2, 3, 4, 5, 6, 7, 8, 9.
2. В этом ряду цифра 5 занимает середину; 4 и 6 отличаются от 5 на 1, они стоят на первом месте от 5; 3 и 7 – на втором; 2 и 8 – на третьем; 1 и 9 на четвёртом.

Пусть, например, надо возвести в квадрат число 39. Цифра 9 стоит на четвёртом месте от цифры 5, число 4 удваиваем, это будет 8, а теперь применяем приём:

39 2 = 3 · 4 · 100 + 9 2 + 30 · 8 = 1200 + 81 + 240 = 1281 + 240 = 1521.

240 можно представить так: 30 · 2 · 4, то есть десятки числа удвоить и умножить на номер места цифры единиц от цифры 5.

А как возвести в квадрат число, если цифра единиц меньше 5. Например, 73 2 .

Число 73 2 = 5329;

73 2 = 5609 – применяя приём возведения в квадрат для числа, оканчивающегося на 5. Но 5329 ≠ 5609.

х = 280, где 280 = 70 · 2 · 2, первая двойка удваивает число десятков в числе; вторая двойка обозначает номер места цифры 3 от цифры 5.

Эврика! Способ найден!

73 2 = 7 · 8 ·100 + 3 · 3 – 70 · 2 · 2 = 5609 – 280 = 5329.

Можно оформить решение и так:

• Чтобы возвести любое двузначное число в квадрат, надо количество десятков умножить на следующее число и приписать квадрат числа единиц. К полученному результату прибавить (или из полученного результата вычесть) удвоенное произведение десятков числа, умноженное на порядковый номер места цифры единиц в числовом ряду 1₄, 2₃, 3₂, 4₁, 5, 6₁, 7₂, 8₃, 9₄ от цифры 5.
• Если квадрат числа единиц является однозначным числом, то перед ним записать цифру нуль.

Какой приём возведения двузначного числа в квадрат наиболее простой? Для себя я выбрала два приёма. Мне они оба понятные и несложные.

1. 68 2 = 6 2 100 + 8 2 + 60 · 8 + 60 · 8 = 3664 + 480 + 480 = 3664 + 960 = 4624.
2. 68 2 = 6 · 7 · 100 + 8 2 + 60 ·2 · 3 = 4264 + 360 = 4624.

Какой приём выберите вы, думайте сами. Вам решать.

Заключение.

Владение приёмами быстрого возведения двузначного числа в квадрат даёт возможность выбрать в каждом отдельном случае наиболее рациональные и эффективные пути вычислений, что приводит:

• к сокращению времени на вычисления;
• к защите от массы вычислительных ошибок;
• к ведению записи в строчку и отказа от традиционного письменного умножения.

Считаю, что возводить двузначные числа в квадрат легко и просто. Гипотеза доказана.

Умение считать в уме остаётся полезным навыком для современного человека, несмотря на то, что он владеет всевозможными устройствами, способными считать за него.

Возможность обходиться без калькулятора и в нужный момент оперативно решить поставленную арифметическую задачу – это здорово[1]!

Источник