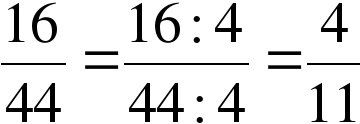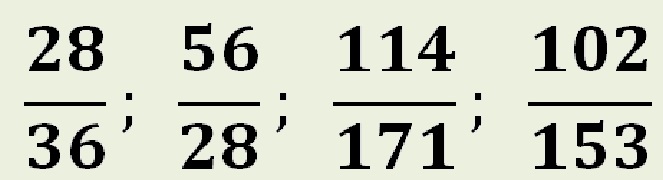Легкий способ сокращать дроби

Сокращение дроби.

Мы уже познакомились с основным свойством дроби (см. статью здесь). И знаем, как получить дробь, равную данной. Но сегодня мы поговорим о ДЕЛЕНИИ дроби на одно и то же число.

Деление числителя и знаменателя на одно и то же натуральное число называется СОКРАЩЕНИЕМ ДРОБИ. Но при этом – дроби остаются РАВНЫМИ.

Как сокращать дроби? Будем разбираться.

Итак, сокращение дроби – это действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Сокращение дроби выполняют для того, чтобы ее упростить.

Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же натуральное число, которое будет называться общим делителем.

Например, дана дробь 2/6.

На какие числа можно разделить 2? 2 делится на 1, 2. На какие числа можно разделить 6? 6 делится на 1, 2, 3, 6.

Но, мы знаем, что если дробь разделить на 1, то будет та же самая дробь. Поэтому на 1 не сокращают!

Теперь посмотрим на делители чисел 2 и 6. Сравним их:

Найдем одинаковые делители – это только число 2. Значит, мы можем разделить числитель и знаменатель нашей дроби только на 2.

Дробь 1/3 сократить нельзя.

Посмотрим на дробь 16/44. 16 делится на 2, 4, 8, 16. 44 делится на 2, 4, 11, 44. Одинаковые делители – 2, 4.

Разделим дробь на 2 — 16:2/44:2 = 8/22. Эту дробь можно еще сократить на 2. 8/22 = 8:2/22:2 = 4/11. Это очень долго, поэтому будем сокращать сразу на 4.

Дробь 4/11 сократить нельзя.

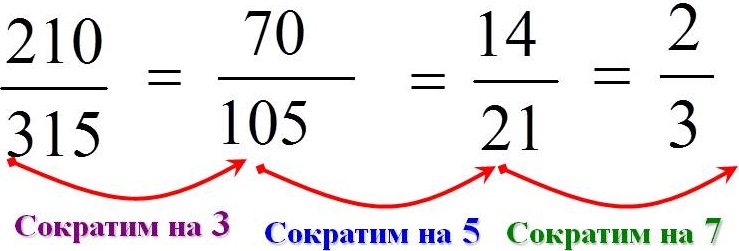
Рассмотрим дробь с большими числами: 210/315.

210 делится на 2, 3, 5, 7, 10, 30, 70, 105, 210.

315 делится на 3, 5, 7, 9, 15, 21, 63, 105, 315.

Общие делители: 3, 5, 7, 105. Будем сокращать дробь постепенно:

Мы видим, что если сокращать поочереди на все общие числители, начиная с меньшего, очень долго. Поэтому для удобства принято сокращать дробь сразу на больший числитель. Т.е. 210/315 = 210:105 / 315:105 = 2/3 Полученную дробь 2/3 сократить нельзя.

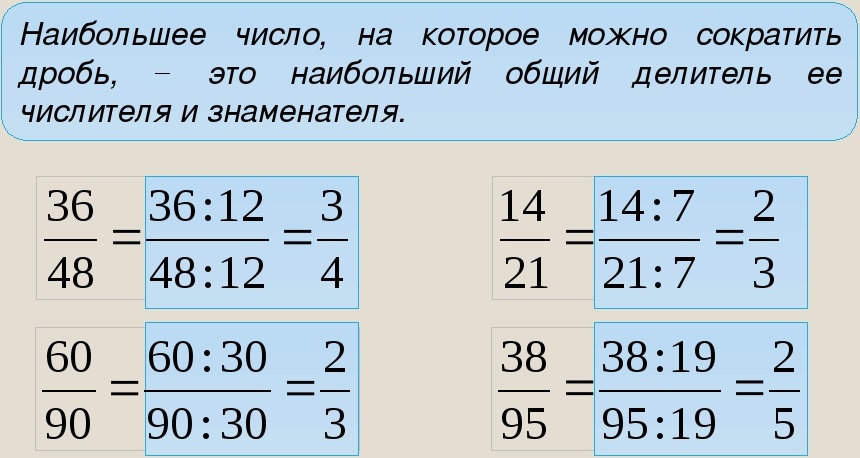
Наибольший общий делитель называют сокращенно — НОД.

Бывают случаи, когда общего делителя нет. Например, у дробей 3/59, 6/31, 11/23 и т.д. Тогда говорят о том, что эти дроби не подлежат сокращению.

Дроби, которые сократить НЕЛЬЗЯ называются НЕСОКРАТИМЫМИ, а числитель и знаменатель называют ВЗАИМНО-ПРОСТЫМИ.

Т.е. наша задача превратить любую дробь в несократимую. Итак, мы познакомились в двумя способами сокращения дробей:

Проверка: 28/36 – наибольший общий делитель (НОД) = 4, значит 28:4/36:4 = 7/9;

56/28 – НОД = 28, значит, 56:28/28:28 = 2/1 = 2;

114/171 – НОД = 57, значит, 114:57/171:57 = 2/3;

102/153 – НОД = 51, значит, 102:51/153:51 = 2/3.

Насколько публикация полезна?

Нажмите на звезду, чтобы оценить!

Средняя оценка 5 / 5. Количество оценок: 72

Источник

Сокращение дробей: правила и примеры

Разберемся в том, что такое сокращение дробей, зачем и как сокращать дроби, приведем правило сокращения дробей и примеры его использования.

Что такое «сокращение дробей»

Сократить дробь — значит разделить ее числитель и знаменатель на общий делитель, положительный и отличный от единицы.

В результате такого действия получится дробь с новым числителем и знаменателем, равная исходной дроби.

К примеру, возьмем обыкновенную дробь 6 24 и сократим ее. Разделим числитель и знаменатель на 2 , в результате чего получим 6 24 = 6 ÷ 2 24 ÷ 2 = 3 12 . В этом примере мы сократили исходную дробь на 2 .

Приведение дробей к несократимому виду

В предыдущем примере мы сократили дробь 6 24 на 2 , в результате чего получили дробь 3 12 . Нетрудно заметить, что эту дробь можно сократить еще. Как правило, целью сокращения дробей является получение в итоге несократимой дроби. Как привести дробь к несократимому виду?

Это можно сделать, если сократить числитель и знаменатель на их наибольший общий делитель (НОД). Тогда, по свойству наибольшего общего делителя, в числителе и в знаменателе будут взаимно простые числа, и дробь окажется несократимой.

a b = a ÷ Н О Д ( a , b ) b ÷ Н О Д ( a , b )

Приведение дроби к несократимому виду

Чтобы привести дробь к несократимому виду нужно ее числитель и знаменатель разделить на их НОД.

Вернемся к дроби 6 24 из первого примера и приведем ее к несократимому виду. Наибольший общий делитель чисел 6 и 24 равен 6 . Сократим дробь:

6 24 = 6 ÷ 6 24 ÷ 6 = 1 4

Сокращение дробей удобно применять, чтобы не работать с большими цифрами. Вообще, в математике существует негласное правило: если можно упростить какое-либо выражение, то нужно это делать. Под сокращением дроби чаще всего подразумевают ее приведение к несократимому виду, а не просто сокращение на общий делитель числителя и знаменателя.

Правило сокращения дробей

Чтобы сокращать дроби достаточно запомнить правило, которое состоит из двух шагов.

Правило сокращения дробей

Чтобы сократить дробь нужно:

1. Найти НОД числителя и знаменателя.
2. Разделить числитель и знаменатель на их НОД.

Рассмотрим практические примеры.

Пример 1. Сократим дробь.

Дана дробь 182 195 . Сократим ее.

Найдем НОД числителя и знаменателя. Для этого в данном случае удобнее всего воспользоваться алгоритмом Евклида.

195 = 182 · 1 + 13 182 = 13 · 14 Н О Д ( 182 , 195 ) = 13

Разделим числитель и знаменатель на 13 . Получим:

182 195 = 182 ÷ 13 195 ÷ 13 = 14 15

Готово. Мы получили несократимую дробь, которая равна исходной дроби.

Как еще можно сокращать дроби? В некоторых случаях удобно разложить числитель и знаменатель на простые множители, а потом из верхней и нижней частей дроби убрать все общие множители.

Пример 2. Сократим дробь

Дана дробь 360 2940 . Сократим ее.

Для этого представим исходную дробь в виде:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7

Избавимся от общих множителей в числителе и знаменателе, в результате чего получим:

360 2940 = 2 · 2 · 2 · 3 · 3 · 5 2 · 2 · 3 · 5 · 7 · 7 = 2 · 3 7 · 7 = 6 49

Наконец, рассмотрим еще один способ сокращения дробей. Это так называемое последовательное сокращение. С использованием этого способа сокращение производится в несколько этапов, на каждом из которых дробь сокращается на какой-то очевидный общий делитель.

Пример 3. Сократим дробь

Сократим дробь 2000 4400 .

Сразу видно, что числитель и знаменатель имеют общий множитель 100 . Сокращаем дробь на 100 и получаем:

2000 4400 = 2000 ÷ 100 4400 ÷ 100 = 20 44

Далее замечаем, что числитель и знаменатель дроби 20 44 делятся на 2 . Сокращаем и приходим к виду:

20 44 = 20 ÷ 2 44 ÷ 2 = 10 22

Получившийся результат снова сокращаем на 2 и получаем уже несократимую дробь:

Источник

Сокращение дробей. Что значит сократить дробь?

Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.

Сокращение дробей, определение и формула.

Что такое сокращение дробей? Что значит сократить дробь?

Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.

Формула сокращения дробей основного свойства рациональных чисел.

Рассмотрим пример:
Сократите дробь \(\frac<9><15>\)

Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.

Ответ: после сокращения получили дробь \(\frac<3><5>\). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.

Как сокращать дроби? Сокращение дроби до несократимого вида.

Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.

Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.

Получите несократимую дробь \(\frac<48><136>\).

Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6

Правило сокращения дроби до несократимого вида.

1. Нужно найти наибольший общий делитель для числители и знаменателя.
2. Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.

Пример:
Сократите дробь \(\frac<152><168>\).

Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6

Ответ: \(\frac<19><21>\) несократимая дробь.

Сокращение неправильной дроби.

Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.

Рассмотрим пример:
Сократите неправильную дробь \(\frac<44><32>\).

Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.

Сокращение смешанных дробей.

Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.

Рассмотрим пример:
Сократите смешанную дробь \(2\frac<30><45>\).

Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.

Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.

Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:

Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.

На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь \(\frac<100><150>\).

Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50

Получили несократимую дробь \(\frac<2><3>\).

Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь \(\frac<100><150>\) на 2.

Получили сократимую дробь \(\frac<50><75>\).

Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь \(\frac<4><8>\). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.

Пример:
Сравните две дроби \(\frac<2><3>\) и \(\frac<8><12>\).

Эти две дроби равны. Рассмотрим подробно дробь \(\frac<8><12>\):

Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.

Пример:
Сократите если возможно следующие дроби: а) \(\frac<90><65>\) б) \(\frac<27><63>\) в) \(\frac<17><100>\) г) \(\frac<100><250>\)

Источник

Сокращение обыкновенных дробей

В данной публикации мы рассмотрим правило сокращения обыкновенных дробей, которое изучается по школьной программе алгебры в 6-8 классах. Также разберем примеры решения задач для лучшего понимания и закрепления теоретического материала.

Сокращение дроби

Правило сокращения

Если и числитель, и знаменатель обыкновенной дроби имеют общий делитель, то их можно поделить на этот делитель, тем самым получив новую дробь, равную исходной. Эта действие называется сокращением дроби.

При этом, если числитель и знаменатель дроби взаимно просты, то она является несократимой.

Чтобы сократить дробь, выполняем следующие действия:

• раскладываем числитель и знаменатель на множители;
• зачеркиваем одинаковые числа, встречающиеся в обеих составных частях дроби;
• составляем новую дробь из оставшихся чисел.

Пример: сократим дробь 27 /₄₅.

Решение
В данном случае одним из множителей и числителя, и знаменателя является число 9, на которое и можно сократить дробь.

В сжатом виде сокращение обычно записывается так: числитель и знаменатель зачеркиваем, рядом с ними подписываем частные от их деления на общий делитель, который держим в уме, затем ставим знак равно и пишем получившуюся дробь.

Сокращение может выполняться поэтапно, т.е. делим дробь сначала на один общий делитель, затем – на другой.

Использование НОД

Чтобы за одно действие сразу максимально сократить дробь, требуется найти наибольший общий делитель (НОД) числителя и знаменателя. Затем остается только поделить составные части дроби на найденное значение.

Пример: давайте сократим дробь 564 /₂₄₄₈.

Решение
Разложим числитель и знаменатель на простые множители.

И обеих раскладках два раза встречается число 2 и один раз – число 3. Следовательно, НОД (564, 2448) = 2 ⋅ 2 ⋅ 3 = 12.

Таким образом, исходную дробь можно максимально сократить, разделив ее на 12.

Источник