Критерий гурвица является алгебраическим способом

Алгебраический критериЙ устойчивости Гурвица

Критерий основан на построении определителя, составленного из коэффициентов, входящих в характеристическое уравнение системы.

Запишем характеристическое уравнение для системы 6-го порядка в виде

. (7.11)

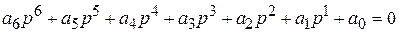
Аналогично можно записать уравнение системы любой степени, если порядок системы обозначить n. В нашем случае n=6.Уравнение записывается таким образом, чтобы коэффициент при высшей производной (а₆) был положительным, т.е. а₆ > 0.

Порядок построения определителя Гурвица.

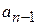
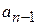
1. По главной диагонали записываются все коэффициенты от до а₀ включительно (=5).

2. Вверх по диагонали записываются коэффициенты уравнения в порядке убывания индексов, а вниз от диагонали – в порядке возрастания индексов.

3. На месте коэффициентов, не входящих в характеристическое уравнение, ставят нули.

4. Определители меньших порядков получают вычеркиванием последнего столбца и последней строки.

Условие устойчивости по Гурвицу

Система автоматического управления будет устойчивой, если все определители, составленные из коэффициентов характеристического уравнения системы, от D_n (D₆) до D₁ будут положительными, при этом а_n (а₆) должно быть больше нуля.

Построим определитель Гурвица для системы шестого порядка.

Если хотя бы один из определителей, называемых определителями Гурвица, отрицателен, система будет неустойчива.

Если главный определитель системы D_п=0, а все остальные определители положительны, то система находится на границе устойчивости.

Рассмотрим частные случаи критерия Гурвица для систем 1, 2, 3-го порядков. Раскрывая определители, фигурирующие в общей формулировке критерия, можно получить следующие условия.

1. Для уравнений первого порядка

,

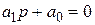
т.е. необходимым и достаточным условием устойчивости является положительность коэффициентов уравнения ( 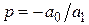0, D₁ = а₁ > 0; D₂ = а₀а₁ > 0.

Таким образом, и для системы второго порядка положительность коэффициентов является необходимым и достаточным условием устойчивости.

3. Для уравнений третьего порядка

,

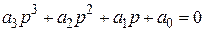
Последнее неравенство Δ₃ > 0 эквивалентно неравенству D₂ > 0. Следовательно, для системы третьего порядка кроме положительности всех коэффициентов уравнения требуется, чтобы D₂ > 0.

Критерий Гурвица применяют для анализа устойчивости систем не выше пятого порядка. При n > 5 вычисление определителей становится громоздким.

Источник

Алгебраический критерий устойчивости Гурвица

Для оценки устойчивости по этому критерию необходимо из коэффициентов характеристического уравнения составить определитель Гурвица по следующим правилам:

1) по главной диагонали выписываются все коэффициенты характеристического уравнения от а₁доа_nв порядке возрастания индексов;

2) столбцы определителя заполняются коэффициентами от главной диагонали вниз по убывающим, а вверх — по возрастающим индексам;

3) места коэффициентов, индексы которых больше nили меньше нуля заполняются нулями.

Пример.Составим определитель Гурвица, для системы 5-го порядка с характеристическим уравнением системы

,

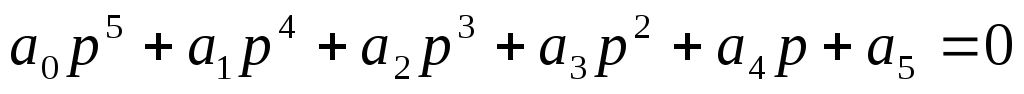
где все коэффициенты строго больше нуля. Получим

.

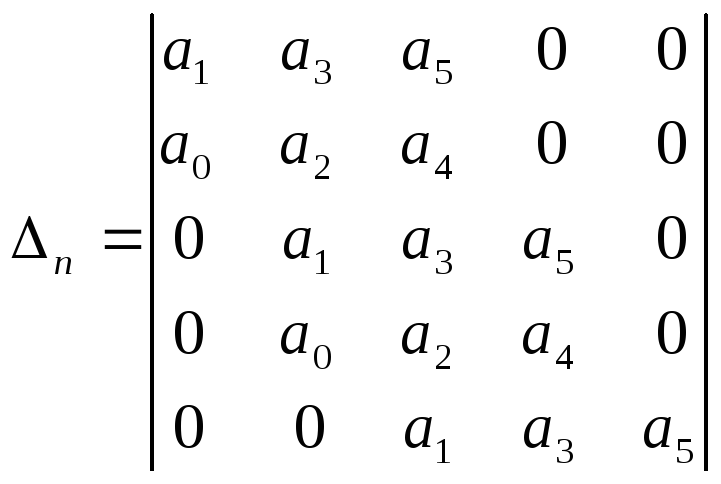
Для того чтобы все корни характеристического уравнения имели отрицательные вещественные части, и система была устойчивой необходимо и достаточно, чтобы все коэффициенты и все диагональные определители определителя Гурвица были строго больше нуля.

Для устойчивости системы 5-го порядка необходимо выполнение условий

Так как при выполнении необходимого условия устойчивости всегда а_n>0, то об устойчивости системы можно судить по определителям до_n-1включительно. Доказано, что если_n-1=0, то система находится на колебательной границе устойчивости, т.е. имеет пару чисто мнимых корней. Из условия_n-1=0можно определить критические значения параметров системы, при которых она выходит на границу устойчивости.

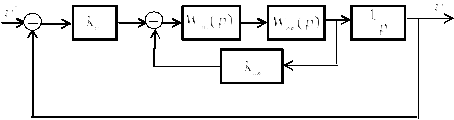
Пример.Исследовать устойчивость САУ. Система задана структурной схемой.

На схеме обозначено:

;;

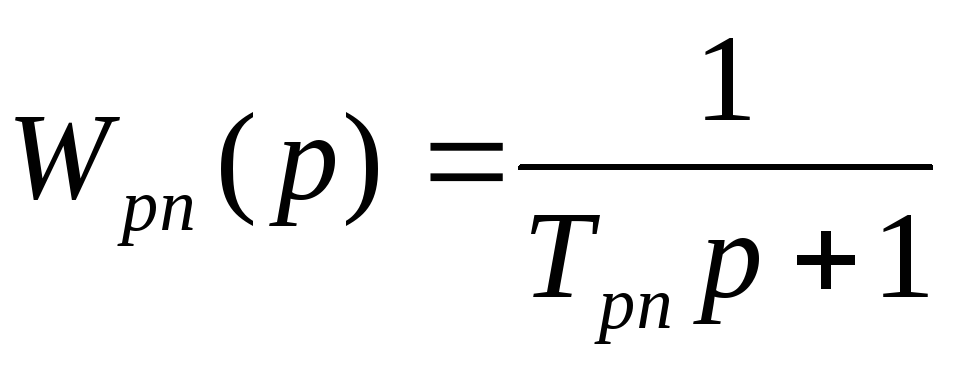
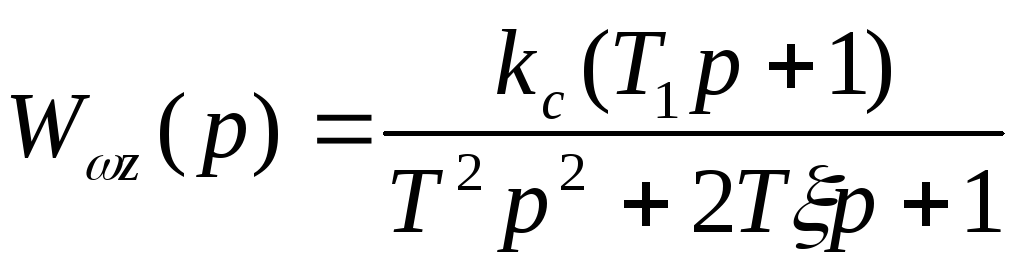
Для передаточной функции разомкнутой системы можно записать

,

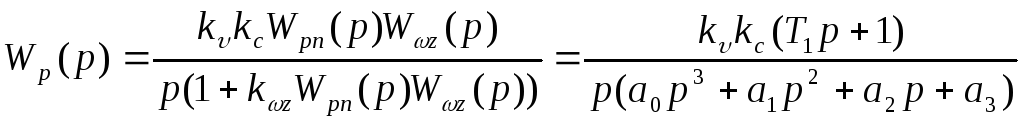
где ;;;.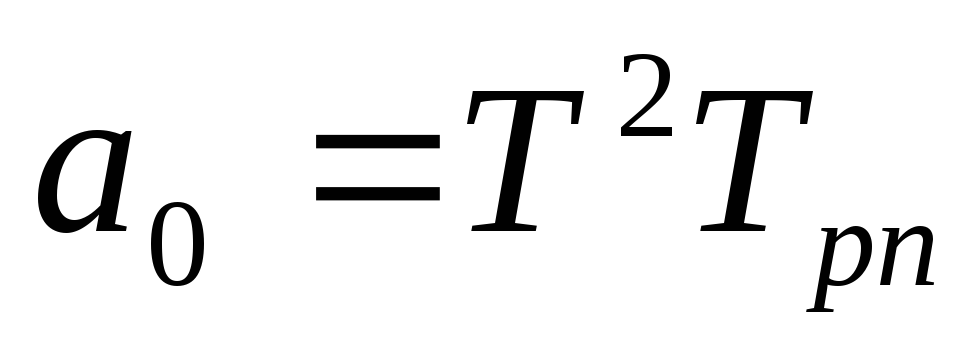

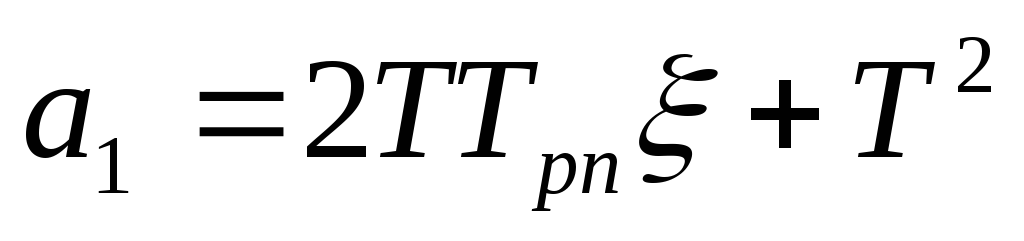
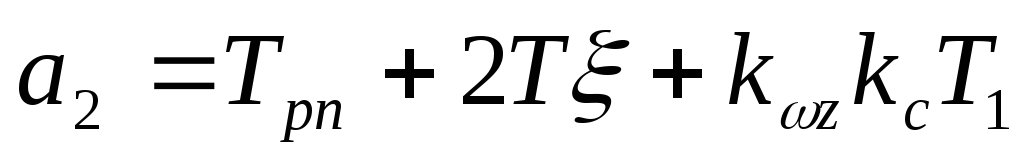
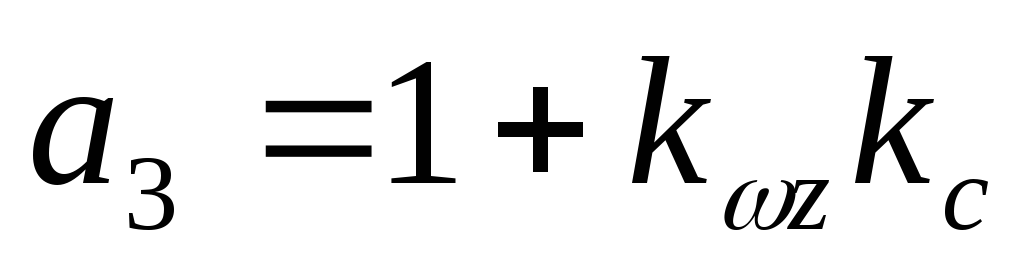
Передаточная функция замкнутой системы примет вид

,

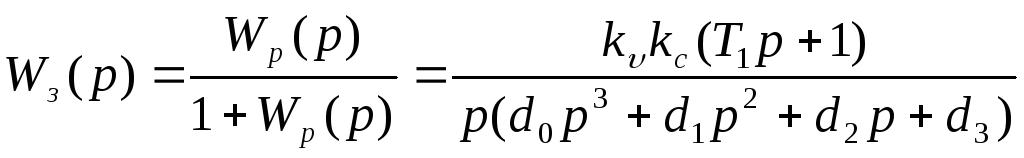
где ;;;;.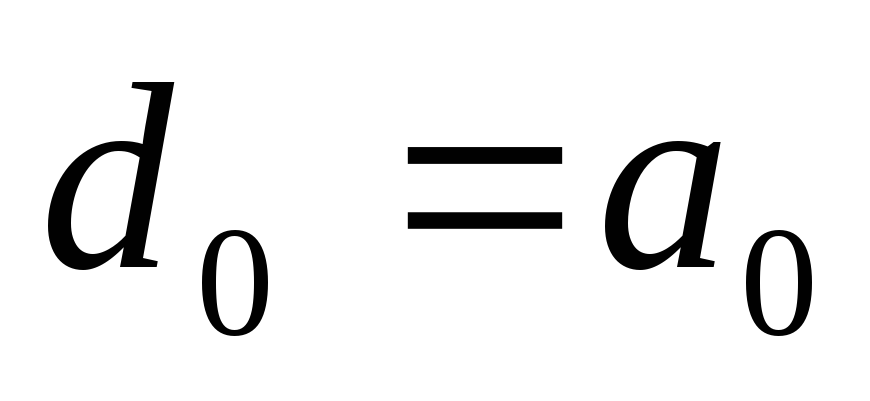

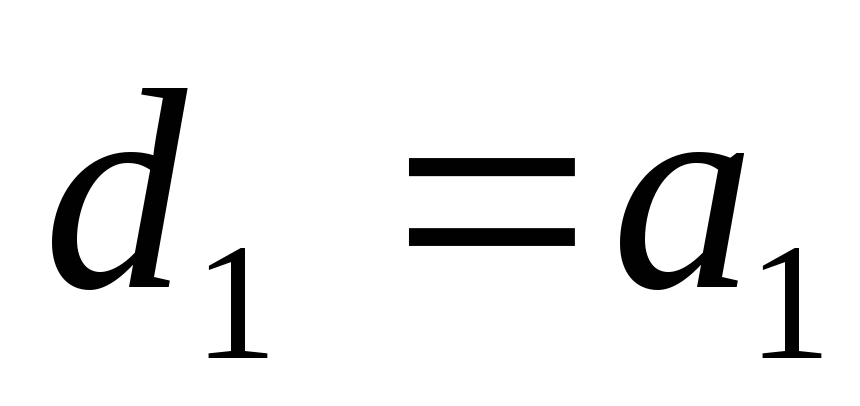
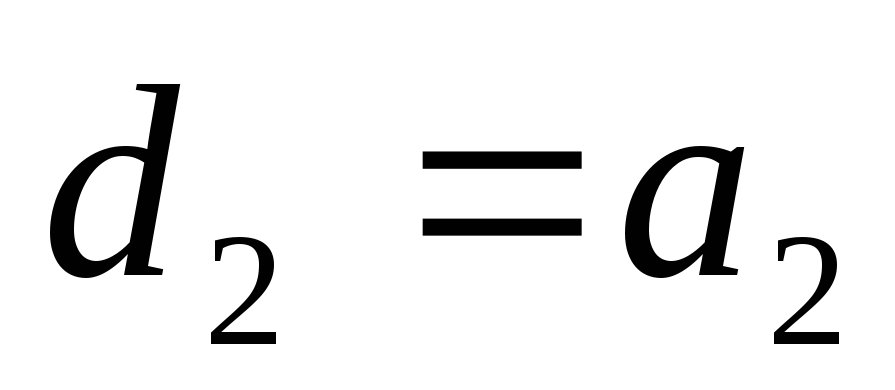
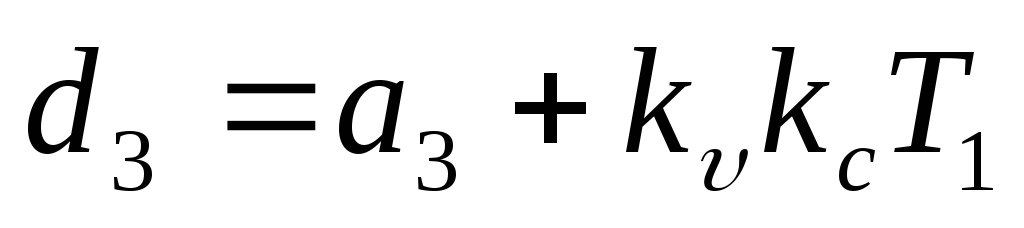
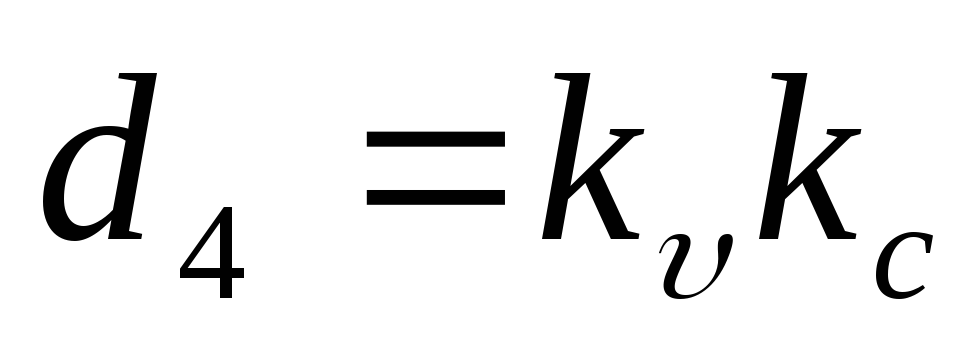
Составим определитель Гурвица

.

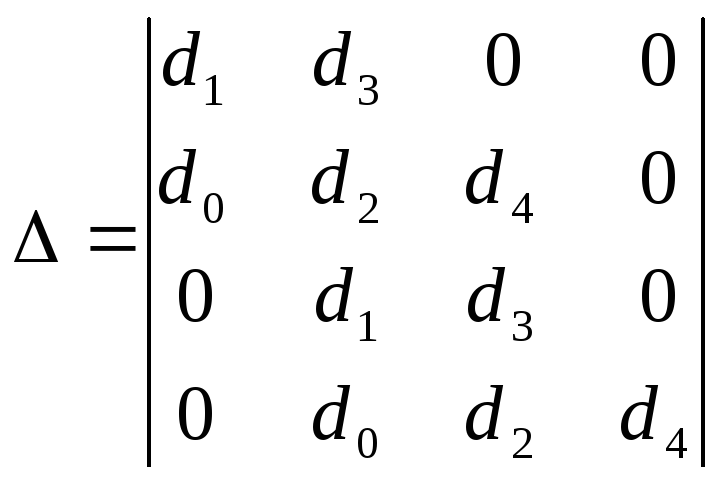
Оценим устойчивость системы для следующих значений параметров:

;;;,,;.

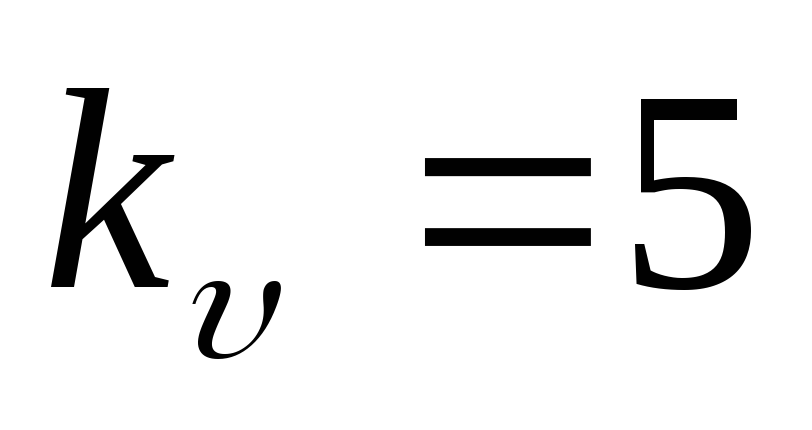
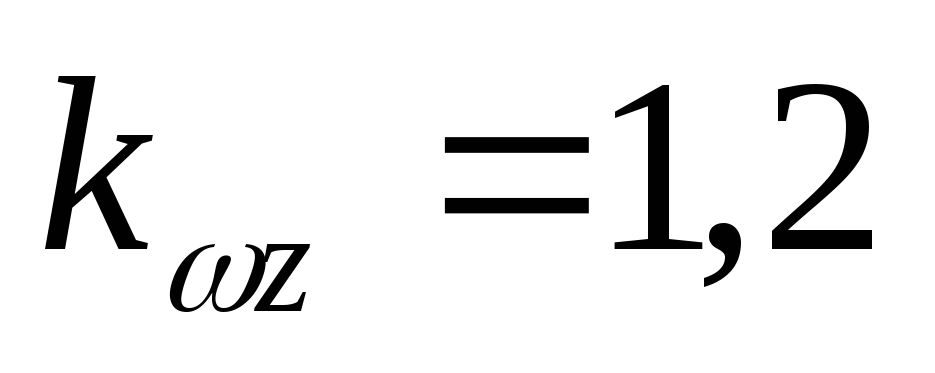
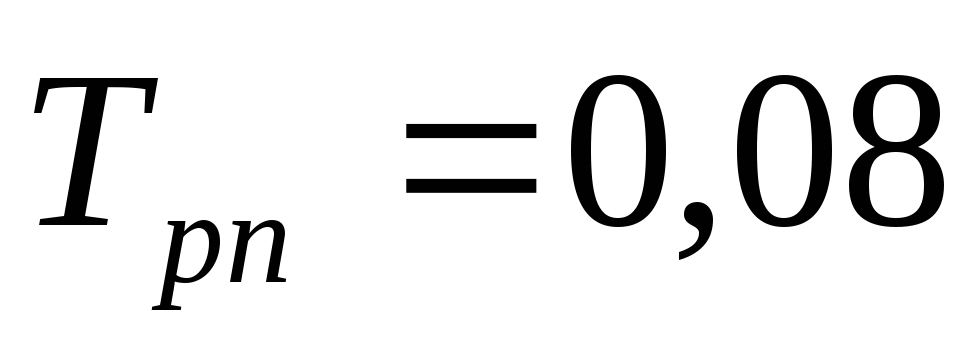
При этих значениях для коэффициентов характеристического уравнения получим

;;;;;.

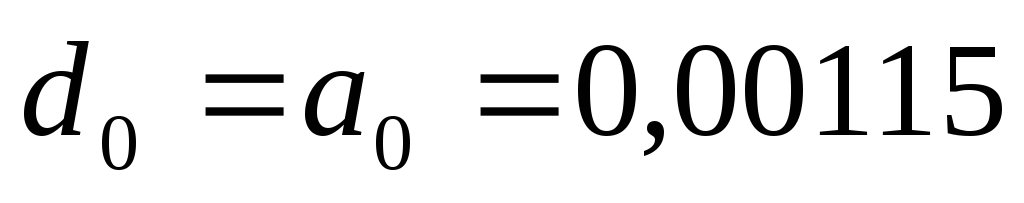
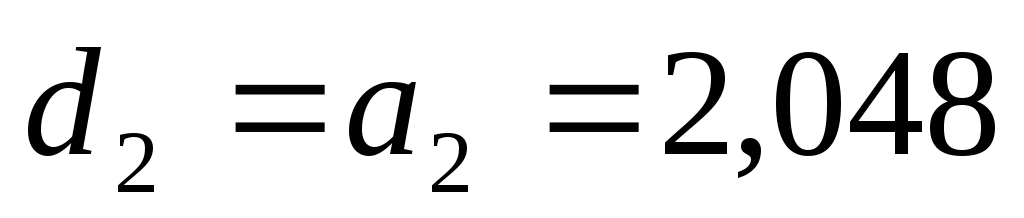
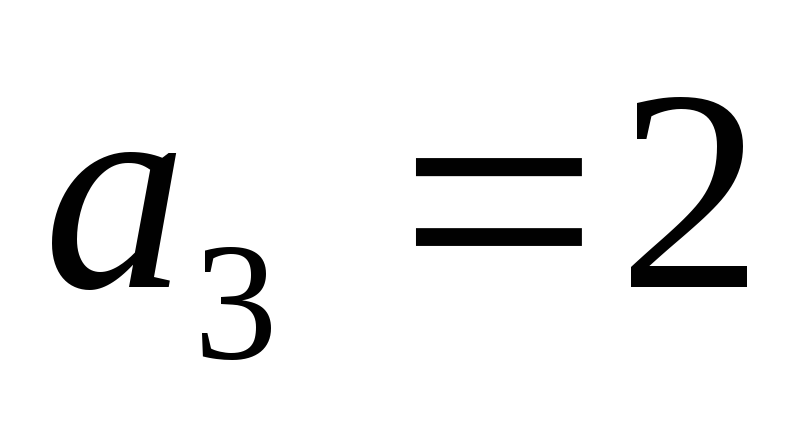
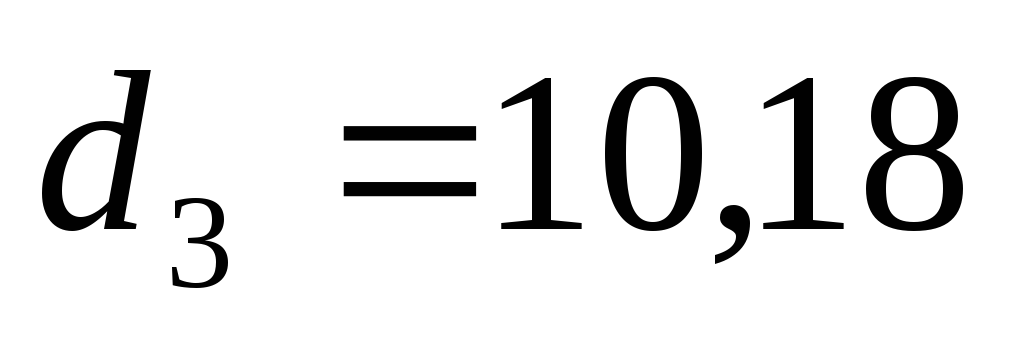
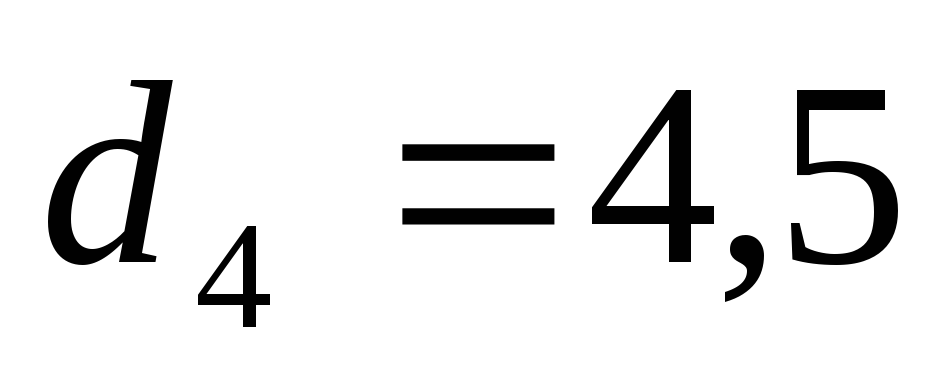
Следовательно, все коэффициенты характеристического уравнения замкнутой системы положительны и

;

;

.

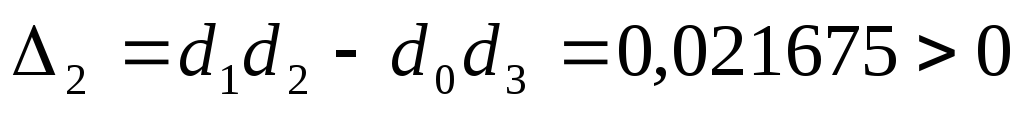
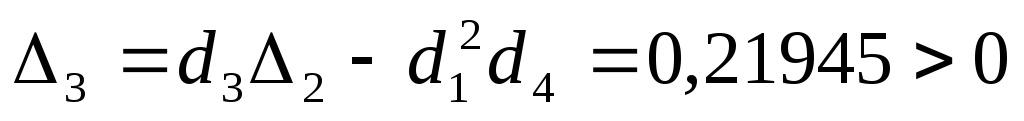
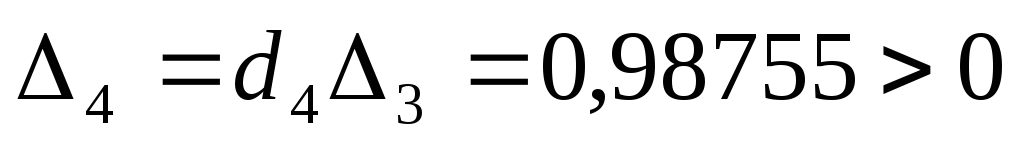
Условия устойчивости выполнены и система при избранных параметрах устойчива.

Частотные критерии устойчивости Принцип аргумента

Частотные критерии устойчивости используются в графоаналитическом виде и отличаются большой наглядностью при проведении расчетов. В основе всех частотных методов лежит принцип аргумента.

Рассмотрим характеристическое уравнение системы

.

.

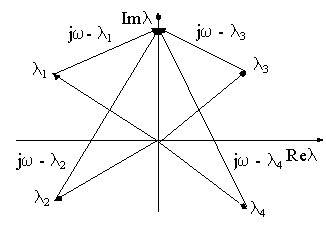
Каждому корню на комплексной плоскости соответствует определенная точка, и геометрически на этой плоскости каждый корень можно изобразить в виде вектора с модулем _i,проведенного из начала координат (рис.5.). Сделаем заменуp=j и получим

.

В соответствием с правилом вычитания векторов получим, что конец каждого элементарного вектора (j — _i)находиться на мнимой оси.

Рис. 5. К определению принципа аргумента

Аргумент вектора D(j) равен сумме аргументов элементарных векторов

.

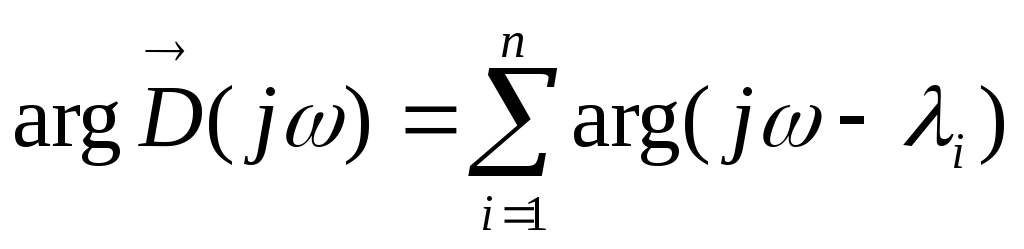
Направление вращения вектора (j — _i)против часовой стрелки при изменении частоты от— до +принято считать положительным, а по часовой стрелке — отрицательным. Предположим, что характеристическое уравнение имеетmкорней в правой полуплоскости и(n – m)корней в левой полуплоскости. При изменении частоты от— до + каждый вектор(j — _i),начало которого лежит в левой полуплоскости повернется на угол+, а каждый вектор, начало которого лежит в правой полуплоскости — на угол—. Изменение аргумента вектораD(j)при этом будет

. (6)

Это выражение и определяет принцип аргумента.

Источник

Критерий Гурвица

Назначение сервиса . С помощью онлайн калькулятора выбирается оптимальная стратегия по критерию Гурвица. Результаты вычислений оформляются в отчете формата Word (см. Пример оформления).

Пример . Исходные данные:

8	4	6	20
7	7	7	7
6	12	8	10

Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min a_ij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

Ai	П1	П2	П3	П4	min(aij)
A1	8	4	6	20	4
A2	7	7	7	7	7
A3	6	12	8	10	6

Выбираем из (4; 7; 6) максимальный элемент max=7
Вывод: выбираем стратегию N=2.
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max r_ij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r₁₁ = 8 — 8 = 0; r₂₁ = 8 — 7 = 1; r₃₁ = 8 — 6 = 2;
2. Рассчитываем 2-й столбец матрицы рисков.
r₁₂ = 12 — 4 = 8; r₂₂ = 12 — 7 = 5; r₃₂ = 12 — 12 = 0;
3. Рассчитываем 3-й столбец матрицы рисков.
r₁₃ = 8 — 6 = 2; r₂₃ = 8 — 7 = 1; r₃₃ = 8 — 8 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r₁₄ = 20 — 20 = 0; r₂₄ = 20 — 7 = 13; r₃₄ = 20 — 10 = 10

Ai	П1	П2	П3	П4
A1	0	8	2	0
A2	1	5	1	13
A3	2	0	0	10

Результаты вычислений оформим в виде таблицы.

Ai	П1	П2	П3	П4	max(aij)
A1	0	8	2	0	8
A2	1	5	1	13	13
A3	2	0	0	10	10

Выбираем из (8; 13; 10) минимальный элемент min=8
Вывод: выбираем стратегию N=1.
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма — оптимизма. За оптимальную принимается та стратегия, для которой выполняется соотношение:
max(s_i)
где s_i = y min(a_ij) + (1-y)max(a_ij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем s_i.
s₁ = 0.5•4+(1-0.5)•20 = 12
s₂ = 0.5•7+(1-0.5)•7 = 7
s₃ = 0.5•6+(1-0.5)•12 = 9

Ai	П1	П2	П3	П4	min(aij)	max(aij)	y min(aij) + (1-y)max(aij)
A1	8	4	6	20	4	20	12
A2	7	7	7	7	7	7	7
A3	6	12	8	10	6	12	9

Выбираем из (12; 7; 9) максимальный элемент max=12
Вывод: выбираем стратегию N=1.
Обобщенный критерий Гурвица.
Данный критерий является некоторым обобщением критериев крайнего пессимизма и крайнего оптимизма и также представляет собой частный случай обобщенного критерия Гурвица относительно выигрышей при следующем допущении:
λ₁=1-λ, λ2=λ3=…=λ_n-1=0, λ_n=λ, где 0 ≤ λ ≤ 1
Тогда показатель эффективности стратегии A_i по Гурвицу есть:
G_i=(1-λ)min a_ij + λmax a_ij
Оптимальной стратегией A_i0 считается стратегия с максимальным значением показателя эффективности.
Строим вспомогательную матрицу B, полученную путем упорядочивания показателей доходностей в каждой строке.
Подход пессимиста. λ выбирается из условия невозрастания среднего:

G₁ = 0.304 • 4+(1-0.304) • 20 = 15.143; G₂ = 0.304 • 7+(1-0.304) • 7 = 7; G₃ = 0.304 • 6+(1-0.304) • 12 = 10.179;
Подход оптимиста. λ выбирается из условия неубывания среднего:

G₁ = 0.696 • 4+(1-0.696) • 20 = 8.857; G₂ = 0.696 • 7+(1-0.696) • 7 = 7; G₃ = 0.696 • 6+(1-0.696) • 12 = 7.821

Ai	П1	П2	П3	П4	min(aij)	max(aij)	Подход пессимиста	Подход оптимиста
A1	4	6	8	20	4	20	15.14	8.86
A2	7	7	7	7	7	7	7	7
A3	6	8	10	12	6	12	10.18	7.82

Выбираем из (15.143; 7; 10.179) максимальный элемент max=15.14
Вывод: выбираем стратегию N=1.
Оптимальные стратегии по обобщенному критерию Гурвица.
b = 17 + 21 + 25 + 39 = 102
Показатели эффективности по Гурвицу.
Подход пессимиста



Подход оптимиста

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₁.

Источник