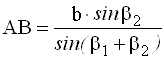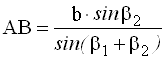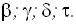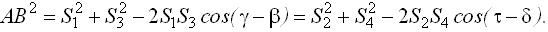Косвенный способ определения расстояния между точками это когда

Ekzamen_geodezia (1) / 27.Определение недоступных расстояний между двумя взаимно видимыми и невидимыми точками

27. Косвенные измерения длин линий

При измерении расстояний лентой или рулеткой встречаются случаи, когда местное препятствие (река, овраг, здание, дорога и т.п.) делает непосредственное измерение невозможным. Тогда применяют косвенные методы определения расстояний.

Различают три случая определения недоступных расстояний.

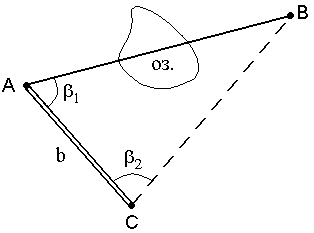
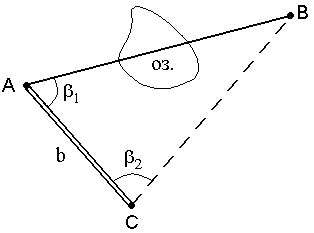
1. При взаимной видимости точек разбивают базис b и измеряют горизонтальные углы и

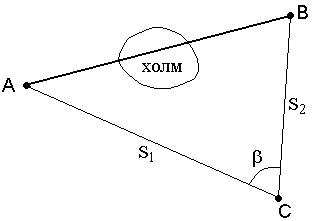
Рис. 51. Косвенное измерение расстояния через озеро

Для определения расстояния АВ используют теорему синусов

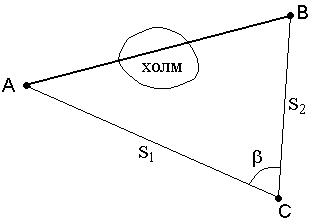
2. При взаимной невидимости точек (рис. 52) выбирают точку С из которой видны точки А и В, измеряют расстояния S₁, S₂ и угол .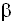

Рис. 52. Косвенное измерение расстояния через

Используя теорему косинусов, находят расстояние АВ

.

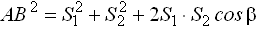
Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Источник

Косвенные измерения длин линий

При измерении расстояний лентой или рулеткой встречаются случаи, когда местное препятствие (река, овраг, здание, дорога и т.п.) делает непосредственное измерение невозможным. Тогда применяют косвенные методы определения расстояний.

Различают три случая определения недоступных расстояний.

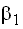
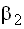
1. При взаимной видимости точек разбивают базис b и измеряют горизонтальные углы и (рис. 51).

Рис. 51. Косвенное измерение расстояния через озеро

Для определения расстояния АВ используют теорему синусов

2. При взаимной невидимости точек (рис. 52) выбирают точку С из которой видны точки А и В, измеряют расстояния S₁, S₂ и угол .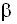

Рис. 52. Косвенное измерение расстояния через

Используя теорему косинусов, находят расстояние АВ

.

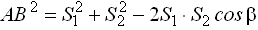
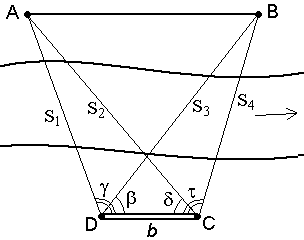
3. Если обе точки измеряемого расстояния недоступны, то разбивают базис b и из точек С и Д измеряют углы

Рис. 53. Косвенное измерение расстояний если недоступны обе точки

По теореме синусов дважды для контроля находят с контролем расстояние АВ.

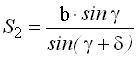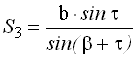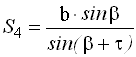Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Источник

Косвенные способы измерения расстояний

Рисунок 24 — Схема измерения линии на наклонном участке

Рисунок 23 — Принцип измерения расстояния оптическим дальномером

Для измерения линии на одном конце устанавливают прибор, а на другом рейку.

Пусть визирная ось трубы горизонтальна. Из подобия треугольников

AFB и a’Fb’ следует, что OF/AB=OF/a’b’. Введём обозначения: AB=n; 0F=D’; FO=f; a’b’=P, то:

D’/n=f/n,откуда D’=f/P . n,

где f – фокусное расстояние объектива;

P – расстояние между дальномерными нитями;

n – расстояние между нитями по рейке;

D’ – расстояние от рейки до переднего фокуса объектива F.

Отношение f/P для данного прибора величина постоянная и называется коэффициентом дальномера, её обозначают буквой «К», то есть f/P=K. Поэтому:

D’ = K . n (14)

На рисунке видно, что для получения расстояния от оси прибора до рейки необходимо прибавить фокусное расстояние f и расстояние от объектива до оси вращения трубы δ.

Таким образом: d = D + f + δ.

Расстояние f + δ обозначают C =f + δ и называют постоянным слагаемым дальномера. Для определения искомого расстояния имеем:

D = K . n + C (15)

В современных приборах постоянное слагаемое мало и его часто не учитывают, тогда предыдущая формула имеет вид:

D = K . n (16)

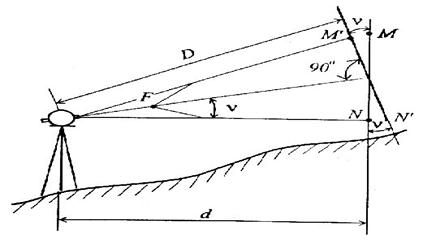
Это рабочая формула дальномера и так как К = 100, то упрощается вычисление. Полученная формула верна для случая, когда рейка расположена перпендикулярно к визирной оси трубы. При измерениях на местности это условие нарушается, так как при наклонном положении визирной оси рейку устанавливают вертикально (рисунок 24).

Если рейка наклонена по отношении к визирной оси на угол v, то вместо правильного отсчёта M’N’=m возьмут отсчёт MN=n. Эти величины связаны соотношением n’=n . cos v, но так как d=D . cos v, то:

d = K . n . cos v. (17)

На практике встречаются случаи, когда для измерения линий невозможно использовать ленту из-за препятствий (река, болото, овраг, лес и т.д.). Наиболее часто встречающийся случай определения недоступного расстояния показан на рисунке 25 а.

Источник

Косвенный способ определения расстояния между точками это когда

Л. 7 ЛИНЕЙНЫЕ ИЗМЕРЕНИЯ

При любой съемке выполняют линейные измерения. Расстояние можно измерить непосредственно уложением прибора в створ, с помощью дальномеров и косвенно. Соответственно различают непосредственные измерения, дальномерные и косвенные.

Применение определенного способа измерений зависит от вида съемки, требуемой точности измерений и наличия приборов.

1. Непосредственные измерения

Для непосредственного измерения используют стальные землемерные ленты, рулетки, инварные ленты и проволоки.

Инвар — сплав железа и никеля ( 64% и 36 %), обладающий незначительным коэффициентом теплового расширения и поэтому мерные приборы из него при соответствующем натяжении в 10 кг позволяют определять расстояния с высокой точностью. Относительная погрешность измерений инварными приборами 1/25 000 — 1/ 100 000. Самые распространенные стальные ленты : землемерная штриховая ЛЗ — 20 и лента землемерная шкаловая ЛЗШ – 20 с номинальным расстоянием между крайними штрихами 20 м. Наименьшее деление на ленте штриховой – дециметр (10 см). При снятии отсчета по ленте сантиметры оцениваются на глаз. На ЛЗШ – 20 на концах ленты закреплены шкалы длиной 10 см с миллиметровыми делениями. Погрешность отсчета по шкале 0,5 мм. Применяется при измерениях с повышенной точностью. Рулетки производятся с различным номиналом длины – 10,20,30,50 м с нанесенными сантиметровыми делениями. В некоторых рулетках конечные дециметровые деления разделены на миллиметры. Стальные ленты и рулетки дают относительную погрешность 1/ 1000 – 1/ 5000. При непосредственных измерениях ленту (рулетку) последовательно укладывают в створе измеряемой линии , считают количество уложений прибора n и в конце отрезка измеряют остаток ro : Do = lo n +ro . Укладка в створ линии производится по теодолиту или на глаз.

Для обеспечения видимости на конечных точках устанавливаю вешки , раскрашенные полосками красного и белого цвета. Если длина линии более 150 м , то ее необходимо провешить. Вешение – установка вешек в створе линии, то есть в вертикальной плоскости, проходящей через ее конечные точки.

Чтобы не закрывать видимость по створу, вешение производят «на себя», то есть начинают с точки 1, затем устанавливают вешку в точке 2 и т.д. Рисунок:

Фиксация концов ленты на земле производится металл. шпильками. Для приведения измеряемой линии к горизонту, то есть для вычисления горизонтального проложения, измеряют угол наклона измеряемых линий теодолитом либо эклиметром или измеряют превышение между точками нивелиром. При оценке углов наклона небольших отрезков на местности (10 – 50 м) можно применить простой портативный прибор – эклиметр. Например, ЭВ-1 (эклиметр-высотомер), позволяющий измерять углы наклона и высоты объектов в ходе геологич-х и геодезических изысканий. В корпусе эклиметра помещен вертикальный круг (лимб), работающий по принципу маятника. По краю лимба нанесены две шкалы. Одна — для определения угла наклона в градусах, другая — для определения высот в метрах, рассчитанная на две дистанции 15 и 20 м, то есть на два расстояния от наблюдателя. Отсчет производят через визирную лупу в корпусе прибора. Визирный индекс наводят на объект , нажимают кнопку и после успокоения лимба снимают отсчет. Цена деления – 1˚, но можно на глаз оценить и десятые доли градуса. В этом приборе нет зрительной трубы, увеличения нет, потому и применяется на небольших расстояниях для приблизительной оценки вертикальных углов.

При измерении наблюдатель с эклиметром стоит в начальной точке, а в конце линии на местности – помощник с вехой. На вехе нанесена метка на уровне глаз наблюдателя, на которую наводится визирный штрих (индекс) эклиметра. i

i ν

Точность эклиметра достаточна для определения угла наклона при приведении измеренной линии к горизонту.

Фактическая длина мерного прибора по разным причинам может отличаться от номинала на несколько миллиметров или даже сантиметров и изменяется с изменением температуры. Поэтому если измерения требуют достаточно высокой точности , необходимо выполнить компарирование , то есть определить фактическую длину прибора при температуре измерения ( данной температуре воздуха).

Компарирование — сравнение с эталоном, то есть с мерным прибором, длина которого известна с высокой точностью. В качестве эталона можно использовать специальный штриховой метр с ценой деления 0,2 мм, который последовательно укладывают вдоль натянутой ленты. Может сравнивать с эталонной лентой или рулеткой, длина которых соответствует номиналу. Можно также использовать полевой компаратор (обычно длиной 120 м), длина которого определена с высокой точностью – например, светодальномером. Длина полевого компаратора Dк измеряется многократно и вычисляется среднее значение Dфакт. Поправка «за компарирование» в длину ленты или рулетки: Δlк = lфакт — lo или Δlк = (Dфакт — Dк) / n , где n — число уложений в створе рабочего мерного прибора. При компарировании измеряют температуру воздуха tо˚ , чтобы учесть поправку «за температуру». Е находят с учетом коэффициента теплового расширения стали. Эта поправка не учитывается, если разность температур при измерении и при компарировании не превышает 8˚. Для приведения длины линии к горизонту измеряют угол наклона или превышение. Таким образом, для вычисления горизонтального проложения d измеренного отрезка с длиной по номиналу D о нужно ввести три поправки:

d = Dо + ΔDк + ΔDt — ΔDν

Здесь Do — длина линии по номиналу прибора; ΔDк = (Dо / lo) Δlк ;

lo — длина прибора по номиналу; ΔDt = Do * α * (t˚ — to˚) ; где t˚- температура во время измерения, α = – коэффициент теплового расширения стали.

ΔDν = D — d — поправка «за угол наклона».

d = D * cos ν ; ΔDν = D — D*cos ν = D*(1-cos ν ) = 2Dsin²ν/2

Если определялось превышение, то поправку эту можно рассчитать по формуле: ΔDh = h² / (2*D). Этой поправкой можно пренебречь, если угол наклона не превышает 1.5˚ . Для контроля измерений и повышения точности длины линий измеряют в прямом и обратном направлениях. Расхождение между двумя измерениями: ΔD = Dпр — Dобр не должно превышать заданной нормативной точности в соответствии с нормами и правилами производства работ.

(нормативная точность) 1 /N = 1/1000 ; 1/1500; 1/ 2000; 1/3000; 1/5000.

При допустимости вычисляют среднее, которое принимают за результат измерения: Dср = (Dпр + Dобр ) / 2 Например, Dпр= 200,25 Dобр= 200,45 м ; 1/N = 1/2000 — благопр. условия измерений.

ΔD = 0.20м Dср = 200.35 м Δ D/ Dср = 0.20 / 200.35 = 1/ 1000 .

Вывод: Измерение выполнено неточно для данных условий.

2. Дальномерные измерения

Для дальномерных измерений расстояний используются оптические дальномеры, либо электронные геодезические инструменты с электронными дальномерами.

О птические дальномеры

Определение расстояний этими дальномерами основано на решении равнобедренного треугольника, в котором искомое расстояние D определяется по малому углу β , который называют параллактическим, и по противолежащей стороне b , называемой базой.

Эти три величины связаны между собой формулой: D = b/2 * ctg β / 2 . При определении расстояний одна из величин — угол или база принимается постоянной, а вторую измеряют. В зависимости от этого различают :

1) дальномеры с переменным углом и постоянной базой;

2) дальномеры с постоянным углом и переменной базой.

Первый тип оптических дальномеров с постоянной базой представляет собой оптическое устройство, которое закрепляется на зрительной трубе прибора со стороны объектива. В комплект входит также постоянный базис обычно длиной 1 м , который устанавливается горизонтально на штативе и центрируется над удаленной точкой. Дальномерные насадки имеют микроскопы, позволяющие с высокой точностью измерять углы β /2 и соответственно расстояния до 700 м. В настоящее время эти дальномеры практически не используют, их заменили электронные дальномеры.

Что касается второго типа оптических дальномером – с постоянным параллактическим углом, то он широко применяется в виде нитяного дальномера.

Нитяной дальномер с постоянным параллактическим углом имеется в зрительных трубах геодезических приборов (в теодолитах и нивелирах) и состоит он из двух горизонтальных штрихов, расположенных симметрично относительно центрального горизонтального штриха (нити). Эти штрихи называются дальномерными нитями. Визирные нити в различных приборах могут выглядеть так:

В комплект нитяного дальномера входит дальномерная рейка с делениями.

Принципиальная схема нитяного дальномера :

ось вращения прибора

M — место установки прибора; N — место установки рейки.

Искомое расстояние : D = D‘ + f + δ .

Из подобия треугольников AFB и aFb следует: D‘ / n = f / p D‘ = f/p *n. Отношение f / p = K называется коэффициентом дальномера, который постоянен для данного прибора.

f + δ = c — постоянное слагаемое дальномера. После подстановки в формулу для расстояния D получим: D = K * n + c. В современных приборах с внутренней фокусировкой c = 0. D = K * n

Для удобства расчетов нитяной дальномер рассчитывают так, что K = 100 .

В этом случае 1 см на рейке соответствует 1 м на местности. Если разность отсчетов взять в см, то сразу получим расстояние в метрах. Например, отсчет а = 1655 , b = 1500. Тогда n = 155 мм = 15,5 см.

d = K * n = 100 *155 = 15500 мм = 15,5 м.

При определении расстояний по этой формуле предполагается, что дальномерная рейка перпендикулярна линии визирования. Однако, при определении наклонных расстояний, очевидно, что линия визирования не будет перпендикулярна к вертикально стоящей рейке. Рисунок:

Для вычисления действительного расстояния D необходимо от отсчета по рейке n перейти к отсчету n‘ , который соответствует правильному положению рейки. В верхнем маленьком треугольнике угол при вершине C равен углу наклона линии визирования ν , а угол при точке В близок к 90˚. Поэтому можно записать:

n’ / 2 = n / 2 * cos ν или n’ = n * cos ν .

В формуле для D нужно заменить n на n’ . Тогда

D = K * n * cos ν , а горизонтальная проекция линии будет равна:

d = D * cos ν = K * n * cos²ν

Точность определения расстояний нитяным дальномером характеризуется относительной погрешностью в среднем около 1 / 400 , а в общем погрешность в пределах 1/200 — 1/500. Точность невысока. Поэтому оценка расстояний достаточно приблизительна. Так, для неблагоприятных условий съемки берем 1/ 200, то есть с абсолютной ошибкой в 1 м на каждые 200 м. Тем не менее, для решения некоторых задач эта точность вполне приемлема. Рекомендуется для измерения относительно коротких линий до 100 – 200 м.

Электронные дальномеры

К дальномерам этого типа относят радио – и светодальномеры. Они бывают импульсные и непрерывного излучения ( фазовые); с уголковым или пассивным отражателем ( светодальномеры) и активным отражателем ( радиодальномеры).

Уголковые призменные отражатели отражают падающий на них свет строго в обратном направлении независимо от их разворота. В основе всех электронных средств измерений расстояния D лежит известная из курса физики формула: D = ( ½) * v * t , где t — время распространения э/м колебаний вдоль измеряемой линии и обратно; v = c / n – скорость распространения в воздухе э/м волн; с — то же в вакууме, равно 300 000 км/с ; n — коэффициент преломления в атмосфере, равный 1,00028 – 1,00035.

На одном конце линии устанавливается приемо-передающее устройство. На другом конце – отражатель. Если измерить время прохождения э/м волн до отражателя и обратно, то можно рассчитать искомую длину.

Это время может быть измерено прямым и косвенным методами.

Непосредственное прямое определение промежутка времени t реализуется в импульсных дальномерах. При этом время соответствует прохождению электромагнитного импульса до отражателя и обратно. Ясно, что при этом должны быть использованы высокоточные электронные счетчики, способные фиксировать столь малые промежутки времени.

Косвенный метод основан на измерении разности фаз исходного и принятого колебаний. Разность фаз является функцией временного интервала. Такие дальномеры называются фазовыми. Фазовый метод является наиболее точным при измерении расстояний.

Р адиодальномеры с активным отражателем являются фазовыми, а слово «активный » означает , что радиосигнал не просто отражается, а трансформируется и излучение идет обратно с другой частотой . Такой радиодальномер состоит из двух взаимозаменяемых станций – ведущей и ведомой. Ведущая излучает колебания с частотой f ( сантиметровые длины волн). Ведомая принимает сигнал, трансформирует в другое излучение с частотой f . Расчет ведется по этой же формуле. Радиодальномеры используются для измерения больших расстояний и в навигации – например при съемке с летательных аппаратов. Светодальномеры используют оптический световой диапазон э/м излучений и используются довольно часто для выполнения инженерно-геодезических измерений. Существуют светодальномеры, не требующие в работе отражателя . Это светодальномеры с пассивным отражением – они используют отражательные свойства самих предметов , на которые визируется прибор. Нужно отметить не только высокую точность измерения, но и возможность использования прибора в любое время суток и независимо от сезона года . Как правило, используется видимый лазерный луч света – концентрированный пучок света с очень низким рассеянием. Светодальномеры бывают разной дальности действия . Определение расстояний до 50 км с ошибкой в несколько мм на каждый километр ведется приборами первой группы с буквой Г, используются при создании плановых геодезических сетей. Ко второй группе с буквой Т относят светодальномеры малой дальности — топографические до расстояний в несколько км — для производства топосъемок. Светодальномеры третьей группы с буквой П измеряют расстояния от 100 м до 3 км и используются в прикладной геодезии , в частности при строительстве и эксплуатации сооружений.

3. Косвенные способы измерения расстояний (определение недоступного расстояния)

Эти способы применяются, если между начальной и конечной точками измеряемой линии на местности имеются препятствия река, овраг, лес и т.д.), что не позволяет выполнить непосредственные измерения, а иногда и дальномерные. Как правило, применяется одна из расчетных схем, о которых пойдет речь. В основе трех из четырех способов лежат тригонометрические формулы решения треугольников.

1. Параллактический способ

Пусть требуется определить Х – расстояние от точки D до точки В , которые разделены оврагом. Перпендикулярно к линии BD на местности закрепляют базис АС, который измеряют максимально точными приборами, имеющимися в наличии. Тщательно измеряют теодолитом угол при точке В — параллактический угол (угол, опирающийся на известную сторону в треугольнике). При таком построении расстояние вычисляют по формуле:

Схема определения расстояния параллактическим способом

В

Х = ½ * b * ctg β /2 β

А D C

б а з и с b

Относительная погрешность 1/2000 будет обеспечена, если угол β измерен точным теодолитом , сам угол не будет меньше 12˚ , а базис — инварными проволоками или светодальномерами.

2. Применение теоремы синусов

В данном примере препятствие м является река . Расстояние определяют по измеренным на местности базису b1 и двум горизонтальным углам α1 и β1 , измеренным теодолитом. Если есть возможность, для контроля измеряется и третий угол γ .

Из теоремы синусов – отношение сторон в треугольнике равно отношению синусов противолежащих углов.

Х1 / b1 = sin β1 / sin γ1 В

Х1 = b1* sin β1 / sin γ1 = &nbs… Продолжение »

Источник