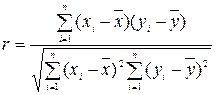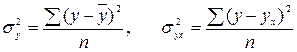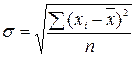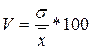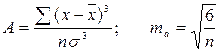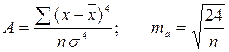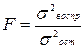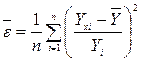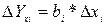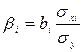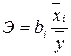Стохастический факторный анализ
Стохастическое моделирование факторных систем взаимосвязей отдельных сторон хозяйственной деятельности строится на обобщении закономерностей варьирования значений экономических показателей – количественных характеристик факторов и результатов хозяйственной деятельности. Количественные параметры связи выявляются на основе сопоставления значений изучаемых показателей в совокупности хозяйственных объектов или периодов.
Стохастическая (вероятностная) связь – связь, при которой каждому значению факторного признака соответствует множество значений результативного признака.
Таким образом, первой предпосылкой стохастического моделирования является возможность составить совокупность наблюдений, т. е. возможность повторно измерить параметры одного и того же явления в различных условиях.
В стохастическом анализе, где сама модель составляется на основе совокупности эмпирических данных, предпосылкой получения реальной модели является совпадение количественных характеристик связей в разрезе всех исходных наблюдений. Это означает, что варьирование значений показателей должно происходить в пределах однозначной определенности качественной стороны явлений, характеристиками которых являются моделируемые экономические показатели (в пределах варьирования не должно происходить качественного скачка в характере отражаемого явления).
Значит, второй предпосылкой применяемости стохастического подхода моделирования связей является качественная однородность совокупности (относительно изучаемых связей).
Изучаемая закономерность изменения экономических показателей (моделируемая связь) выступает в скрытом виде. Она переплетается со случайными с точки зрения исследования (не изучаемыми) компонентами вариации и ковариации показателей. Закон больших чисел гласит, что только в большой совокупности закономерная связь выступает устойчивее случайного совпадения направления варьирования (случайной вариации).
Из этого вытекает третья предпосылка стохастического анализа – достаточная размерность (численность) совокупности наблюдений» позволяющая с достаточной надежностью и точностью выявить изучаемые закономерности (моделируемые связи).
Четвертая предпосылка стохастического подхода – наличие методов, позволяющих выявить количественные параметры экономических показателей из массовых данных варьирования уровня показателей. Математический аппарат применяемых методов иногда предъявляет специфические требования к моделируемому эмпирическому материалу. Выполнение данных требований является важной предпосылкой применяемости методов и достоверности полученных результатов.
Основная особенность стохастического факторного анализа заключается в том, что при стохастическом анализе нельзя составлять модель путем качественного (теоретического) анализа, необходим количественный анализ эмпирических данных.
Методы стохастического факторного анализа
Способ парной корреляции. Метод корреляционного и регрессионного (стохастического) анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости, т.е. связь, проявляется не в каждом отдельном случае, а в определенной зависимости. С помощью парной корреляции решаются две главные задачи: оставляется модель действующих факторов (уравнение регрессии); дается количественная оценка тесноты связей (коэффициент корреляции).
Матричные модели. Матричные модели представляют собой схематическое отражение экономического явления или процесса с помощью научной абстракции. Наибольшее распространение здесь получил метод анализа «затраты-выпуск», строящийся по шахматной схеме и позволяющий в наиболее компактной форме представить взаимосвязь затрат и результатов производства.
Математическое программирование – это основное средство решения задач по оптимизации производственно-хозяйственной деятельности.
Метод исследования операций направлен на изучение экономических систем, в том числе производственно-хозяйственной деятельности предприятий, с целью определения такого сочетания структурных взаимосвязанных элементов систем, которое в наибольшей степени позволит определить наилучший экономический показатель из ряда возможных.
Теория игр как раздел исследования операций — это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы.
Литература:
- Баканов М. И., Мельник М. В., Шеремет А. Д. Теория экономического анализа. Учебник 5-еизд., перераб. и доп.-М.: Финансы и статистика,2005
- Фролова Т.А. Анализ и диагностика финансово-хозяйственной деятельности предприятия. Конспект лекций, Таганрог: ТРТУ, 2006
Источник
Тема 5. Методы стохастического факторного анализа
5.1. Способ парной корреляции
Метод корреляционного и регрессионного (стохастического) анализа широко используется для определения тесноты связи между показателями, не находящимися в функциональной зависимости, т.е. связь проявляется не в каждом отдельном случае, а в определенной зависимости.
С помощью корреляции решаются две главные задачи:
- составляется модель действующих факторов (уравнение регрессии);
- дается количественная оценка тесноты связей (коэффициент корреляции).
5.3. Матричные модели
Матричные модели представляют собой схематическое отражение экономического явления или процесса с помощью научной абстракции. Наибольшее распространение здесь получил метод анализа «затраты-выпуск», строящийся по шахматной схеме и позволяющий в наиболее компактной форме представить взаимосвязь затрат и результатов производства.
5.4. Математическое программирование
Математическое программирование — это основное средство решения задач по оптимизации производственно-хозяйственной деятельности.
5.5. Метод исследования операций
Метод исследования операций направлен на изучение экономических систем, в том числе производственно-хозяйственной деятельности предприятий, с целью определения такого сочетания структурных взаимосвязанных элементов систем, которое в наибольшей степени позволит определить наилучший экономический показатель из ряда возможных.
5.6. Теория игр
Теория игр как раздел исследования операций — это теория математических моделей принятия оптимальных решений в условиях неопределенности или конфликта нескольких сторон, имеющих различные интересы.
Бальжинов А.В., Михеева Е.В. Анализ и диагностика финансово-хозяйственной деятельности предприятия: Учебн.пособ., — Улан-Удэ, 2003.
Источник
Стохастический анализ



Стохастический анализ представляет собой методику исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной, вероятностной (корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель.
Корреляционная (стохастическая) связь – это неполная, вероятностная зависимость между показателями, которая проявляется только в массе наблюдений. Отличают парную и множественную корреляцию.
Парная корреляция – это связь между двумя показателями, один из которых является факторным, а второй – результативным.
Множественная корреляция – возникает от взаимодействия нескольких факторов с результативным показателем.
Необходимые условия применения корреляционного анализа:
1. Наличие большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов).
2. Исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.
Применение корреляционного анализа позволяет решить следующие задачи:
— определить изменение результативного показателя под воздействием одного или несколько факторов, т.е. определить насколько единиц изменяется величина результативного показателя при изменении факторного на единицу;
— установить относительную степень зависимости результативного показателя от каждого фактора.
Корреляционный анализ – метод установления связи и измерения ее тесноты между наблюдениями, которые можно считать случайными и выбранными из совокупности, распределенной по многомерному нормальному закону.
Корреляционной связью называется такая статистическая связь, при которой различным значениям одной переменной соответствуют разные средние значения другой. Корреляционная связь может возникать несколькими путями. Важнейший из них – причинная зависимость вариации результативного признака от изменения факторного. Кроме того, такой вид связи может наблюдаться между двумя следствиями одной причины. Основной особенностью корреляционного анализа следует признать то, что он устанавливает лишь факт наличия связи и степень ее полноты, не вскрывая ее причин.
В экономическом анализе теснота измеряется линейным коэффициентом корреляции. Коэффициент корреляции при прямолинейной форме связи между факторами х и у определяется следующим образом:
При измерении тесноты связи при криволинейной форме зависимости используется не линейный коэффициент корреляции, а корреляционной отношение, которое рассчитывается по формуле:
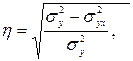
Данная формула является универсальной. Ее можно применять для исчисления коэффициента корреляции при любой форме зависимости. Однако для его нахождения требуется предварительное решение уравнения регрессии и расчет по нему теоретических (выравненных) значений результативного показателя для каждого наблюдения исследуемой выборки.
Значения коэффициента корреляции изменяются в интервале [–1; +1]. Значение г = –1 свидетельствует о наличии жестко детерминированной обратно пропорциональной связи между факторами, г = +1 соответствует жестко детерминированной связи с прямо пропорциональной зависимостью факторов. Если линейной связи между факторами не наблюдается, то r = 0. Другие значения коэффициента корреляции свидетельствуют о наличии стохастической связи, причем, чем ближе /r/ к единице, тем связь теснее.
При /r/ 0,7 – тесной.
Если коэффициент корреляции возвести в квадрат, получим коэффициент детерминации. Он показывает насколько процентов результативный показатель зависит от факторного.

Практическая реализация корреляционного анализа включает следующие этапы:
— постановка задачи и выбор признаков;
— сбор информации и ее первичная обработка (группировки, исключение, аномальных наблюдений, проверка нормальности одномерного распределения);
— предварительная характеристика взаимосвязей (аналитические группировки, графики);
— устранение мультиколлинеарности (взаимозависимости факторов) и уточнение набора показателей путем расчета парных коэффициентов корреляции;
— исследование факторной зависимости и проверка ее значимости;
— оценка результатов анализа и подготовка рекомендаций по их практическому использованию.
Регрессионный анализ состоит из нескольких этапов .
На первом этапе определяются факторы, которые оказывают воздействие на изучаемый показатель, и отбираются наиболее существенные для корреляционного анализа. Отбор факторов – очень важный момент в экономическом анализе: от того, насколько правильно он сделан, зависит точность выводов по итогам анализа. Не рекомендуется включать в корреляционную модель взаимосвязанные факторы. Если парный коэффициент корреляции между двумя факторами больше 0,85, то по правилам корреляционного анализа один из них необходимо исключить, иначе это приведет к искажению результатов анализа; нельзя включать в корреляционную модель факторы, связь которых с результативным показателем носит функциональный характер.
Большую помощь при отборе факторов для корреляционной модели оказывают аналитические группировки, способ сравнения параллельных и динамических рядов, линейные графики. С их помощью можно определить наличие, направление и форму зависимости между изучаемыми показателями. Отбор факторов можно производить также в процессе решения задачи корреляционного анализа на основе оценки их значимости по критерию Стьюдента.
На втором этапе собирается исходная информация по каждому факторному и результативному показателям. Она должна быть проверена на достоверность, на однородность и на соответствие закону нормального распределения.
В первую очередь необходимо убедиться в достоверности информации, насколько она соответствует объективной действительности. Использование недостоверной, неточной информации приведет к неточным результатам анализа и к неправильным выводам.
Одно из условий корреляционного анализа – однородность исследуемой информации относительно распределения ее около среднего уровня. Если в совокупности имеются группы объектов, которые значительно отличаются от среднего уровня, то это говорит о неоднородности исходной информации.
Критерием однородности информации служат среднеквадратическое отклонение и коэффициент вариации, которые рассчитываются по каждому факторному и результативному показателю.
Среднеквадратическое отклонение показывает абсолютное отклонение индивидуальных значений от среднеарифметической.
Оно определяется по формуле:
Коэффициент вариации показывает относительную меру отклонения отдельных значений от среднеарифметической.
Для его расчета используется формула:
Чем больше коэффициент вариации, тем относительно больший разброс и меньшая выравненность изучаемых объектов. Изменчивость вариационного ряда принято считать незначительной, если вариация не превышает 10%, средней – если вариация составляет 10-12%, значительной — когда она больше 20%, но не превышает 33%. Если же вариация выше 33%, то это свидетельствует о неоднородности информации и о необходимости исключения нетипичных наблюдений, которые обычно бывают в первых и последних ранжированных рядах выборки.
Следующее требование к исходной информации – подчинение ее закону нормального распределения. Для количественной оценки степени отклонения информации от нормального распределения служат отношение показателя асимметрии к ее ошибке и отношение показателя эксцесса к его ошибке.
Показатель асимметрии (А) и его ошибка (me) рассчитываются по следующим формулам:
Показатель эксцесса (Е) и его ошибка (me) рассчитываются следующим образом:
В симметричном распределении А = 0. Отклонение от нуля указывает на наличие асимметрии в распределении данных около средней величины. Отрицательная асимметрия свидетельствует о том, что преобладают данные с большими значениями, а с меньшими значениями встречаются значительно реже. Положительная асимметрия показывает, что чаще встречаются данные с небольшими значениями.
В нормальном распределении показатель эксцесса Е = 0. Если Е > 0, то данные густо сгруппированы около средней, образуя островершинность. Если Е Fтабл, то гипотеза об отсутствии связи между исследуемыми показателями отвергается.
Критерий Фишера рассчитывается следующим образом:
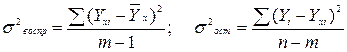
Yxi – индивидуальные значения результативного показателя, рассчитанные по уравнению;
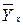
Yi – фактическое индивидуальное значение результативного показателя;
m – количество параметров в уравнении связи, учитывая свободный член уравнения;
n – количество наблюдений.
Для оценки точности уравнения связи рассчитывается средняя ошибка аппроксимации. Чем меньше теоретическая линия регрессии (рассчитанная по уравнению) отклоняется от фактической (эмпирической), тем меньше ее величина, а это свидетельствует о правильности подбора формы уравнения связи.
Средняя ошибка аппроксимации рассчитывается по формуле:
О полноте уравнения связи можно судить по коэффициентам множественной регрессии и детерминации. Если их значения близки к 1, значит в корреляционную модель удалось включить наиболее существенные факторы, на долю которых приходится основная вариация результативного показателя.
Влияние каждого фактора на прирост (отклонение от плана) результативного показателя рассчитывается по формуле:
Коэффициенты регрессии в уравнении связи имеют разные единицы измерения, что делает их несопоставимыми, если возникает вопрос о сравнительной силе воздействия факторов на результативный показатель. Чтобы привести их в сопоставимый вид, все переменные уравнения регрессии выражают в долях среднеквадратического отклонения, т.е. рассчитывают стандартизированные коэффициенты регрессии или бетта-коэффициенты (β)
Бета-коэффициенты показывают, что если величина фактора увеличится на одно среднеквадратическое отклонение, то соответствующая зависимая переменная увеличится или уменьшится на долю своего среднеквадратического отклонения. Сопоставление бетта-коэффициентов позволяет сделать вывод о сравнительной степени воздействия каждого фактора на величину результативного показателя.
Коэффициент эластичности рассчитывается по формуле:
Коэффициент эластичности показывает, на сколько процентов в среднем изменится функция с изменением аргумента на 1%.
Перечисленное многообразие методов предоставляет аналитику широкие возможности в выборе инструментария исследования, как в экономическом анализе, так и в рамках финансового анализа. Выбор того или иного способа или приема из перечисленных определяется целью экономического (финансового) анализа, требованиями к степени детализации (глубины) анализа, к точности результатов (например, «разложение» результативного показателя по факторам), характером взаимосвязи между показателями, характером аналитических задач.
Независимо от выбранных способов алгоритм решения практически любой аналитической задачи содержит приемы сравнения, группировки, балансовой увязки и графический, которые рассматриваются как способы обработки первичной, исходной информации.
Источник