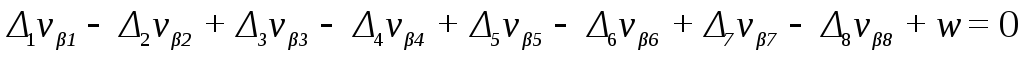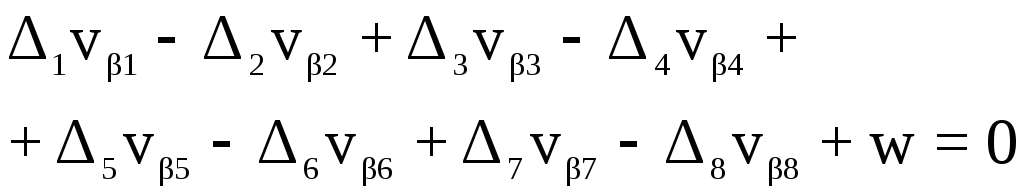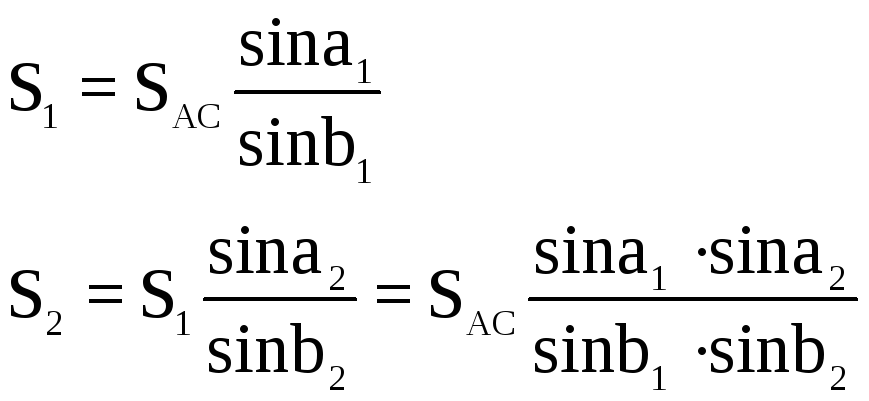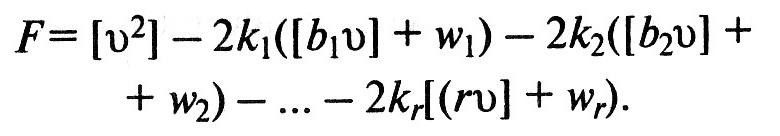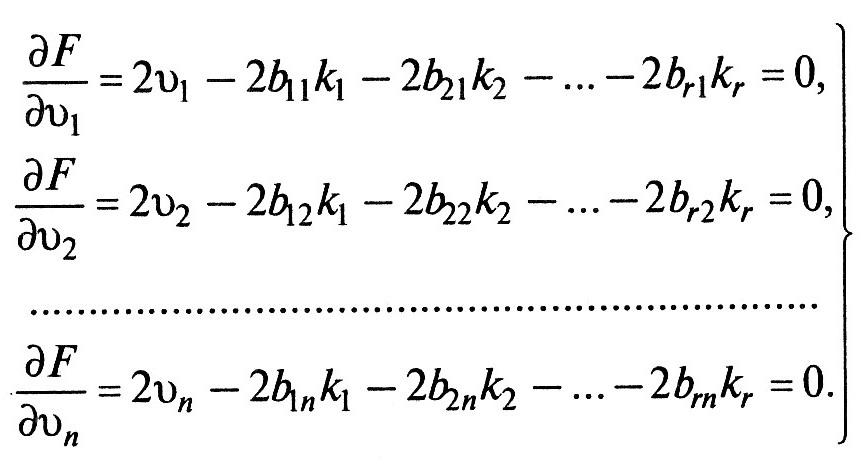- 7.3 Коррелатный способ уравнивания
- 8 Коррелатный способ уравнивания триангуляции
- 8.1 Виды условных уравнений в триангуляции при коррелатном способе уравнивания
- Коррелатный способ уравнивания что это
- 54.Сущность коррелатного способа уравнивания.
- 53.Вычислительная обработка сетей сгущения. Общие сведения об уравнивании геодезических сетей.
- 52.Способы определения дополнительных пунктов. Способы: засечек, передачи координат с вершины знака на землю.
7.3 Коррелатный способ уравнивания
Коррелатный способ основан на использовании функциональной связи между собой элементов геодезических построений Xi (i = 1, n). Эти уравнения связи называются условными уравнениями:
При коррелатном способе уравнивания вначале составляется система условных уравнений AV + W = 0,
где А – матрица коэффициентов системы условных уравнений;
V – вектор поправок в измеренные значения элементов сети;
W – вектор невязок условных уравнений.
При этом коэффициенты aij условных уравнений поправок определяются по формуле:
а невязки уравнений – по формуле:
где xi (i = 1, n) – измеренные значения элементов геодезических построений.
При известной весовой матрице Р вначале вычисляют обратную весовую матрицу Q = P -1 , а затем от системы условных уравнений переходят к системе нормальных уравнений:
Определив коррелаты К = — (AQA T ) W, вычисляют поправки V = QA T K и уравненные значения измеренных элементов сети x* = x + v,
где х* – вектор уравненных значений;
х – вектор измеренных значений элементов геодезических построений.
8 Коррелатный способ уравнивания триангуляции
8.1 Виды условных уравнений в триангуляции при коррелатном способе уравнивания
Рассмотрим условные уравнения, возникающие при уравнивании углов триангуляции. При этом углы редуцированы на плоскость проекции Гаусса-Крюгера и исправлены за центрировку прибора и редукцию визирных целей.
8.1.1 Условие фигур. Сумма измеренных углов в замкнутой фигуре (например, в треугольнике) должна быть равна теоретической.
Рисунок 8.1 – Условие фигур
8.1.2 Условие суммы углов (условие станции). Условие возникает при измерении на станции углов между смежными направлениями и углов, являющихся суммой измеренных углов.
Рисунок 8.2 – Условие суммы углов
8.1.3 Условие горизонта. Возникает в случаях, когда на станции измерены углы с замыканием горизонта.
Рисунок 8.2 – Условие горизонта
8.1.4 Условие полюса (боковое условие). Полюсное условие заключается в требовании, чтобы длина стороны, вычисленная двумя независимыми путями из решения треугольников сети, имела одно и тоже значение.
Рисунок 8.4 – Условие полюса
Рисунок 8.5 – Частный случай условия полюса
8.1.5 Условие исходных дирекционных углов (азимутальное условие). Условие возникает в сети, в которой две или более сторон сети имеют значения дирекционных углов, не подлежащие изменению при уравнивании.
Рисунок 8.6 – Условие исходных дирекционных углов
При этом выбор ходовой линии не имеет значения. Частный случай:
Рисунок 8.7 – Частный случай условия исходных дирекционных углов
8.1.6 Условие базисов возникает в случаях, когда в сети имеется две или более сторон, длины которых не подлежат изменению в процессе уравнивания. Условие базиса заключается в требовании, чтобы длина одной исходной стороны, полученная от другой исходной стороны решением треугольников совпадала с заданным ее значением.
Рисунок 8.8 – Условие базисов
Рисунок 8.9 – Частный случай условия базисов
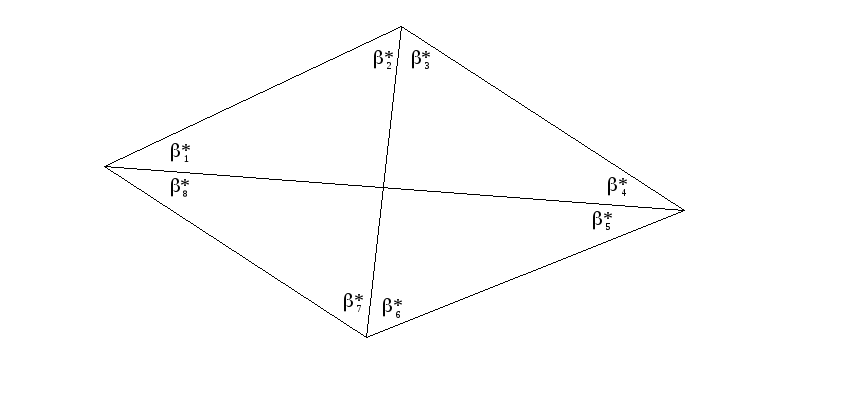
8.1.7 Условие координат возникает в том случае, если в сети имеется два и более разобщенных между собой исходных пункта с координатами, не подлежащими изменению при уравнивании. Для составления уравнений координат из сети выделяют простую и наиболее короткую цепь треугольников, соединяющих два исходных пункта.
Рисунок 8.10 – Условие координат
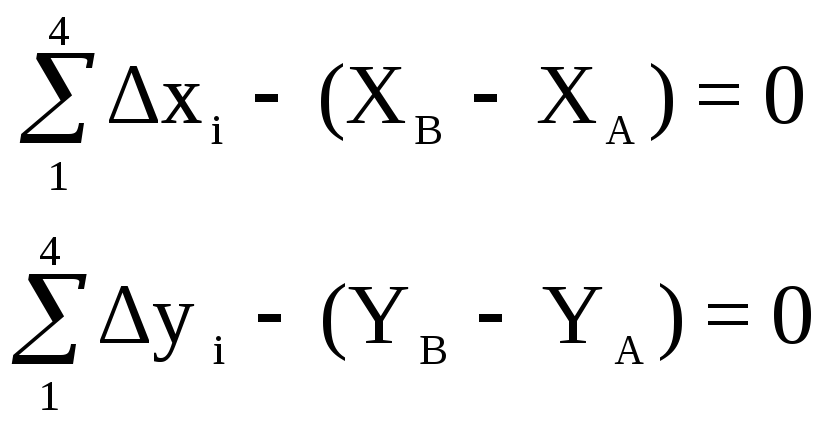
где 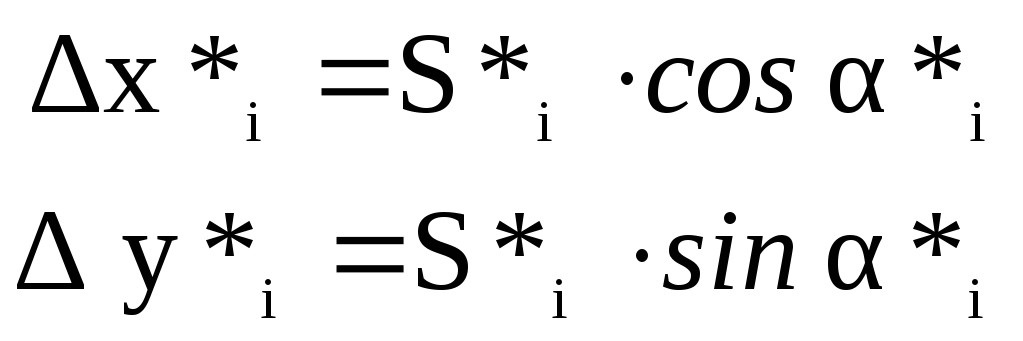

С учетом малости поправок 
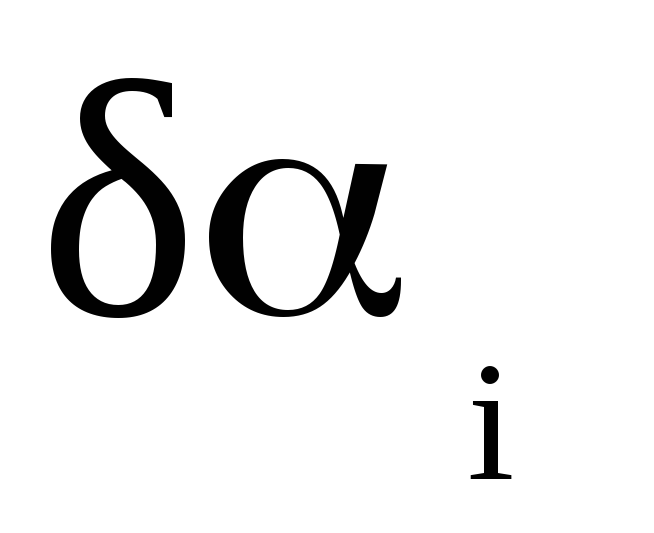


где 
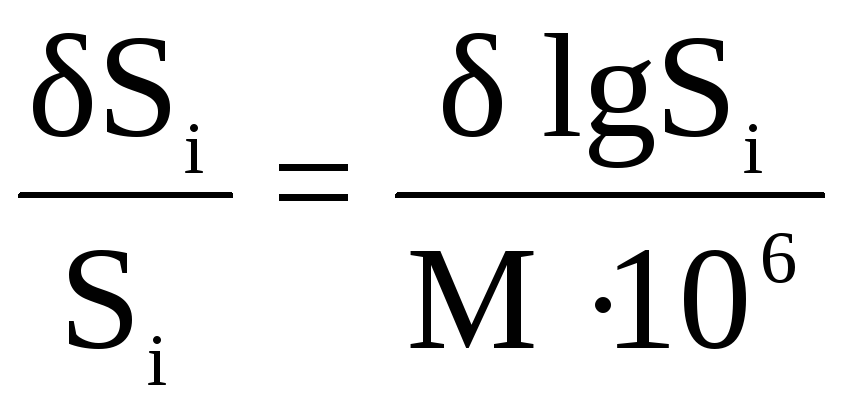
где lg Si – изменение lg Si, соответствующее поправке 
М = 0,43429 – lg e – модуль натуральных логарифмов.

Подставим эти уравнения в исходные условные уравнения и получим:

где 
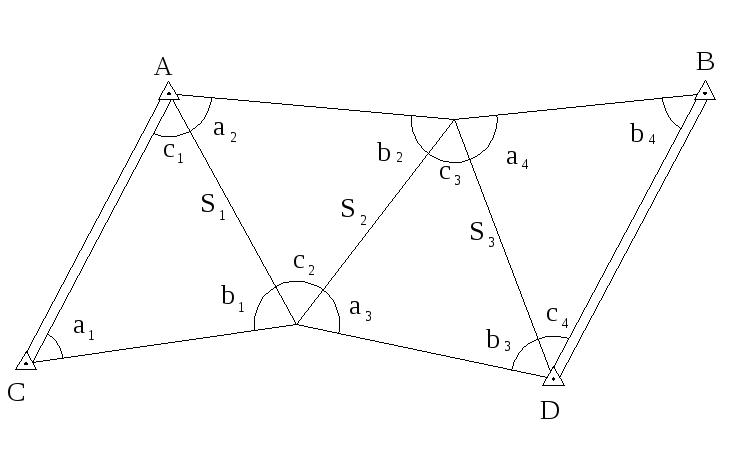
Выразим длины и дирекционные углы ходовой линии через измеренные углы треугольников сети триангуляции:
Из этого следует, что i и Si независимы, так как i вычисляются через промежуточные углы ci, а стороны Si вычисляются при помощи связующих углов ai и bi. Независимость поправок i и Si существенно упрощает составление условных уравнений координат. Определим поправки:
lg S2 = 
lg S3 = 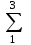
lg S4 = 
Подставляя i и lg Si в условные уравнения получим в окончательном виде:
Источник
Коррелатный способ уравнивания что это
Метод наименьших квадратов
Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатам измерений, содержащим случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке геодезических измерени.
Метод наименьших квадратов содержит в себе 2 основных способа: коррелатный и параметрический, которые при строгом уравнивании дают одинаковые результаты. Выбор способа обычно зависит от объема вычислений, определяемого в основном количеством совместно решаемых уравнений, т.е. конфигурацией сети. Коррелатный способ более оптимален для свободных сетей и сетей с небольшим числом исходных пунктов и большим числом определяемых — по-скольку количество уравнений равно числу избыточных измерений. Параметрический способ, наоборот, выгоден для сетей с большим числом исходных и малым числом определяемых, по-скольку количество уравнений будет равно числу необходимых измерений.
Идея коррелатного способа заключается в отыскании поправок к измеренным величинам через вспомогательные неопределенные множители, называемые коррелатами. Сущность уравнивания коррелатным способом состоит в том, что задачу нахождения минимума функции уравнения разложенного по ряду Тейлора решают по способу Лагранжа с определенными коррелатами, в результате чего получают коррелатные уравнения поправок (векторы поправок). Преобразовав уравнения поправок получают нормальные уравнения коррелат, через которые находят вероятнейшие значения поправок.
Параметрический способ подразумевает вычисление поправок не к измеренным величинам, а к каким-то приближенным значениям (параметрам), т.е. к конечным результатам уравнения, которыми в геодезических сетях являются координаты или высоты пунктов, и непосредственное получение вероятнейших значений параметров, минуя вероятнейшее значение измеренных элементов сети.
Метод наименьших квадратов был предложен К. Ф. Гауссом (1794-95) и А. Лежандром (1805-06). Первоначально этот метод использовался для обработки результатов астрономических и геодезических наблюдений. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов даны А. А. Марковым и А. Н. Колмогоровым. Ныне способ представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.
Источник
54.Сущность коррелатного способа уравнивания.
Коррелатный способ уравнивания. Он состоит в следующем. Пусть уравниваемой геодезической сети соответствует система независимых условных уравнений поправок
Рассмотрим решение задачи по определению поправок для случая равноточных измерений в соответствии с принципом [гг] = тт. Эта задача относится к математическому анализу на условный экстремум. Она может быть решена с помощью множителей Лагранжа, называемых коррелатами.
Для такого решения составляют функцию Лагранжа
Затем функцию исследуют на экстремум, для чего находят ее частные производные и приравнивают их к нулю:
Равенства называют коррелатными уравнениями поправок.
Подставляя выражения поправок (14.11) в условные уравнения (14.8), после приведения подобных членов получаем систему уравнений
которую называют системой нормальных уравнений коррелат.
53.Вычислительная обработка сетей сгущения. Общие сведения об уравнивании геодезических сетей.
В геод сетях для контроля и оценки качества измерений, повышения их точности наряду с необходимыми выполняют и избыточные измерения. Необход и избыт измерения нах-ся в опр-х матем отношениях, в процессе решения которых они должны быть разрешены. В виду присутствия ошибок в рез-ах геометр условия не соблюдаются точно, что приводит к появлению невязок, которые должны быть устранены путем введения поправок, избыочные измерения позволяют получать искомые величины несколькими путями. Т.к. ошибки в измерениях неизвестны и явл случайными, то логично поставить при уравнивании такое условие, чтобы найденные поправки в измерении как можно меньше бы искажали результат. Такой принцип был предложен франц математиком Ле Жандром, затем Гауссом, а теперь наз способ наим квадратов.
При этом соблюд след условия:
-выполнение всех геометрических условий, возникших в сети
-нахождение наиболее надежных значений измеренных величин под условием суммы квадратов минимума поправок.
-оценку точности квадратов поправок и их ф-ий проводят по полученным результатам.
52.Способы определения дополнительных пунктов. Способы: засечек, передачи координат с вершины знака на землю.
Дополнительные (уединенные) пункты устанавливают для сгущения геодезической сети до необходимой плотности пунктами съемочного обоснования. Плановое положение этих пунктов определяют: передачей координат с вершины знака на землю, прямой, обратной, комбинированной и линейной засечками, лучевыми и полярными системами.
Координаты с вершины знака на землю передают в том случае, когда необходимо привязать полигонометрический (теодолитный) ход к пункту существующей сети, на котором нельзя встать с прибором (шпиль башни, колокольня церкви и др.). Для привязки хода выбирают вблизи пункта на земле пункт Р с таким расчетом, чтобы с него был виден пункт А и два удаленных исходных пункта В и С (один из них для контроля определения координат пункта Р и было удобно измерить два базиса для определения недоступного расстояния АР.
Сущность прямой засечки состоит в определении координат третьего пункта по координатам двух исходных пунктов, двум исходным дирекционным углам (в случае отсутствия видимости между исходными пунктами) и двум измеренным углам при исходных пунктах.
Для контроля правильности определения координат измеряют еще угол при третьем исходном пункте. Таким образом, для решения задачи с контролем необходимо видеть определяемый пункт с трех исходных и измерить при них три угла. Углы между смежными направлениями на определяемый пункт должны быть не менее 30 и не более 150°. Существуют различные формулы и схемы для решения задачи прямой засечкой.
ф-лы Юнга
ф-лы Гаусса
Сущность обратной засечки заключается в определении координат четвертого пункта по координатам трех исходных пунктов и двум углам, измеренным при определяемом пункте.
Для контроля правильности решения задачи при определяемом пункте измеряют третий угол между направлениями на один из первых трех пунктов и на четвертый пункт исходной сети.
Таким образом, для решения задачи с контролем необходимо видеть из определяемого пункта четыре пункта исходной сети и измерить три угла при определяемом пункте.
Существует много способов решения задачи: ф-ла Кнейссля.
Сущность линейной засечки состоит в определении координат пункта по координатам двух исходных пунктов и по двум расстояниям от определяемого пункта до исходных.
Источник