Координатный способ определения положения частицы

Так как координата точки указывает расстояние до начала отсчета, то ее размерность — размерность длины.

Рассмотрим теперь эти известные математические положения с физической точки зрения. Пространство, в котором мы живем, не имеет «выделенных» точек и направлений, с которыми раз и навсегда можно связать единую и абсолютную систему отсчета. Поэтому положение данного тела можно определить только относительно других тел. В связи с этим начало отсчета физической системы координат удобно связывать с некоторым конкретным телом (которое называется тело отсчета). Направления осей координат также следует связывать с другими материальными телами. В качестве единицы длины используются эталоны, которые воспроизводятся с помощью физических приборов. В международной системе единиц СИ единицей длины является метр. Подчеркнем, что выбор всех элементов системы координат, в принципе, является

произвольным, следовательно, координаты точки относительны. Иными словами, числа-координаты имеют смысл только в том случае, если задана система координат, то есть положение данного тела определяется относительно других тел, с которыми связана система координат. Во многих случаях задание трех координат точки является излишним. Так если тело движется вдоль заданной (известной) прямой, то имеет смысл одну из осей (скажем X ) направить вдоль этой прямой. Тогда оставшиеся координаты ( x, y) все время будут равны нулю, поэтому их можно не принимать во внимание. Заметим, что аналогичным образом можно ввести координаты точки на произвольной заданной линии, измеряя длину участка этой линии между данной точкой и началом отсчета и указывая с помощью знаков с какой стороны от начала отсчета находится точка. Аналогично, при движении тела по заданной плоскости (и даже произвольной поверхности), достаточно определить в этой плоскости две оси координат.

Эквивалентным координатному является векторный способ описания положения. В рамках этого метода положение точки в пространстве задается с помощью радиус-векора r͞͞,вектора, соединяющего начало координат с рассматриваемой точкой. Координатами этого вектора являются декартовые координаты точки (x,y,z).

Источник

Координатный способ определения положения частицы

Движение. Виды движений. Описание движения. Система отсчета.

Механическим движением тела (точки) называется изменение его положения в пространстве относительно других тел с течением времени.

А) Равномерное прямолинейное движение материальной точки.

Б) Равноускоренное прямолинейное движение материальной точки.

В) Движение тела по дуге окружности с постоянной по модулю скоростью.

Г) Гармоническое колебательное движение. Важным случаем механического движения являются колебания, при которых параметры движения точки (координаты, скорость, ускорение) повторяются через определенные промежутки времени.

1. Векторный способ описания движения

ОПРЕДЕЛЕНИЕ: Векторный способ описания движения – это описание изменения радиус-вектора материальной точки в пространстве с течением времени.

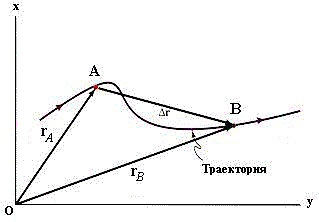
Рассмотрим движение точки М в некоторой системе отсчета Oxyz (рис.1). Зададим радиус-вектор точки r — вектор, соединяющий начало координат с этой точкой.

При движении точки M вектор r будет с течением времени изменяться, т.е. будет каким-то образом зависеть от времени. Эта зависимость r = r ( t ) представляет собой закон движения в векторном виде.

В процессе движения конец радиус-вектора будет описывать траекторию, а его изменение – перемещение s точки.

2. Координатный способ описания движения

ОПРЕДЕЛЕНИЕ: Координатный способ описания движения – описание изменения во времени координат точки в выбранной системе отсчета.

В декартовой системе координат положение точки определяется тройкой чисел ( x , y , z ) — ее декартовыми координатами.

Чтобы задать закон движения точки, необходимо знать значения ее координат в каждый момент времени. Закон движения в координатном виде в общем случае представляет собой систему трех уравнений: x = x ( t ), y = y ( t ), z = z ( t )

Между векторным и координатным способом описания движения существует непосредственная связь, а именно: числовые значения проекций радиус-вектора движущейся точки на координатные оси системы с тем же началом отсчета равны координатам точки: r_x = x , r_y = y , r_z = z .

3. Естественный способ описания движения

ОПРЕДЕЛЕНИЕ: Естественный способ описания движения – описание движения вдоль траектории. Этим способом пользуются, когда траектория точки заранее известна.

Пусть точка М движется вдоль траектории АВ в системе отсчета Oxyz (рис.3). Выберем на траектории какую-нибудь неподвижную точку О 1 , которую будем считать началом отсчета, и определим положительное и отрицательное направления. Тогда положение точки M будет определяться расстоянием S от точки О 1 . При движении точка М переместится в точку М 1 , соответственно изменится ее расстояние от точки О 1 . Таким образом, расстояние S зависит от времени, а характер этой зависимости позволит определить положение точки М на траектории в любой момент времени. Закон движения в этом случае имеет вид: s = s ( t ) .

Под системой отсчета понимают тело отсчета, которое условно считается неподвижным, систему координат, связанную с телом отсчета, и часы, также связанные с телом отсчета. В кинематике система отсчета выбирается в соответствии с конкретными условиями задачи описания движения тела.

Источник

Координатное и векторное описание положения частицы. Связь между ними

Пусть траектория движения известна. Тогда, зная зависимость пути, пройденного телом, от времени, можно определить его положение в любой момент. Положение тела в пространстве можно задать также в виде радиуса-вектора r. В произвольный момент времени оно определяется зависимостью r(t). Вектор перемещения s(t) рассчитывается как разность между величинами радиуса-вектора r(t) в различные моменты времени t.

На рисунке тело в момент времени t₁ находилось в точке A, а в момент t₂ — в точке B.

Координатный способ описания движения. Поскольку векторная величина может быть представлена как сумма ее проекций, то положение тела в пространстве в любой момент времени можно определить, исходя из зависимостей от времени проекций радиуса-вектора на оси координат x(t), y(t), z(t).

Пример. В качестве одного из примеров координатного способа можно привести описание движения тела, брошенного под углом a к горизонту. Движение по горизонтали происходит с постоянной скоростью, следовательно, x = V₀·sin(a)·t. Движение по горизонтали является равнопеременным с ускорением свободного падения g, следовательно, y = V₀·cos(a)·t — g·t₂/2. Исключив из этих уравнений время, получим, что траектория — зависимость y = f(x) представляет из себя параболу.

Скорость и ускорение материальной точки.

Материальная точка при своем движении описывает некоторую линию. Эта линия называется траекторией. В зависимости от формы траектории различают прямолинейное движение, движение по окружности, криволинейное движение и т.д. под скоростью понимают путь, проходимый частицей за единицу времени. Если за равные, сколь угодно малые промежутки времени частица проходит одинаковые пути, движение частицы называют равномерным. В этом случае скорость, которой обладает частица в каждый момент времени, можно вычислить, разделив путь s на время t.в физике под скоростью понимают векторную величину, характеризующую не только быстроту перемещения частицы по траектории, но и направление, в котором движется эта частица в каждый момент времени. Разобьем траекторию на бесконечно малые перемещение dr. Разделив это перемещение на соответствующий промежуток времени dt, получим мгновенную скорость в данной точке траектории. Получим: v=dr/dt=r.Т.о. скорость есть производная радиуса-вектора частицы по времени. Элементарное перемещение частицы равно dr=v*dt.

Скорость частицы v может изменяться со временем как по модулю,так и по направлению. Быстрота изменения вектора , как и быстрота изменения любой функции времени, определяется производной вектора v по t. Обозначив эту производную буквой w, получим w=dv/dt=v. Величина определяемая данной формулой называется ускорением частицы.

Равнопеременное движение.

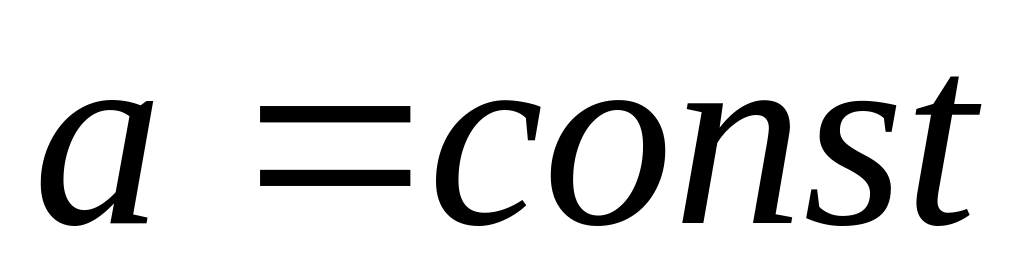
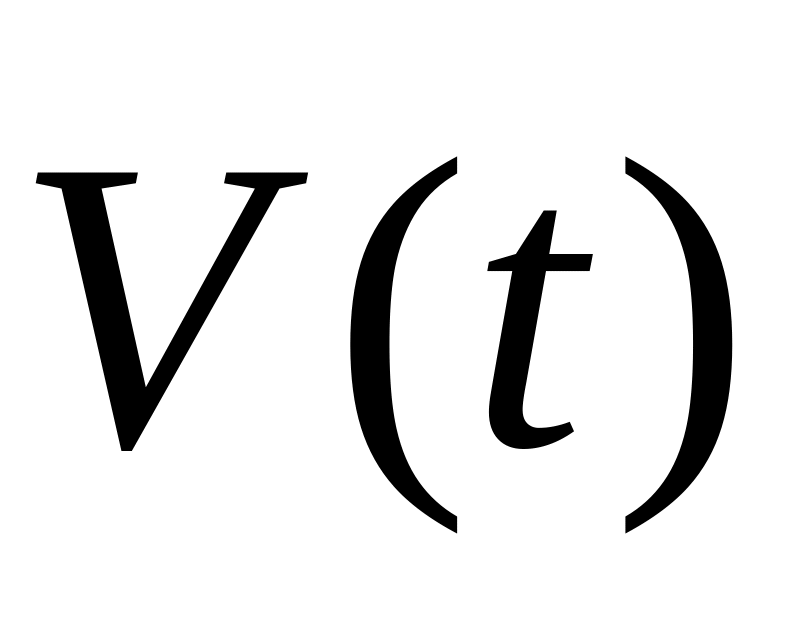
Движение материальной точки называется равнопеременным, если ускорение остается постоянным по величине и направлению с течением времени: . Вычислим и . Для этого запишем: ,

.

Итак, 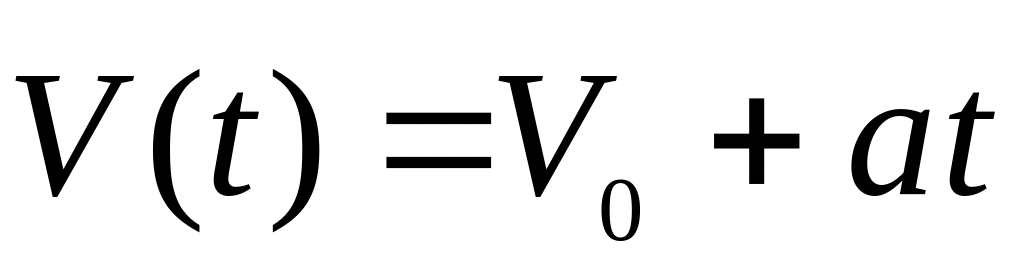, . Спроецируем равенства на оси декартовой системы координат. Получим,

,

.

Здесь, — проекции скорости частицы в нулевой момент времени, — проекции ускорения частицы, — координаты частицы в нулевой момент времени, — координаты частицы в момент времени .

Источник