Конструктивный способ решения задач

Решение конструктивных задач

Задачи начертательной геометрии можно условно разделить на позиционные, метрические и конструктивные задачи. Наибольший интерес представляют конструктивные задачи, решение которых опирается на теорию решения позиционных и метрических задач. Под конструктивными задачами понимаются задачи, связанные с построением геометрических образов, отвечающих определенным условиям.

Роль и значение конструктивных задач:

1. Вызов любознательности

2. Учат логически мыслить

3. Развивают пространственное мышление

4. Учат проводить анализ и исследование

5. Дают возможность геометрически истолковывать уравнения, неравенства.

Решение конструктивных задач основывается на теории начертательной геометрии, алгебре множеств и геометрических местах элементов, поэтому приступать к решению этих задач можно только после того, как начитан материал «методы преобразования эпюра», а также повторен материал элементарной геометрии и ознакомления с множествами.

Множество есть понятие первоначальное, неопределяемое, обще математическое. Множество есть многое, мыслимое нами как единое (Георг Кантор). Предметы, составляющие данное множество, называются его элементами. Множества могут состоять не только из чисел, но и других понятий (табун, лес, геометрическая фигура, группа и т.п.). Множество называется конечным, если оно содержит конечное число элементов (число деревьев в лесу, число студентов в группе). Множество может состоять даже из одного элемента. Пустое множество не содержит ни одного элемента (нулевой отрезок). Множество называется бесконечным, если в нем бесконечно много элементов (множество точек на окружности).

Так, например, определение на прямой линии l точки, удаленной от точки С на расстояние 30 мм. Конструктивные задачи целесообразно решать в такой последовательности: анализ задачи, её исследование, составление пространственного плана (алгоритма) решения и доказательство правильности решения. Целью анализа является разбиение задачи путем рассуждений на составные части (множества) и установление связи между заданными и искомыми величинами. Множество точек, удаленных от точки С на расстояние 30 мм, представляет собою сферу с центром в точке С и радиусом 30 мм. Ответом являются точки пересечения прямой линии l со сферой. Целью исследования является установление возможного количества решений и тех параметров, от которых зависит это количество ответов. В нашем примере количество решений зависит от взаимного расположения геометрических образов. Если расстояние между точкой и прямой больше радиуса сферы, то задача не имеет решения. Если расстояние между точкой и прямой меньше радиуса сферы, то задача имеет два решения. Если расстояние между точкой и прямой равно радиусу сферы, то задача имеет одно решение (касание прямой линии со сферой). Очень часто анализ дает сжатый алгоритм, который затем разворачивается в план графического решения задачи (см. 4.3.2 , рис. 4.8). Целью доказательства является установление правильности решения на основе всех правил и теорем начертательной геометрии.

Рассмотрим ещё пример. Даны три скрещивающиеся прямые линии а, b и с, требуется провести четвертую прямую линию d, параллельно прямой с и пересекающую прямые а и b (рис. 5.24). Множество прямых, параллельных прямой c и пересекающих а, определяет плоскость α. Множество прямых, параллельных прямой с и пересекающих b, определяет плоскость β. Плоскости α и β пересекаются по прямой d. Задача всегда имеет одно решение, так как плоскости в пространстве всегда имеют пересечение по собственной или несобственной прямой линии.

Рис. 5.24. Проведение прямой линии d параллельно прямой линии с и пересекающей прямые линии а и b

z

На рис. 5. 25 приведен пример решения неравенства: x ≥ 3; y ≥ 4; z ≥ 0; x + 0, 5 y + z ≤ 8.

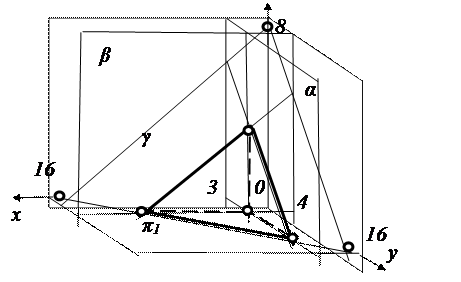Рис. 5.25. Решение неравенств

Первому неравенству отвечает множество точек, расположенных левее плоскости α, второму неравенству отвечает множество точек, расположенных впереди плоскости β, третьему неравенству отвечает множество точек, расположенных выше плоскости π, и наконец, четвертому неравенству отвечает множество точек, расположенных за плоскостью γ. В пересечении плоскостей α, β, π₁ и γ получается прямоугольная пирамида, которая отвечает решению заданной системы неравенств.

На практике не существует, задач в чистом виде сформулированных на языке геометрии. Все задачи носят реальной физический характер. На первом этапе геометрического моделирования реально существующая проблема описывается геометрическими терминами, т.е создается геометрическая модель исходного явления, которая позволяет с помощью некоторого алгоритма сопоставить исходным параметрам ответный результат. В дальнейшем полученная модель анализируется и исследуется, в результате чего идее усовершенствование модели. Когда сконструированная модель становится достаточно удобной или, по крайней мере, уже не видно путей её дальнейшего усовершенствования, возникает необходимость в её реализации и создании какого-либо технического устройства.

Развитие начертательной геометрии идет в следующих направлениях:

· систематизация, дальнейшее развитие и широкое применение существующих геометрических алгоритмов;

· анализ и систематизация численно-знаковой информации и дальнейшая разработка правил и законов чтения и выполнения чертежей различных отраслей производства для создания программного обеспечения машинной графики;

· изучение законов зрительного восприятия и особенностей наглядных изображений;

· изучение различных свойств геометрических моделей и методов геометрического моделирования применительно к конкретным специальностям;

· интеграция и обновление содержания образования через универсальные геометрические модели.

Источник

Нестандартные решения сложных задач

Меня интересуют различные методы системного и творческого мышления, которое можно использовать в реальной жизни для решения сложных задач. О нескольких методах расскажу в данной статье.
Недавно прочитал книгу Торп С. — Учебник креативного мышления. Простой подход к нестандартным решениям – 2010. В ней предлагается интересный подход для развития навыков решения сложных задач.

Основная мысль автора – чтобы решать сложные задачи, нужно сворачивать с колеи шаблонного мышления, нарушать правила, которые зачастую нам не дают взглянуть на проблему шире. Вот что пишет автор:

Неспособность разрешить какую-то проблему вполне может объясняться тем, что вы застряли в «колее» правил. Мы все живем по правилам — укоренившимся в нас шаблонам мышления, которые ошибочно принимаем за истину. Наши правила формируются естественным образом в результате многократного использования одних и тех же идей. Следуя правилам, мы постепенно увязаем в глубокой «колее», и тогда любые неординарные идеи остаются вне нашего поля зрения.

Как нарушать правила, отлично показано на примере игры «Крестики-нолики».
Многие неразрешимые проблем похожи на игру в «крестики-нолики»» Выигрыш кажется невозможным, как бы ты не играл. Однако нарушив (или расширив) правила можно получить победу множеством путей.

Ход вне очереди

В «крестики-нолики» выиграть очень просто, если делать ходы вне очереди! Конечно в контексте крестиков-ноликов, нарушение правил – это обман. Однако речь идет не о моральных принципах, а о правилах, которые предписывают нам, как следует решать проблему.

Если правила не работают, то почему бы не сыграть на опережение, делая дополнительные ходы.
Мало кому приходит в голову сделать ход вне очереди в реальном мире, но, в сущности, этот прием используется с незапамятных времен. Например, после одного из сражений гражданской войны в Америке генерал Роберт Ли объявил своим офицерам, что генерал Грант двинется на Спотсильванию, так как это наилучшее для него решение. Ли разработал кратчайший маршрут к этому пункту и приказал войскам двигаться туда. Войска Ли сделали, так сказать, ход вне очереди и прибыли в Спотсильванию прежде, чем туда смогла добраться армия Гранта.

Ходы вне очереди — распространенное явление в мире бизнеса. Когда изготовители Тайленола узнали, что аналогичное обезболивающее средство Датрил будет продаваться со значительной скидкой, они сделали ход вне очереди. Они установили цену ниже стоимости Датрила еще до того, как изготовители последнего смогли объявить о своей цене. Рекламная кампания нового лекарства провалилась, и Тайленол удержал свои позиции на рынке.

Мы в компании, часто играем на опережение – ещё на предварительном изучении объекта автоматизации разрабатываем прототип системы. Такой подход нам позволяет глубже понять, что нужно сделать, а заказчику увидеть серьёзность наших намерений.

Используйте активы соперника

Выстроить в ряд три значка совсем не трудно, если к своим двум ноликам прибавить чужой крестик. Зачем ограничивать себя собственными ресурсами? )

Адмирал военно-морского флота США Гарри Ярнелл был первым, кто разработал план нападения японцев на Перл-Харбор. Он определил наиболее перспективные направления и стратегию атаки. В 1932 году он даже провел показательные учения с участием двух авианосцев США. Императорский военно-морской флот Японии превратил план американского адмирала в собственную успешную атаку на базу ВМС США. Японцы не постеснялись воспользоваться американским планом сражения. Если план эффективен, осознано используйте его, независимо от источника.

В шашках и шахматах победная комбинация основывается на расположении, как своих фигур, так и противника, причем именно использование фигур противник зачастую является ключевым элементом победного плана.
В бизнесе предприниматели часто изучают что сдали конкуренты, учитывают их ошибки и создают более прибыльную систему.

Проявите гибкость (и правильно ставьте задачи)

Вы сможете выиграть в «крестики-нолики» или разрешить другие сложные задачи, если примените гибкое определение термина «победа». Позвольте вашему ряду изогнуться, и победа у вас в кармане. Иногда определенные нами условия победы слишком строги или не соответствуют характеру сложившейся ситуации. Измените определение успеха и решение станет возможным.
Кроме того, если задача была поставлена неправильно, то возможно никому не под силу её решить. Задача должна ставиться конструктивно, в расчете на нетривиальные решения, отличные от ваших первоначальных ожиданий. Деструктивная постановка задач связана с таким количеством условий и ограничений, что достижение цели оказывается за пределами человеческих возможностей. Примером деструктивной постановки задачи может быть желание «летать, махая руками, словно крыльями».
При конструктивной постановке задачи приемлемым будет любое решение, позволяющее вам «оторваться от земли». Правильная постановка задачи расширяет диапазон возможных решений.

Сотрудничайте

Правило, ведущее к обязательному проигрышу одной стороны, может оказаться самым большим препятствием на пути к победе любого из участников игры. Сотрудничество с соперником может обеспечить выигрыш вам обоим.
Однажды я услышал фразу на всегда запавшую мне в душу: «В одного можно вырастить только супер-картошку!!». Имеется ввиду, что для решения действительно сложных задач нужна команда и желание сотрудничать.

Пробуйте решать сложные проблемы – нарушайте правила!

Источник

Как построить пример? Решение задач на конструктивы

Это учебная статья по математике, перед началом занятий мы рекомендуем ознакомиться с вводной частью

В математике часто встречаются задачи, в которых вопрос звучит следующим образом: «Можно ли …?» «Существует ли …?» Возможно, что задачи, которые вы решали, звучали так: «Нарисуйте…», «Постройте…», «Найдите среди…» Но везде, в каждой такой задаче, требовалось придумать какой-нибудь пример или что-то выбрать из предложенных предметов. Например, в теме «Разрезания» была такая задача:

Задача 1.

Разрежьте квадрат 4 ✕ 4 на 4 равных фигурки, каждая из которых состоит из 4 клеточек, составленных в форме буквы Т.

Решение.

Мы строили требуемое постепенно. Поставили одну такую фигурку в угол квадрата, а затем по аналогии заполнили всю оставшуюся часть квадрата такими же фигурками.

Ответ:

Задача 2.

Нарисуйте 9 квадратиков, как на картинке сверху, выберите карандаши трёх разных цветов и раскрасьте квадраты так, чтобы в каждой строчке и в каждом столбике были квадраты всех трёх цветов.

Алгоритм решения этой задачи может быть различным. Самый простой – раскрасим в три цвета первый ряд. Например, так, как сверху: красный, жёлтый, синий. Посмотрим на второй ряд и раскрасим первый квадрат в любой, отличный от красного цвет. Пусть синий. Тогда второй квадрат в этом ряду можно раскрасить уже только в красный цвет, а оставшийся – только в жёлтый. Для третьего ряда уже есть только один вариант.

Ответ:

Напомним ещё одну задачу.

Задача 3.

Расставьте вдоль стен большой квадратной комнаты а) 4 стула; б) 5 стульев; в) 7 стульев так, чтобы у каждой стены стояли по два стула. (В центр комнаты стулья ставить нельзя.)

Решение.

В каждом пункте, если ставить по два стула у стены, стульев не хватит. Поэтому нужна идея, как обойтись меньшим числом стульев. То есть решить, куда нужно поставить стул, чтоб он оказался одновременно у двух стен?

Пункт а). Если поставить стул в угол, то он будет стоять сразу около двух стен; а так как углов всего 4, и каждая стена оканчивается двумя углами – то, использовав всего 4 стула, мы сможем поставить около каждой стены по 2 стула (см. рис.).

Пункт б). Для того чтобы поставить 5 стульев, не нарушив условия, нужно передвинуть 1 стул из угла к середине стены. Тогда около соседней стены останется только 1 стул. Туда и поставим пятый стул, но не в угол, а посередине. Таким образом, в комнате стоит 5 стульев, и условие задачи выполнено.

Пункт в). Аналогичным образом (передвинув 1 стул из угла к середине стены и поставив шестой стул в центре соседней стены) мы сможем добиться сначала расстановки 6 стульев, а затем и 7.

Конечно, можно было решать эту задачу по-другому: расставить сначала 8 стульев – по два у каждой стены, а потом, убирая по одному стулу, решать, как распределить остальные стулья.

Что общего между всеми этими задачами? И в том и в другом случае мы строили пример или конструкцию. Такие задачи называются «задачами на конструкцию» или «конструктивными».

Рассмотрим ещё несколько задач.

Задача 4.

Директор вызвал трёх учеников и поставил их в ряд. У одного из них испорченный дневник. За один ход ученик передаёт дневник незаметно для директора соседу. Директор за свой ход может проверить одного ученика. Ходят по очереди, начинает директор. Как должен действовать директор, чтобы обнаружить дневник?

Решение.

Директор должен проверить ученика, стоящего по центру. Если у него нет дневника, то на следующий ход дневник будет у него, так как у остальных двоих нет других соседей. Директор проверит своим вторым ходом снова стоящего по центру ученика и обнаружит дневник.

Задача 5.

Расставьте в таблице 3 × 3 числа от 1 до 9 так, чтобы сумма трёх чисел в любой строке и любом столбце была одной и той же.

Решение.

Чтобы подсчитать, какая сумма должна быть в каждой строке, надо посчитать сумму чисел от 1 до 9 (= 45). Всего строк три. Значит, 45 надо разделить на 3. Даже если ребёнок не проходил деления, тем не менее, мы надеемся, что он сможет сообразить, как разделить 45 предметов на три равные по количеству предметов группы. Значит, в каждой строке будет сумма, равная 15. Аналогично и в каждом столбце будет сумма, равная 15. Расставим числа:

Испытайте свои знания!

Для самых умных и талантливых учеников мы проводим на сайте дистанционную интернет-олимпиаду. Сразу же после прохождения олимпиады показываются результаты и полный разбор задач для работы над ошибками. В зависимости от успехов олимпиадника выдаются электронные дипломы и похвальные грамоты.

Каждый участник получает электронный сертификат участника.

Источник