Конспект урока способы задания функции 10 класс

Открытый урок по теме: «Функция: понятие, способы задания, основные характеристики. Обратная функция. Суперпозиция функций».
план-конспект урока по алгебре (10 класс) по теме

Изложены основные характеристики функции. Приведены определения обратной функции и сложной функции.

Скачать:

Вложение	Размер
основные свойства функций	191.5 КБ

Предварительный просмотр:

Тема: «Функция: понятие, способы задания, основные характеристики. Обратная функция. Суперпозиция функций».

«Изучать что-либо и не задумываться над

выученным — абсолютно бесполезно.

Задумываться над чем-либо, не изучив

предварительно предмет раздумий-

Цель и психолого-педагогические задачи урока :

1. Общеобразовательная (нормативная) цель : повторить со студентами определение и свойства функции. Ввести понятие суперпозиции функций.
2. Задачи математического развития студентов : на нестандартном учебно-математическом материале продолжить развитие ментального опыта учащихся, содержательной когнитивной структуры их математического интеллекта, в том числе, способностей к логико-дедуктивному и индуктивному, аналитическому и синтетическому обратимому мышлению, к алгебраическому и образно-графическому мышлению, к содержательному обобщению и конкретизации, к рефлексии и самостоятельности как метакогнитивной способности студентов; продолжить развитие культуры письменной и устной речи как психологических механизмов учебно-математического интеллекта.
3. Воспитательные задачи : продолжить личностное воспитание у студентов познавательного интереса к математике, ответственности, чувства долга, академической самостоятельности, коммуникативного умения сотрудничать с группой, преподавателем, согруппниками; аутогогической способности к соревновательной учебно-математической деятельности, стремления к высоким и высшим ее результатам (акмеический мотив).

Тип урока : изучение нового материала; по критерию ведущего математического содержания — урок-практикум; по критерию типа информационного взаимодействия учащихся и преподавателя – урок сотрудничества.

1) Кудрявцев Л.Д. Курс математического анализа: Учеб. для студентов университетов и вузов. В 3 т. Т. 3. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1989. – 352 с. : ил.

2) Демидович Б.П. Сборник задач и упражнений по математическому анализу. – 9-е изд. – М.: Издательство «Наука», 1977.

1.Объявление темы и главной образовательной цели урока; стимулирование чувства долга, ответственности, познавательного интереса студентов при подготовке к сессии.

2.Повторение материала по вопросам.

a) Дать определение функции.

Одним из основных математических понятий является понятие функции. Понятие функции связано с установлением зависимости между элементами двух множеств.

Пусть даны два непустых множества и . Соответствие f, которое каждому элементу сопоставляет один и только один элемент , называется функцией и записывается y = f(x). Говорят еще, что функция f отображает множество на множество .

Например, соответствия f и g, изображенные на рис.1 а и б, являются функциями, а на рис.1 в и г – нет. В случае в – не каждому элементу соответствует элемент . В случае г не соблюдается условие однозначности.

Множество X называется областью определения функции f и обозначается D(f) . Множество всех называется множеством значений функции f и обозначается E(f).

б) Числовые функции. График функции. Способы задания функций.

Пусть задана функция .

Если элементами множеств и являются действительные числа, то функцию f называют числовой функцией . Переменная x при этом называется аргументом или независимой переменной, а y – функцией или зависимой переменной (от x). Относительно самих величин x и y говорят, что они находятся в функциональной зависимости .

Графиком функции y = f(x) называется множество всех точек плоскости Oxy , для каждой из которых x является значением аргумента, а y – соответствующим значением функции.

Чтобы задать функцию y = f(x), необходимо указать правило, позволяющее, зная x , находить соответствующее значение y.

Наиболее часто встречаются три способа задания функции: аналитический, табличный, графический.

Аналитический способ : функция задается в виде одной или нескольких формул или уравнений.

Если область определения функции y = f(x) не указана, то предполагается, что она совпадает с множеством всех значений аргумента, при которых соответствующая формула имеет смысл.

Аналитический способ задания функции является наиболее совершенным, так как к нему приложены методы математического анализа, позволяющие полностью исследовать функцию y = f(x).

Графический способ : задается график функции.

Преимуществом графического задания является его наглядность, недостатком – его неточность.

Табличный способ : функция задается таблицей ряда значений аргумента и соответствующих значений функции. Например, известные таблицы значений тригонометрических функций, логарифмические таблицы.

в) Основные характеристики функции.

1. Функция y = f(x),определенная на множестве D, называется четной , если выполняются условия и f(-x) = f(x); нечетной , если выполняются условия и f(-x) = -f(x).

График четной функции симметричен относительно оси Oy, а нечетной – относительно начала координат. Например, – четные функции; а y = sinx, – нечетные; y = x-1, – функции общего вида, т.е. не четные и не нечетные.

2.Пусть функция y = f(x) определена на множестве D и пусть . Если для любых значений аргументов из неравенства вытекает неравенство: , то функция называется возрастающей на множестве ; если , то функция называется неубывающей на ; то функция наз. убывающей на ; — невозрастающей .

Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными . Интервалы, в которых функция монотонна, называются интервалами монотонности .

3. Функция y = f(x), определенная на множестве D, называется периодической с периодом T>0, если при каждом x D значение (x+T) D и выполняется равенство f(x+T) = f(x).

Для построения графика периодической функции периода T достаточно построить его на любом отрезке длины T и периодически продолжить его во всю область определения.

Отметим основные свойства периодической функции.

1) Алгебраическая сумма периодических функций, имеющих один и тот же период T, есть периодическая функция с периодом T.

2) Если функция f(x) имеет период T, то функция f(ax) имеет период T/a.

г) Обратная функция.

Пусть задана функция y = f(x) с областью определения D и множеством значений E. Если каждому значению соответствует единственное значение , то определена функция x = z(y) с областью определения E и множеством значений D. Такая функция z(y) называется обратной к функции f(x) и записывается в следующем виде: . Про функции y = f(x) и x = z(y) говорят, что они являются взаимно обратными. Чтобы найти функцию x = z(y), обратную к функции y = f(x), достаточно решить уравнение f(x) = y относительно x.

1. Для функции y = 2x обратной функцией является функция x = ½ y;
2. Для функции обратной функцией является функция .

Из определения обратной функции вытекает, что функция y = f(x) имеет обратную тогда и только тогда, когда f(x) задает взаимно однозначное соответствие между множествами D и E. Отсюда следует, что любая строго монотонная функция имеет обратную . При этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).

1. Изучение нового материала.

Пусть функция y = f(u) определена на множестве D, а функция u = z(x) на множестве , причем для соответствующее значение . Тогда на множестве определена функция u = f(z(x)), которая называется сложной функцией от x (или суперпозицией заданных функций, или функцией от функции ).

Переменную u = z(x) называют промежуточным аргументом сложной функции.

Например, функция y = sin2x есть суперпозиция двух функций y = sinu и u = 2x. Сложная функция может иметь несколько промежуточных аргументов.

4. Решение нескольких примеров у доски.

5. Заключение урока.

1) теоретико-прикладные итоги практического занятия; дифференцированная оценка уровня ментального опыта учащихся; уровня усвоения ими темы, компетентности, качества устной и письменной математической речи; уровня проявленного творчества; уровня самостоятельности и рефлексии; уровня инициативы, познавательного интереса к отдельным методам математического мышления; уровней сотрудничества, интеллектуальной состязательности, стремления к высоким показателям учебно-математической деятельности и др.;

2) объявление аргументированных отметок, поурочного балла.

Источник

Урок алгебры в 10 классе по теме «Понятие функции и ее графика»

Муниципальное бюджетное общеобразовательное учреждение

«Средняя общеобразовательная школа №7» города Губкина

по алгебре и началам математического анализа

«Понятие функции и ее графика»

Провела: ________/Соловцова В.В./

Урок алгебры и начал математического анализа

по теме «Понятие функции и ее графика»

Тип урока : введение нового материала.

Ввести и закрепить определения функции, области определения функции и графика функции.

Обогатить опыт учащихся в получении новых знаний на основе уже имеющихся теоретических знаний, а также через использование знакомых ситуаций практического характера.

Развивать логическое мышление учащихся через формирование умения строить графики функций.

Воспитывать графическую культуру учащихся.

Оборудование: учебное пособие «Алгебра и начала математического анализа. 10 класс (профильный уровень)» С.М, Никольский и др. Таблицы числовых функций. Презентация к уроку.

Сообщение темы урока; постановка цели урока; сообщение этапов урока.

Повторить ранее изученный материал: определение функции; способы задания; область определения и область значений; графики функций.

Изучение нового материала

История возникновения понятия функции, примеры функций; первые определения функции, использование графического способа заданий функции.

Закрепление изученного материала

Первичное закрепление полученных знаний.

Обобщение знаний, полученных на уроке.

Инструктаж по домашнему заданию.

I. Организационный момент. (слайд 1).

Учитель сообщает учащимся тему и цель урока и средства ее достижения. ( слайды 2,3,4)

В различных сферах жизни мы нередко имеем дело со всевозможными соответствиями, т.е. правилами, по которым одним объектам (элементам) сопоставляются другие. Изучение явлений реального мира показывает, что переменные величины не изменяются независимо друг от друга; изменение числовых значений одних влечет изменение других.

Учащиеся приводят примеры.

Вопрос. Как называются такие соответствия между элементами?

Вспомнить: 1) определение функции (слайд 5),

2) способы задания функции (слайд 6),

3) что называется областью определения функции? Областью значений функции? (слайд 7-8),

4) Что называется графиком функции?

5) Какие из данных графиков являются графиками некоторых функций? (слайд 9).

6) С графиками каких функций мы знакомы? (слайд 10-14).

Физминутка для глаз. (слайд 15).

Ученики слушают музыку и глазами следят за движущимися объектами, при мигании моргают глазами.

ΙΙΙ Изучение нового материала.

История возникновения понятия функции. (слайд 16)

Понятие функции уходит своими корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Исследования общих зависимостей началось в 14 веке. Функция – основное понятие математического анализа. Но в начале оно было расплывчатым, не имело сколько — нибудь точного описания. Термин «функция» ввел в математику Готфрид Лейбниц. Он употреблял его в очень узком смысле, связывая только с геометрическими образами. Лишь И.Бернулли дал определение функции, свободное от геометрического языка. Наиболее точное определение было предложено великим русским математиком Н.И.Лобачевским и немецким математиком Дирихле.

2.Примеры функций: ( прочитать по учебнику стр.94)

3.Использование графического способа заданий функции. (слайд 17).

Графический способ – один из самых удобных и наглядных способов представления и анализа информации. Его используют метеорологи, отмечая температуру с помощью термографа; сейсмографы, фиксируя колебания почвы; врачи, выявляя болезни сердца с помощью кардиографа; экономисты, рассчитывая спрос и предложения, линии производственных возможностей.

ΙΥ. Закрепление изученного материала.

Учебник стр.96 №3.4; №3.5(а,б,в,г) (слайд 18)

Какое соответствие называется функцией?

Что такое область определения Х функции?

Дайте определение графика функции.

ΥΙ. Домашнее задание: п.3.1; №3.3(а,б,в), на повторение №2.96(а). (слайд 19).

Источник

Числовые функции. Определение и способы задания

Урок 1. Алгебра 10 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Числовые функции. Определение и способы задания»

· повторить определение числовых функций;

· повторить способы задания функций;

· повторить основные преобразования графиков числовых функций;

· повторить вид графиков основных функций.

Если даны числовое множество X и правило f, которое позволяет поставить в соответствие каждому элементу x из множества X определенное число y, то говорят, что задана функция y=f(x) с областью определения X.

x – независимая переменная или аргумент.

y – зависимая переменная.

Множество всех значений y=f(x), где x принадлежит множеству X называют областью значений функции и обозначают E(f).

Если дана функция y=f(x), где x принадлежит множеству X и на координатной плоскости отмечены все точки вида (x, y), где x принадлежит множеству X, а y=f(x), то множество этих точек называют графиком функции y=f(x), где x принадлежит множеству X.

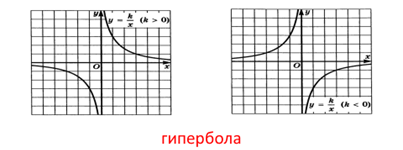
Перед вами графики некоторых функций и их названия.

Зная график функции f(x) с помощью геометрических преобразований можно построить график функции y=f(x+a)+b. Для этого надо сделать параллельный перенос графика функции f(x) на вектор (-a;b), то есть на │a│ вправо, если a 0 на │b│ вверх, если b>0, и вниз, если b Оцените видеоурок

Источник

Читайте также:  Соединение проводов способы соединения проводов технология соединения проводов