Конечные автоматы способы задания конечных автоматов

1. Понятие конечного автомата

Теория автоматов представляет собой раздел дискретной математики, изучающий модели преобразователей дискретной информации. Такими преобразователями являются как реальные устройства (компьютеры, живые организмы), так и воображаемые устройства (аксиоматические теории, математические машины). По сути конечный автомат можно охарактеризовать как устройство М, имеющее входной и выходной каналы при этом в каждый из дискретных моментов времени, называемых тактовыми моментами, оно находится в одном из конечных состояний.

По входному каналу в каждый момент времени t=1, 2, . в устройство М поступают входные сигналы (из некоторого конечного множества сигналов). Задается закон изменения состояния к следующему моменту времени в зависимости от входного сигнала и состояния устройства в текущий момент времени. Выходной сигнал зависит от состояния и входного сигнала в текущий момент времени (рис. 1).

Конечный автомат является математической моделью реальных дискретных устройств по переработке информации.

множество X=<a₁, . a_m> называется входным алфавитом, а его элементы — входными сигналами, их последовательности — входными словами;

множество Y=<b₁, . b_p> называется выходным алфавитом, его элементы — выходными сигналами, их последовательности — выходными словами;

С конечным автоматом ассоциируется воображаемое устройство, ко­торое работает следующим образом. Оно может находиться в состоянии из множества Q, воспринимать сигналы из множества X и выдавать сигналы из множества Y.

2. Способы задания конечного автомата

Существует несколько эквивалентных способов задания абстрактных автоматов, среди которых можно назвать три: табличный, геометрический и функциональный.

Источник

Теория вычислений. Введение в конечные автоматы

Это до предела упрощенная модель компьютера имеющая конечное число состояний, которая жертвует всеми особенностями компьютеров такие как ОЗУ, постоянная память, устройства ввода-вывода и процессорными ядрами в обмен на простоту понимания, удобство рас­суждения и легкость программной или аппаратной реализации.

С помощью КА можно реализовать такие вещи как, регулярные выражения, лексический анализатор, ИИ в играх и тд.

У конечных автоматов имеется таблица переходов, текущее состояние автомата, стартовое состояние и заключительное состояние.

Таблица переходов — В ней хранятся переходы для текущего состояния и входного символа. Простейшая реализация может быть как двумерный массив.

• По горизонтали вверху находятся возможные входные символы.
• По вертикали слева находятся текущие возможные состояния.

Здесь видно, что из состояния 0 в состояние 1 можно попасть только, если у нас будет входной символ ‘a’, из состояния 1 в состояние 2, если символ ‘b’.

Текущее состояние — множество состояний в котором автомат может находиться в данный момент времени.

Стартовое состояние — состояние откуда КА начинает свою работу.

Заключительное состояние — множество состояний в которых автомат принимает определенную цепочку символов, в ином случае отвергает.

Детерминированные конечные автоматы (deterministic finite automaton)

Простейший КА, в котором может быть одно состояние в текущий момент времени, обладает детерминированностью.

Детерминированность — для всех состояний имеется максимум и минимум одно правило для любого возможного входного символа, то есть например, для состояния 1 не может быть два перехода с одним и тем же входным символом.

Недетерминированные конечные автоматы (nondeterministic finite automaton)

НКА не является каким-то существенным улучшением ДКА, просто в нем добавлен так сказать синтаксический сахар, в виде свободных переходов, недетерминированности и множеств состояний. Реализовать можно как массив состоящий из структур в которой хранится состояние, входной символ и следующее состояние.

Свободные переходы (эпсилон переходы) — переходы, которые можно совершать без чтения входного символа.

Недетерминированность — ноль и более переходов для одного символа в каких-либо состояниях.

Множества состояний — в один момент времени НКА может находится в нескольких состояниях.

Заключительное состояние обозначается двойным кругом.

В стартовом состоянии у нас текущим состоянием является <1>, при входном символе ‘b’ у нас появляется возможность, пойти в состояние 1 и в состояние 2, то есть после входного символа ‘b’ текущим состоянием является множество <1, 2>.

Свободным переходом обозначается пунктирной линией.

Здесь видно два свободных перехода из стартового состояния, то есть без чтения входного символа мы сразу находимся в множестве состоянии <2, 4>.

Для преобразования НКА в ДКА используется алгоритм Томпсона.
При преобразовании НКА в ДКА может получиться не совсем минимальный ДКА и для его минимизации можно применить алгоритм Бржозовского.

Конечные автоматы с магазинной памятью (pushdown automaton)

Это тот же КА, но с дополнительной памятью в виде стека. Теперь для совершения перехода нужно учитывать еще несколько факторов, символ который нужно удалить из стека и символы которые нужно добавить в стек.

КАМП можно применять в таких местах, где может быть неограниченное количество вложений, например при разборе языков программирование или подсчету вложенных скобок в математических выражениях. Реализовать с помощью КА невозможно, ведь количество возможных состояний конечно в отличие от стека (я понимаю, что память тоже конечна).

Удаление символа из стека — при любом переходе решается какой символ вытолкнуть, если на вершине стека не оказалось такого символа, то он и не выталкивается. Так же если символ нужно оставить в стеке, то он добавляется вместе с добавляемыми символами.

Добавление символов в стек — при любом переходе решает какие символы добавить в стек.

• Детерминированные — к нему применяются те же правила как к ДКА к тому же завершает работу только в заключительном состоянии.
• Недетерминированные — к нему применяются те же правила как к НКА к тому же он может завершать работу в заключительном состоянии или когда стек станет пуст.

Шаблон: входной_символ; удаляемый_символ/добавляемый символ. На дно стека добавляется символ $ для, того, что понять когда он закончился.

Этот КАМП подсчитывает вложенность скобок, за счет добавления и удаления символов из стека.

ДАМП не равен НАМП, поэтому невозможно одно преобразовать в другое, следовательно НАМП обладает преимуществом перед ДАМП.

Машина Тьюринга (Turing machine)

Самая мощная машина из существующих, его преимущество перед другими в ленте с которой он может работать как хочет. В нем нет свободных переходов. Умеет интерпретировать другие автоматы такие как КА, КАМП.

Лента — это одномерный массив в который могут записываться данные за счет головки над ячейкой, который можно заранее заполнить входными данными.

Шаблон: считаный_символ_с_головки/записаный_символ; сторона_смещения_головки. края ленты обозначаются ‘_’.

Эта МТ выполняет инкремент двоичного числа, головка стоит слева, там где начинается лента.

1. Если находится в состоянии 1 и прочитан нуль, записать еди­ницу, сдвинуть вправо и перейти в состояние 2.
2. Если находится в состоянии 1 и прочитана единица, записать нуль, сдвинуть влево и перейти в состояние 1.
3. Еcли находится в состоянии 1 и прочитан пустой квадратик, записать единицу, сдвинуть вправо и перейти в состояние 2.
4. Если находится в состоянии 2 и прочитан нуль, записать нуль, сдвинуть вправо и остаться в состояние 2.
5. Если находится в состоянии 2 и прочитана единица, записать единицу, сдвинуть вправо и остаться в состояние 2.
6. Если находится в состоянии 2 и прочитать пустой квадратик, записать пустой квадратик, сдвинуть влево и перейти в состоя­ние 3.

ДМТ эквивалентен НМТ, так, что они тоже не различаются.

Универсальная машина Тьюринга (universal Turing machine)

Машина которая может порождать другие машины Тьюринга, получая на входную ленту данные машины.

1. Память порождаемой машины не может быть больше, чем у самой УМТ.
2. Нужно уметь правильно разделять пространство ленты между порождаемой машиной и УМТ, ведь их данные находятся на одной ленте.

На этом введение в автоматы закончено, теперь вы можете продолжить изучать дальнейший материал сами.

Источник

Способы задания конечных автоматов

Представление конечного автомата фактически сводится к описанию задающих его автоматных функций. [8]

Существуют три способа задания конечных автоматов:

· Табличный (матрицы переходов и выходов);

· Графический (с помощью графов);

· Аналитический (с помощью формул).

Аналитический способ – автомат задаетсясистемой уравнений. Из такой системы следует, что при конечном числе возможных внутренних состояний количество возможных значений автоматных функций также оказывается конечным. Примером такого задания служат системы уравнений, задающие автоматы Мили и автоматы Мура

Табличный способ.Составляется таблица состояния автоматадля функции перехода – δ и функции выхода. При этом:

· столбцы таблицы соответствуют элементам входного алфавита X,

· строки таблицы соответствуют состояни­ям (элементы конечного множества Q).

Пересечению i-и строки и j-го столбца соответствует клетка (i, j), которая является аргументом функций 8 и λ автомата в момент, когда он находится в состоя­нии q_i на его входе – слово x_j, а в самой соответствующей клетке запишем значения функций 8 и λ. Таким образом, вся таблица соответствует множеству Q х X.

При заполнении таблицы переходов каждая клеточка однознач­но определяется парой символов: символом следующего состоя­ния и символом выходного сигнала.

На практике автоматные функции задаются двумя конечными таблицами, именуемыми соответственно матрицей перехода и матрицей выводов. При этом строки обозначаются буквами входного алфавита, а столбцы буквами внутреннего алфавита (символами, кодирующими внутреннее состояние автомата).

В матрице переходов на пересечении строки x_k и столбца q_r помещается значение функции перехода δ(q_i, х) и функции выводов λ(q, х). В ряде случаев обе таблицы объединяются в одну таблицу.

Графический способ.

Автомат задается с помощью графа, схемы, графика и др. Задание с помощью ориентированного гра­фа – более удобная и компактная форма описания автомата.

Граф автомата содержит

· Вершины, соответствующие состоянию q_iÎQ,

· Дуги, соединяющие вершины – переходы автомата из одного состояния в другое. На дугах принято указывать пары вход­ных и выходных сигналов – сигналов переходов.

Если автомат переходит из состояния q₁ в состояние q₂ под воз­действием нескольких входных сигналов, то на соответствующей дуге графа этот вариант будет представлен через дизъюнкцию. Для представления автомата используют двухполюсные графы с выде­ленными начальным и конечным состояниями.

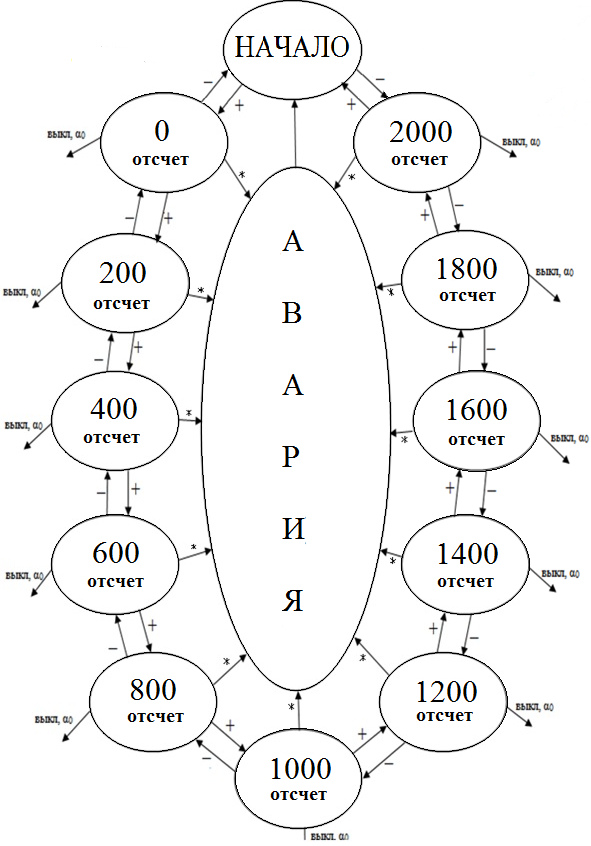
Разработка шкалы «прибора для измерения емкости»

№	индикация	+	—	перегруз.	выкл.	┤
0	исх.сост.	1	0	0	0	нет
1	0	2	0	13	0	да
2	50	3	1	13	0	да
3	100	4	2	13	0	да
4	150	5	3	13	0	да
5	200	6	4	13	0	да
6	250	7	5	13	0	да
7	300	8	6	13	0	да
8	350	9	7	13	0	да
9	400	10	8	13	0	да
10	450	11	9	13	0	да
11	500	13	10	13	0	да
12	ОВ	0	0	0	0	нет
13	авария	0	0	0	0	нет

Рис.2.5. Граф шкалы прибора для измерения емкости

Заключение

Поскольку применение генераторов с колебательными контурами (типа RC) для генерирования колебаний высокой частоты не удовлетворяет, для разрабатываемого генератора была взята схема типа LC (в качестве фазирующей цепочки взята трехточечная схема с автотрансформаторной связью, активный элемент — транзистор).

В теоретической части данной курсовой работы были рассмотрены элементы генераторов LC-типа. Также была рассмотрена классификация генераторов LC-типа, их назначение, а также различные схемы генераторов. А также технические характеристики элементов генераторов.

В практической части была раскрыта тема, касающаяся шифраторов, дешифраторов, их назначения, а также были спроектированы электрические функциональные и электрические принципиальные схемы шифраторов и дешифраторов. Была раскрыта тема карт Карно. Также был разработан сегмент “b” семисегментного индикатора. Был разработан конечный автомат для шкалы прибора для измерения емкости, а также граф для него.

Дата добавления: 2018-02-18 ; просмотров: 2767 ; Мы поможем в написании вашей работы!

Источник