Компрессия данных с помощью алгоритма хаффмана способ реализации свойства

Содержание

Алгоритм Хаффмана
Содержание
Определение [ править ]
Алгоритм построения бинарного кода Хаффмана [ править ]
Время работы [ править ]
Пример [ править ]
Корректность алгоритма Хаффмана [ править ]
Сжатие данных алгоритмом Хаффмана
Вступление
Немного размышлений
Кодирование
Построение дерева Хаффмана
А что дальше?
Декодирование
Реализация
Заключение
Благодарности

Алгоритм Хаффмана

Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.

Содержание

Определение [ править ]

Определение:

Пусть [math]A=\,a_<2>, \ldots ,a_\>[/math] — алфавит из [math]n[/math] различных символов, [math]W=\,w_<2>, \ldots ,w_\>[/math] — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов [math]C=\,c_<2>, \ldots ,c_\>[/math] , где [math]c_[/math] является кодом для символа [math]a_[/math] , такой, что:

[math]c_[/math] не является префиксом для [math]c_[/math] , при [math]i \ne j[/math] ,

cумма [math]\sum\limits_ w_\cdot |c_|[/math] минимальна ( [math]|c_|[/math] — длина кода [math]c_[/math] ),

называется кодом Хаффмана.

Алгоритм построения бинарного кода Хаффмана [ править ]

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
Из списка выберем два узла с наименьшим весом.
Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
Добавим к списку только что сформированный узел вместо двух объединенных узлов.
Если в списке больше одного узла, то повторим пункты со второго по пятый.

Время работы [ править ]

Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время [math]O(N \log N)[/math] .Такую асимптотику можно улучшить до [math]O(N)[/math] , используя обычные массивы.

Пример [ править ]

Закодируем слово [math]abracadabra[/math] . Тогда алфавит будет [math]A= \ [/math] , а набор весов (частота появления символов алфавита в кодируемом слове) [math]W=\<5, 2, 2, 1, 1\>[/math] :

В дереве Хаффмана будет [math]5[/math] узлов:

Узел	a	b	r	с	d
Вес	5	2	2	1	1

По алгоритму возьмем два символа с наименьшей частотой — это [math]c[/math] и [math]d[/math] . Сформируем из них новый узел [math]cd[/math] весом [math]2[/math] и добавим его к списку узлов:

Узел	a	b	r	cd
Вес	5	2	2	2

Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :

Узел	a	rcd	b
Вес	5	4	2

Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :

Узел	brcd	a
Вес	6	5

На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :

Узел	abrcd
Вес	11

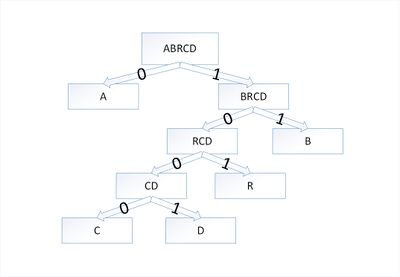
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):

Символ	a	b	r	с	d
Код	0	11	101	1000	1001

Таким образом, закодированное слово [math]abracadabra[/math] будет выглядеть как [math]01110101000010010111010[/math] . Длина закодированного слова — [math]23[/math] бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы [math]33[/math] бита, что существенно больше.

Корректность алгоритма Хаффмана [ править ]

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Доказательство: [math]\triangleright[/math]

Возьмем дерево [math]T[/math] , представляющее произвольный оптимальный префиксный код для алфавита [math]C[/math] . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] — листья с общим родительским узлом, находящиеся на максимальной глубине.

Пусть символы [math]a[/math] и [math]b[/math] имеют общий родительский узел и находятся на максимальной глубине дерева [math]T[/math] . Предположим, что [math]f[a] \leqslant f[b][/math] и [math]f[x] \leqslant f[y][/math] . Так как [math]f[x][/math] и [math]f[y][/math] — две наименьшие частоты, а [math]f[a][/math] и [math]f[b][/math] — две произвольные частоты, то выполняются отношения [math]f[x] \leqslant f[a][/math] и [math]f[y] \leqslant f[b][/math] . Пусть дерево [math]T'[/math] — дерево, полученное из [math]T[/math] путем перестановки листьев [math]a[/math] и [math]x[/math] , а дерево [math]T»[/math] — дерево полученное из [math]T'[/math] перестановкой листьев [math]b[/math] и [math]y[/math] . Разность стоимостей деревьев [math]T[/math] и [math]T'[/math] равна:

[math]B(T) — B(T’) = \sum\limits_ f(c)d_T(c) — \sum\limits_ f(c)d_(c) = (f[a] — f[x])(d_T(a) — d_T(x)),[/math]

что больше либо равно [math]0[/math] , так как величины [math]f[a] — f[x][/math] и [math]d_T(a) — d_T(x)[/math] неотрицательны. Величина [math]f[a] — f[x][/math] неотрицательна, потому что [math]x[/math] — лист с минимальной частотой, а величина [math]d_T(a) — d_T(x)[/math] является неотрицательной, так как лист [math]a[/math] находится на максимальной глубине в дереве [math]T[/math] . Точно так же перестановка листьев [math]y[/math] и [math]b[/math] не будет приводить к увеличению стоимости. Таким образом, разность [math]B(T’) — B(T»)[/math] тоже будет неотрицательной.

Таким образом, выполняется неравенство [math]B(T») \leqslant B(T)[/math] . С другой стороны, [math]T[/math] — оптимальное дерево, поэтому должно выполняться неравенство [math]B(T) \leqslant B(T»)[/math] . Отсюда следует, что [math]B(T) = B(T»)[/math] . Значит, [math]T»[/math] — дерево, представляющее оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] имеют одинаковую максимальную длину, что и доказывает лемму. [math]\triangleleft[/math]

Лемма (2):

Доказательство:

[math]\triangleright[/math]

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] может быть выражена через стоимость [math]B(T’)[/math] дерева [math]T'[/math] . Для каждого символа [math]c \in C \backslash \[/math] верно [math]d_T(C) = d_[/math] , значит, [math]f[c]d_T(c) = f[c]d_(c)[/math] . Так как [math]d_T(x) = d_T(y) = d_ (z) + 1[/math] , то

[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_(z) + 1) = f[z]d_(z) + (f[x] + f[y])[/math]

из чего следует, что

[math] B(T) = B(T’) + f[x] + f[y] [/math]

[math] B(T’) = B(T) — f[x] — f[y] [/math]

Докажем лемму от противного. Предположим, что дерево [math]T[/math] не представляет оптимальный префиксный код для алфавита [math]C[/math] . Тогда существует дерево [math]T»[/math] такое, что [math]B(T») \lt B(T)[/math] . Согласно лемме (1), элементы [math]x[/math] и [math]y[/math] можно считать дочерними элементами одного узла. Пусть дерево [math]T»'[/math] получено из дерева [math]T»[/math] заменой элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y][/math] . Тогда

[math]B(T»’) = B(T») — f[x] — f[y] \lt B(T) — f[x] — f[y] = B(T’)[/math] ,

Источник

Сжатие данных алгоритмом Хаффмана

Вступление

В данной статье я расскажу вам о широко известном алгоритме Хаффмана, и вы наконец разберетесь, как все там устроено изнутри. После прочтения вы сможете своими руками(а главное, головой) написать архиватор, сжимающий реальные, черт подери, данные! Кто знает, быть может именно вам светит стать следующим Ричардом Хендриксом!

Да-да, об этом уже была статья на Хабре, но без практической реализации. Здесь же мы сфокусируемся как на теоретической части, так и на программерской. Итак, все под кат!

Немного размышлений

В обычном текстовом файле один символ кодируется 8 битами(кодировка ASCII) или 16(кодировка Unicode). Далее будем рассматривать кодировку ASCII. Для примера возьмем строку s1 = «SUSIE SAYS IT IS EASY\n». Всего в строке 22 символа, естественно, включая пробелы и символ перехода на новую строку — ‘\n’. Файл, содержащий данную строку будет весить 22*8 = 176 бит. Сразу же встает вопрос: рационально ли использовать все 8 бит для кодировки 1 символа? Мы ведь используем не все символы кодировки ASCII. Даже если бы и использовали, рациональней было бы самой частой букве — S — дать самый короткий возможный код, а для самой редкой букве — T (или U, или ‘\n’) — дать код подлиннее. В этом и заключается алгоритм Хаффмана: необходимо найти оптимальный вариант кодировки, при котором файл будет минимального веса. Вполне нормально, что у разных символов длины кода будут отличаться — на этом и основан алгоритм.

Кодирование

Почему бы символу ‘S’ не дать код, например, длиной в 1 бит: 0 или 1. Пусть это будет 1. Тогда второму наиболее встречающемуся символу — ‘ ‘(пробел) — дадим 0. Представьте себе, вы начали декодировать свое сообщение — закодированную строку s1 — и видите, что код начинается с 1. Итак, что же делать: это символ S, или же это какой-то другой символ, например A? Поэтому возникает важное правило:

Ни один код не должен быть префиксом другого

Это правило является ключевым в алгоритме. Поэтому создание кода начинается с частотной таблицы, в которой указана частота (количество вхождений) каждого символа:

Символы с наибольшим количеством вхождений должны кодироваться наименьшим возможным количеством битов. Приведу пример одной из возможных таблиц кодов:

Таким образом, закодированное сообщение будет выглядеть так:

Код каждого символа я разделил пробелом. По-настоящему в сжатом файле такого не будет!
Вытекает вопрос: ~~как этот салага придумал код~~ как создать таблицу кодов? Об этом пойдет речь ниже.

Построение дерева Хаффмана

Здесь приходят на выручку бинарные деревья поиска. Не волнуйтесь, здесь методы поиска, вставки и удаления не потребуются. Вот структура дерева на java:

Это не полный код, полный код будет ниже.

Вот сам алгоритм построения дерева:

Создать объект Node для каждого символа из сообщения(строка s1). В нашем случае будет 9 узлов(объектов Node). Каждый узел состоит из двух полей данных: символ и частота
Создать объект Дерева(BinaryTree) для кажлого из узлов Node. Узел становится корнем дерева.
Вставить эти деревья в приоритетную очередь. Чем меньше частота, тем больше приоритет. Таким образом, при извлечении всегда выбирается дерево наименьшей частотой.

Далее нужно циклически делать следующее:

Извлечь два дерева из приоритетной очереди и сделать их потомками нового узла (только что созданного узла без буквы). Частота нового узла равна сумме частот двух деревьев-потомков.
Для этого узла создать дерево с корнем в данном узле. Вставить это дерево обратно в приоритетную очередь. (Так как у дерева новая частота, то скорее всего она встанет на новое место в очереди)
Продолжать выполнение шагов 1 и 2, пока в очереди не останется одно дерево — дерево Хаффмана

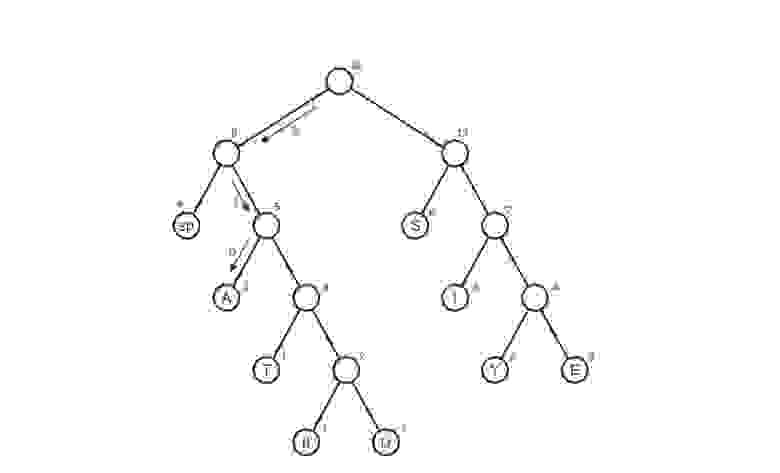
Рассмотрим данный алгоритм на строке s1:

Здесь символ «lf»(linefeed) обозначает переход на новую строку, «sp» (space) — это пробел.

А что дальше?

Мы получили дерево Хаффмана. Ну окей. И что с ним делать? ~~Его и за бесплатно не возьмут~~ А далее, нужно отследить все возможные пути от корня до листов дерева. Условимся обозначить ребро 0, если оно ведет к левому потомку и 1 — если к правому. Строго говоря, в данных обозначениях, код символа — это путь от корня дерева до листа, содержащего этот самый символ.

Таким макаром и получилась таблица кодов. Заметим, что если рассмотреть эту таблицу, то можно сделать вывод о «весе» каждого символа — это длина его кода. Тогда в сжатом виде исходный файл будет весить: 2 * 3 + 2*4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 бит. Вначале он весил 176 бит. Следовательно, мы уменьшили его аж в 176/65 = 2.7 раза! Но это утопия. Такой коэффициент вряд ли будет получен. Почему? Об этом пойдет речь чуть позже.

Декодирование

Ну, пожалуй, осталось самое простое — декодирование. Я думаю, многие из вас догадались, что просто создать сжатый файл без каких-либо намеков на то, как он был закодирован, нельзя — мы не сможем его декодировать! Да-да, мне было тяжело это осознать, но придется создать текстовый файл table.txt с таблицей сжатия:

Запись таблицы в виде ‘символ’«код символа». Почему 01110 без символа? На самом деле он с символом, просто средства java, используемые мной при выводе в файл, символ перехода на новую строку — ‘\n’ -конвертируют в переход на новую строку(как бы это глупо не звучало). Поэтому пустая строка сверху и есть символ для кода 01110. Для кода 00 символом является пробел в начале строки. Сразу скажу, что ~~нашему коэффициенту хана~~этот способ хранения таблицы может претендовать на самый нерациональный. Но он прост для понимания и реализации. С удовольствием выслушаю Ваши рекомендации в комментариях по поводу оптимизации.

Имея эту таблицу, очень просто декодировать. Вспомним, каким правилом мы руководствовались, при создании кодировки:

Ни один код не должен являться префиксом другого

Вот тут-то оно и играет облегчающую роль. Мы читаем последовательно бит за битом и, как только полученная строка d, состоящая из прочтенных битов, совпадает с кодировкой, соответствующей символу character, мы сразу знаем что был закодирован символ character (и только он!). Далее записываем character в декодировочную строку(строку, содержащую декодированное сообщение), обнуляем строку d, и читаем дальше закодированный файл.

Реализация

Пришло время ~~унижать мой код~~ писать архиватор. Назовем его Compressor.

Начнем с начала. Первым делом пишем класс Node:

Класс, создающий дерево Хаффмана:

Класс, содержащий который кодирует/декодирует:

Класс, облегчающий запись в файл:

Класс, облегчающий чтение из файла:

Ну, и главный класс:

Файл с инструкциями readme.txt предстоит вам написать самим 🙂

Заключение

Наверное, это все что я хотел сказать. Если у вас есть что сказать по поводу ~~моей некомпетентности~~ улучшений в коде, алгоритме, вообще любой оптимизации, то смело пишите. Если я что-то недообъяснил, тоже пишите. Буду рад услышать вас в комментариях!

Да-да, я все еще здесь, ведь я не забыл про коэффициент. Для строки s1 кодировочная таблица весит 48 байт — намного больше исходного файла, да и про добавочные нули не забыли(количество добавленных нулей равно 7)=> коэффициент сжатия будет меньше единицы: 176/(65 + 48*8 + 7)=0.38. Если вы тоже это заметили, то ~~только не по лицу~~ вы молодец. Да, эта реализация будет крайне неэффективной для малых файлов. Но что же происходит с большими файлами? Размеры файла намного превышают размер кодировочной таблицы. Вот здесь-то алгоритм работает как-надо! Например, для монолога Фауста архиватор выдает реальный (не идеализированный) коэффициент, равный 1.46 — почти в полтора раза! И да, предполагалось, что файл будет на английском языке.

Выпустил upgrade: добавил GUI + изменил алгоритм обработки исходного текста так, чтобы не читать весь файл в память. Короче, кидаю ссылку на git для любознательных: сами всё увидите.

Благодарности

Как и автор каждой хорошей книги, я созидал эту статью не без помощи других людей. Имхо, очень мало людей сделало что-то крутое в одиночку.

Огромное спасибо Исаеву Виталию Вячеславовичу за небходимую теоретическую поддержку.
Также, часть материала этой статьи взята из книги Роберта Лафоре «Data Structures and Algorithms in Java». Если сомневаетесь как или окуда начать свой путь в теории алгоритмов и структур данных — берите, не прогадаете.

Источник