13. Перестановки с повторениями
При перестановке букв в слове «толпа» получается P5 = 5! = 120 «слов». Если же переставлять буквы в слове «топот», то получится меньше различных «слов», потому что ни перестановка двух букв «т», ни перестановка двух букв «о» не изменяют «слова»; всего перестановок в данном случае будет 
. Мы имеем здесь дело с перестановками с повторениями.
Общую задачу сформулируем следующим образом.
Имеется n элементов k различных типов: n1 элементов первого типа, n2 элементов второго типа, …, nk элементов k-го типа, 
. Сколько можно составить различных перестановок из этих элементов?
Число перестановок c повторениями обозначают 
. Сколько же их? Если бы все элементы были различны, то число перестановок равнялось бы n!. Но из-за того, что некоторые элементы совпадают, получится меньшее число перестановок. В первой группе элементы (первого типа) можно переставлять друг с другом n1! способами. Но так как все эти элементы одинаковы, то перестановки ничего не меняют. Точно также ничего не меняют n2! перестановок элементов во второй группе и т. д. Перестановки элементов в разных группах можно делать независимо друг от друга. Поэтому (из принципы умножения) элементы можно переставлять друг с другом 
способами так, что она остаётся неизменной.
Число различных перестановок с повторениями, которые можно составить из данных элементов, равно
, (11.1) где 
.
Замечание. Отметим, что формула числа сочетаний из n элементов по k элементов совпадает с формулой для числа перестановок с повторениями из k элементов одного типа и n–k элементов другого типа:
.
Пример 11.1. Сколькими способами можно нанизать на нить 4 зеленых, 5 синих и 6 красных бус?
Решение. Речь идет об отыскании числа перестановок с повторениями, которые можно сделать из k1=4 элементов первого типа (зеленых бус), k2=5 элементов второго типа (синих бус) и k3=6 элементов третьего типа (красных бус). По формуле (6) получаем
.
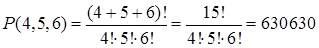
Пример 11.2. У мамы было 2 одинаковых яблока, 3 одинаковых груши и 4 одинаковых апельсина. Каждый день она давала ребенку по одному фрукту. Сколькими способами она могла это сделать?
Решение. Данная задача есть задача на отыскание числа перестановок с повторениями:
.
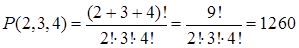
Пример 11.3. Сколько различных браслетов можно сделать из пять одинаковых изумрудов, шести одинаковых рубинов и семи одинаковых сапфиров (в браслет входят все 18 камней)?
Решение. Камни можно переставлять P(5, 6, 7) способами. При циклических перестановках и при зеркальном отражении браслет остается неизменным. В результате получаем
.
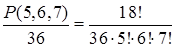
Пример 11.4. Сколько способами можно переставлять буквы слова «огород» так, чтобы: а) три буквы «о» не стояли рядом? б) если запрещается, чтобы две буквы «о» стояли рядом?
Решение. а) Буквы данного слова можно переставлять P(3,1,1,1) способами. Если три буквы «о» стоят рядом, то их можно считать за одну букву. Тогда буквы можно переставлять 4! Способами. Вычитая этот результат из предыдущего, получим
.
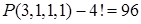
Б) Сначала расставляем согласные (3! способов). Для трёх букв «о» остаётся 4 места, и их можно расставить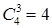 
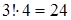
способами. Всего получаем 
способа.
11.1. Сколькими способами можно расположить в ряд две зелёные и четыре красные лампочки?
Ответ: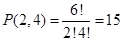 
.
11.2. Десять человек надо разбить на три группы соответственно по 2, 3, 5 человек в группе. Сколькими способами можно это сделать?
Ответ: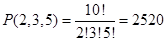 
.
11.3. Сколькими способами можно упаковать девять различных книг в трёх бандеролях соответственно по два три, четыре книги в каждой бандероли?
Ответ: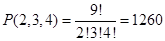 
.
11.4. Группу командировочных из восьми человек требуется расселить в три комнаты, из которых две трёхместные и одна двухместная. Сколько вариантов расселения возможно?
Ответ: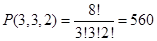 
.
11.5. Сколько различных слов можно получить, переставляя буквы в следующих исходных словах: а) академия, б) электротехника, в) молокопродукт?
Ответ: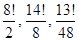 
.
11.6. Сколькими способами можно разделить 12 предметов между тремя студентами, чтобы каждому досталось ровно по четыре предмета?
Ответ: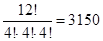 
.
11.7. Для премий на математической олимпиаде выделено 3 экземпляра одной книги, 4 экземпляра другой и 8 экземпляров третьей. Сколькими способами могут быть распределены эти премии между 30 участниками олимпиады, если каждому вручается не более одной книги?
Ответ: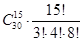 
.
11.8. Сколькими способами можно переставить буквы слова «обороноспособность» так, чтобы две буквы «о» не шли подряд?
Ответ: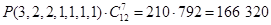 
.
11.9. Сколькими способами можно переставить буквы слова «каракули» так, чтобы никакие две гласные не стояли рядом?
Ответ: Гласные можно переставлять P(2,1,1)=12 способами, Аналогично, P(2,1,1)=12 способами можно расставить согласные буквы. Если согласные уже расставлены, то для гласных останется 5 мест. Поэтому места для них можно выбрать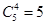 
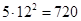
способами. Всего 
способов.
Источник
Комбинаторика с повторениями.
Одна из особенностей комбинаторных задач заключается в том, что в ней исключительно большую роль играет точность формулировки. Обычно в задаче по комбинаторике необходимо определить количество способов или число вариантов какого-либо выбора. Варианты – это умозрительные понятия и их нельзя увидеть непосредственно, если нет полного перечня различных вариантов, описанных с помощью математических символов.
Рассмотрим для примера задачу: определить, сколькими способами можно распределить три конфеты между тремя детьми? Решение зависит от выбранного способа понимания задачи. Источником неопределенности является слово «распределить». Если считать конфеты одинаковыми, то справедливый вариант распределения дает 1 способ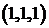 
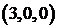
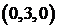
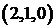
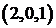
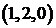
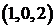
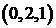
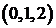
, т.е. каждый ребенок получил по одной конфете. Если же делить не поровну, то возможны варианты распределения: 
, 
, 
, 
, 
, 
, 
, 
, 
. Таким образом, «распределения» дают 10 различных вариантов. Если же дополнительно предположить, что все конфеты различные, то можно получить максимальное число «распределений» — 27 вариантов.
Таким образом, при решении задач важно точно понимать смысл слов «различные варианты». Нужно выяснить, важен ли порядок элементов в выбранном подмножестве, или важен только состав. Кроме того, важно понять, могут ли повторяться элементы, или они берутся в одном экземпляре. Комбинаторные формулы без повторений рассмотрены в §2. В данном параграфе будут рассмотрены формулы и задачи, в которых элементы множества при некотором выборе могут повторяться.
1) Перестановки с повторениями.
Пример 1. Сколькими способами можно переставить буквы в слове «мама»?
Решение. Комбинаторика позволяет считать словом любую комбинацию букв. Если бы в слове «мама» все буквы были бы различными, тогда количество перестановок было бы равно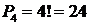 
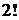
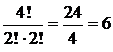
. Но при перестановке двух букв «м» или двух букв «а» будем получать одинаковые буквенные комбинации. Поэтому, их засчитывать не надо. Две буквы «м» можно переставить 
способами. Аналогично для букв «а». В итоге число перестановок букв данного слова без учета повторов окажется равным числу 
. При необходимости все способы можно перебрать.
Замечание. Обычно, если при решении задачи какие-либо варианты не нужно считать, то на это число делят. Этот подход является обратным к правилу умножения.
Перестановки с повторениями используются в тех задачах, в которых речь идёт не о единичных объектах, а о видах, классах, сортах элементов. Понятно, что внутри каждого вида элементы повторяются.
Пусть имеются предметы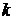 
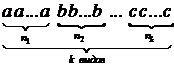
различных типов:
.
Сколькими способами можно переставить местами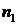 
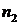
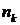
элемент первого вида, 
элементов второго вида, . 
элементов последнего вида?
Общее количество всех элементов в каждой перестановке равно: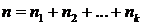 
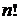
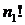
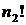
. Перестановки элементов внутри вида не меняет перестановку. Она изменится только в случае межвидовых перестановок. Будем рассуждать аналогично задаче в примере 1. Если бы все элементы были бы различными, то число всех перестановок равнялось бы 
. Но в силу того, что есть повторяющиеся объекты, получится меньшее число перестановок, потому что не нужно считать перестановки элементов первого вида, а их будет 
, не надо засчитывать 
перестановок элементов внутри второго вида и т.д.
Таким образом, число различных перестановок с повторениями находится по формуле:
, где . (1)
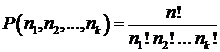
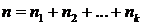
В знаменателе дроби стоят числа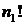 
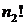
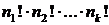
(число перестановок элементов первого вида, которые не нужно засчитывать), 
(число перестановок элементов второго вида) и т. д. Перестановки элементов первого типа, второго типа и т.д. можно делать независимо друг от друга, поэтому по правилу умножения элементы данной перестановки можно переставлять 
способами. Значит, число различных перестановок с повторениями будет равно указанному числу.
Например, перестановки букв в слове «математика» – это перестановки с повторениями. Анаграммы – есть перестановки с повторениями.
Замечание. Дробь, стоящая в правой части формулы (1), является целым числом.
Пример 2. Найти количество анаграмм слова «баобаб».
Решение. Всего – 6 букв. Вхождения букв: «б» — 3 раза, «а» — 2 раза, «о» — 1 раз. Используя формулу (1), имеем:
.
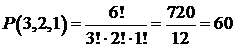
Замечание. Формула для числа перестановок с повторением содержит в себе, как частный случай, формулу для перестановок без повторений (при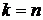 
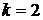
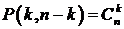
). Кроме того, формула (1) содержит в себе формулу для числа сочетаний (при 
): 
.
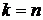
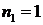
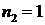
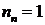
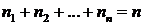
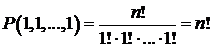
Действительно, если , то тогда 
, 
, …, 
, 
. Значит, 
, т.е. обычные перестановки без повторений – это частный случай перестановок с повторениями.
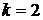
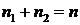
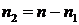
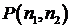
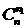
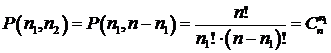
Если , то 
, или 
, тогда по определению 
и 
имеем:
.
Таким образом, если положить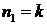 
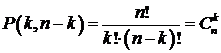
, то последнее равенство примет более естественный для формулы числа сочетаний вид:
.
2) Размещения с повторениями.
Определение размещений с повторениями аналогично определению числа размещений без повторений, но отличается существенно тем, что элементы в подмножествах могут повторяться.
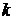
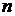
Определение 1: Слова, составленные из букв, которые можно получить из 
повторяющихся букв, называют размещениями с повторениями.
Обозначают: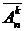 
.
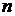
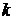
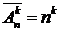
Теорема 1: Число всех размещений из элементов по элементов с повторениями находится по формуле:
. (2)
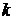
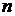
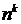
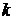
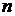
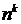
Доказательство. Если имеется упорядоченных мест, для каждого из которых можно выбрать любой из объектов, то согласно комбинаторному принципу умножения, существует 
способов выбора объектов. Таким образом, число перестановок с повторением, когда объектов выбираются из объектов, равно , что и требовалось доказать.
Примеры. 1) Количество телефонных номеров, автомобильных номеров, комбинаций в секретном замке, генетический код. Во всех этих ситуациях в расстановках элементы могут повторяться. Количество комбинаций в секретном замке, число телефонных номеров, число автомобильных номеров, код Морзе, генетический код.
2) Разгадка генетического кода – крупнейшее достижение биологии ХХ века. Информация записана в гигантских молекулах ДНК (дезоксирибонуклеиновой кислоты). Различные молекулы ДНК отличаются порядком 4-х азотистых оснований. Эти основания определяют порядок построения белков организма из двух десятков аминокислот, причём каждая аминокислота зафиксирована кодом из 3-х азотистых оснований.
В одной хромосоме содержится несколько десятков миллионов азотистых оснований. Число различных комбинаций, в которых они могут идти друг за другом столь велико, что ничтожной доли этих комбинаций хватит для зашифровки всего многообразия живых организмов за время существования жизни на земле, оно равно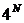 
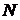
, где 
– число оснований в хромосоме.
3) Пусть имеется множество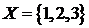 
. Требуется составить его двухэлементные подмножества.
Решение. Если считать, что в этих подмножествах важен только состав, то имеем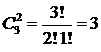 
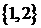
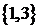
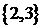
таких подмножества: 
, 
, 
.
Если считать, что в подмножествах важен состав и порядок элементов, то имеем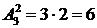 
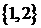
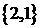
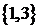
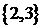
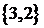
таких подмножеств:
, 
, , 
, , 
.
В таких парах порядок элементов будет важен, если например, речь идет о координатах точек на плоскости.
Если же в построенных подмножествах элементы могут повторяться, то имеем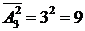 
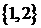
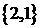
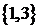
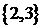
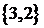
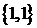
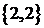
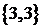
таких подмножеств:
, , , , , , 
, 
, 
.
Замечание. Выше было показано, что перестановки без повторений являются частным случаем размещений без повторений. Для формул с повторениями дело обстоит иначе. Формула числа перестановок с повторениями не является частным случаем формулы числа размещений с повторениями.
Действительно, когда речь идет о повторениях в упорядоченном или неупорядоченном наборе объектов, то возможны две противоположные ситуации:
1) каждый объект должен повторяться в наборе строго заданное число раз;
2) нет никаких ограничений на число повторений объектов, кроме общего их числа в наборе.
В этом отличие перестановок с повторениями и размещений с повторениями. Объединяет их другое – это упорядоченные наборы. Отметим, что для неупорядоченных наборов ситуация с фиксированным набором каждого объекта бессодержательна, поскольку в таком случае это один вариант.
Размещение с повторениями – термин достаточно явный и удобный. В случае «сочетаний с повторениями» с ясностью не все благополучно. Хотя если перестановки и размещения могут быть с повторениями, то имеет смысл поговорить и о сочетаниях с повторениями.
Замечание. Формула для числа перестановок с повторениями не является частным случаем формулы для числа размещений с повторениями. Их может объединять только то, что в обоих случаях имеют место упорядоченные наборы.
3) Сочетания с повторениями.
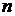
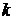
Пусть имеются предметы различных типов. Сколько комбинаций можно сделать из них, если не принимать во внимание порядок элементов? Эту задачу в общем виде можно решать точно так же, как задачу с пирожными.
Пример 3. В кондитерском магазине продаются пирожные 4 сортов: наполеон, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных? Пирожные одного сорта считаются неразличимыми.
Решение. Зашифруем каждую покупку с помощью нулей и единиц. Напишем столько единиц, сколько куплено наполеонов, затем пишем 0, чтобы отделить пирожные одного типа от другого и т.д. Тогда каждой покупке будет соответствовать последовательность из семи единиц и трех нулей в различном порядке. Число всех таких покупок тогда будет равно числу перестановок с повторением:
.
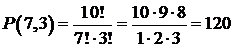
Заметим, что в рассматриваемой последовательности длины 10 из пирожных и разделителей нет никаких ограничений для расстановки разделителей (т.е. нулей). Они могут стоять в начале и в конце последовательности, любые два разделителя могут оказаться рядом. Действительно, здесь мы предполагаем, что покупка может быть абсолютно произвольной (пирожные могут оказаться только одного вида).
Таким образом, задача сводится к выбору трех позиций для разделителей из десяти возможных. Этот выбор можно сделать числом способов, равным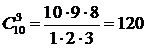 
. Получили тот же результат.
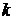
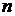
Определение 2: Группы, составленные из объектов, которые принадлежат одному из типов элементов, называют сочетаниями с повторениями.
Число всевозможных сочетаний с повторениями обозначают следующим символом: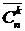 
.
Сочетания с повторениями, как было показано в примере, могут быть сведены к перестановкам с повторениями, поэтому имеем формулу:
.
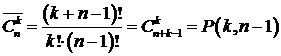
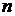
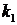
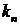
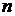
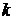
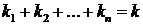
Доказательство. Пронумеруем элементы исходного множества числами от 1 до . Пусть в одно из сочетаний с повторениями вошло 
элементов под номером 1, 
элементов под номером 2, …, 
элементов под номером . Поскольку составляются группы из объектов, то 
.
Изобразим это сочетание с повторениями в виде последовательности из нулей и единиц. Единица будет обозначать каждый отдельный объект сочетания, нуль – разделитель между группами.
Поскольку сумма всех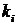 
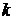
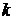
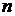
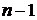
равна , то в построенной последовательности содержится единиц, а так как имеется различных по составу групп, то разделителей (нулей) будет 
. Верно обратное: каждой такой последовательности соответствует сочетание с определенными повторениями.
Таким образом, задача свелась к поиску ответа на вопрос: сколько различных последовательностей длины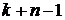 
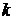
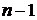
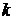
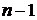
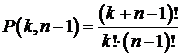
можно составить из единиц и нулей? Это есть число перестановок с повторениями из единиц и нулей:
.
А так как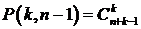 
, то формула доказана.
Пример 4. При принятии решения члены комитета голосуют: «за», «против», «воздержался». Сколько может быть возможных исходов голосования по данному решению?
Решение. Если нас интересует, кто и как голосовал, то тогда речь идет о размещениях с повторениями, что даст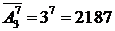 
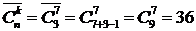
возможных исходов голосования. Если же не важно, кто и как голосовал, а только общий результат, то тогда речь идет о сочетаниях с повторениями. В этом случае имеем: 
возможных исходов голосования.
Замечание. Сочетания с повторениями и размещения с повторениями объединяет то, что нет никаких ограничений на число повторений элементов, кроме их общего числа в наборе. Поэтому в формулах 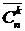и допустим случай, когда 
. Отличие сочетаний от размещений прежде всего в том, что сочетания – это неупорядоченный набор, а размещения – упорядоченный.
Источник
