- Основные формулы комбинаторики
- Как выбрать формулу комбинаторики?
- Перестановки
- Размещения
- Сочетания
- Комбинаторика
- Основное правило комбинаторики
- 1. Размещение (или упорядоченный выбор)
- 1.1 Число размещений с возвращением
- 1.2 Число размещений без возвращения
- 1.2 a. Перестановка из m различимых шаров
- 2. Сочетание (или неупорядоченный выбор)
- 2.1 Число сочетаний без возвращения
- 2.1.a. Перестановка из m шаров, неразличимых внутри групп
- 2.2 Число сочетаний с возвращением
- Литература
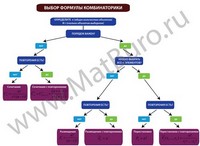
Основные формулы комбинаторики
Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.
Как выбрать формулу комбинаторики?
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:
- алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
- рекомендации по изучению комбинаторики,
- 6 задач с решениями и комментариями на каждую формулу.
Перестановки
Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно

Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов — уже 3628800 (больше 3 миллионов!).
Размещения
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $m$, а их число равно
Пример всех размещений из $n=3$ объектов (различных фигур) по $m=2$ — на картинке справа. Согласно формуле, их должно быть ровно $A_3^2=3\cdot (3-2+1)=3\cdot 2 =6$.
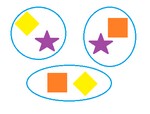
Сочетания
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $m$, а их число равно
Пример всех сочетаний из $n=3$ объектов (различных фигур) по $m=2$ — на картинке справа. Согласно формуле, их должно быть ровно $C_3^2=\frac<3!> <(3-2)!\cdot 2!>=3$. Ясно, что сочетаний всегда меньше чем размещений (так как при размещениях порядок важен, а для сочетаний — нет), причем именно в $m!$ раз, то есть верна формула связи:
Источник
Комбинаторика
Комбинаторика является одним из разделов математики, изучающая задачи расположения, сочетания, выбора объектов в различных ситуациях (условиях).
Иногда обсуждение «перестановок и сочетаний» начинается с вопроса, подобного следующему:
Сколькими способами может одеться человек, комбинируя три рубашки, два галстука и две пары ботинок?
Пусть первая координата указывает вариант выбора рубашки, вторая — галстука, а третья — ботинок.
(1,1,1) (1,1,2) (1,2,1) (1,2,2) для комбинации с первой рубашкой
(2,1,1) (2,1,2) (2,2,1) (2,2,2) для комбинации со второй рубашкой
(3,1,1) (3,1,2) (3,2,1) (3,2,2) для комбинации с третьей рубашкой
Эта совокупность является множеством всех упорядоченных пар.
Теперь понятно, что правильным ответом служит число 3 ∙ 2 ∙ 2 = 12.
Итак, сформулируем общее утверждение:
Основное правило комбинаторики
Пусть необходимо несколько раз произвести выбор. Существует m1 вариантов при первом выборе, m2 — при втором, m3 — при третьем и т.д.
Если каждый раз выбор производится без всяких ограничений, тогда общее число возможностей для всей последовательности выборов равно:
Теперь познакомимся с основными стандартными методами вычислений, используемыми при решении комбинаторных задач.
Рассуждения будем приводить на основе следующего примера:
Пусть урна содержит m различных шаров с номерами от 1 до m. Из неё извлекаются n шаров при соблюдении некоторых условий на способ извлечения. Для каждой модели вычисляются количества всех возможных исходов.
1. Размещение (или упорядоченный выбор)
1.1 Число размещений с возвращением
Шары извлекаются наудачу один за другим, причем каждый вынутый шар возвращается назад в урну прежде, чем будет извлечен следующий. При этом записываются номера шаров в порядке их появления.
Таким образом, мы имеем дело с упорядоченными наборами (a1. an), в которых каждое aj может принимать любое значение от 1 до m.
Основное правило сразу приводит к ответу m n для полного числа исходов.
1.2 Число размещений без возвращения
Шары извлекаются наудачу один за другим, однако в данной модели они не возвращаются обратно в урну. Мы снова имеем дело с упорядоченными наборами (a1. an), но уже с ограничением, что в них все aj различны. Конечно, должно выполняться неравенство n меньше или равно m. Основное правило напрямую не применимо. Тем не менее, принимая во внимание, что на каждом шаге число шаров в урне становится на один меньше, можем записать:
Данная модель имеет важный частный случай — модель перестановок.
1.2 a. Перестановка из m различимых шаров
Рассмотрим модель 1.2 при m = n.
Тогда все m шаров извлекаются один за другим без возвращений. Результатом выбора является набор из m занумерованных шаров, расставленных в некотором порядке. Полное количество возможностей совпадает с числом всех расположений элементов множества . Это число называется факториалом от m и обозначается
2. Сочетание (или неупорядоченный выбор)
Модель подразумевает, что порядок номеров вытянутых шаров не фиксируется. В отличие от модели размещений, наборы, отличающиеся только порядком следования элементов, считаются одинаковыми.
2.1 Число сочетаний без возвращения
Итак, вынутые шары не возвращаются назад в урну, а также не фиксируется порядок их номеров в процессе извлечения.
Другими словами, можно представить себе, что все n шаров вынимаются сразу за одно извлечение.
Следовательно, мы имеем дело с выбором произвольного подмножества размера n из множества размера m.
Из предыдущих рассуждений понятно, что упорядоченная выборка размера n порождает n! неупорядоченных, по каждой из которых можно однозначно восстановить исходную.
Из обсуждения модели 1.2 известно, что количество последовательных наборов размера n равно (m)n.
Обозначим за x искомое число исходов (подмножеств размера n). Проведенные выше рассуждения показывают, что
Отсюда получаем искомый ответ:
Если умножить числитель и знаменатель на (m-n)!, получим:

Выражение (*) называется биномиальным коэффициентом и играет важную роль в теории вероятностей.
Заметьте, что верно тождество
2.1.a. Перестановка из m шаров, неразличимых внутри групп
Допустим,что у нас есть m1 шаров цвета номер 1, m2 шаров цвета номер 2, . mr шаров цвета номер r. Цвета различаются, а шары одного цвета — нет.
Конечно, m1 + m2 +. + mr = m. Сколько существует отличающихся перестановок таких шаров?
Используя рассуждения из 1.2.a. для каждой первоначальной перестановки без различения шаров одного цвета в силу основного правила существует
новых способов размещения с учетом нумерации.
Рассуждения аналогичные проведенным для модели 2.1 показывают, что искомое число ненумерованных перестановок равно частному:
Число называется мультиномиальным (или полиномиальным) коэффициентов. Когда r=2, коэффициент сводится к биномиальному.
2.2 Число сочетаний с возвращением
Из урны извлекаются один за другим n шаров, каждый вынутый шар возвращается назад прежде, чем будет извлечен следующий.
При этом (возможно, повторяющиеся) номера всех вынутых шаров регистрируются в виде неупорядоченного набора (группы), т.е. без обращения внимания на порядок их появления.
Литература
К.Л. Чжун, Ф. АитСахлиа. Элементарный курс теории вероятностей. Стохастические процессы и финансовая математика. Перевод с английского М.Б. Лагутина, М.: БИНОМ. Лаборатория знаний, 2007
Источник
КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов ?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:

Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m (

Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.

Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:

Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
Источник