Количество способов размена монет

Задача о сумме

В знаменитой задаче с монетами, которыми необходимо отсчитать сдачу, как известно, есть две беды.
— первая – это количество номиналов монет,
— вторая – это количество разрядов числа, представляющего сдачу.
И обе эти величины оказывают экспоненциальное воздействие на нагрузку машины Тьюринга, которая собственно и занимается подсчётом.
Признавать, что человек имеет сразу две зависимости, не принято даже в обществе алкоголиков. Поэтому я решил подстраховаться и избавиться от одной из этих проблем заранее. Путь это будет количество номиналов монет.

В двух словах суть проблемы описывается так: экспоненциальная зависимость. То есть выпуск нового типа монет несуществующего доселе номинала влечёт за собой увеличение количества комбинаций монет в два раза. Ещё один номинал – ещё в два раза, и так до условной бесконечности. При галопирующей инфляции, когда новые монеты/купюры выпускаются достаточно часто, для решения задачи придётся покупать более мощный компьютер. А где на это взять деньги при галопирующей то инфляции?

Итак, решение, которое на самом деле достаточно просто.
Если представить отрезок от нуля до С (сдача) с нанесёнными на ней точками, соответствующими номиналам монет, то любой интеллектуальный человек увидит примерно следующую картинку: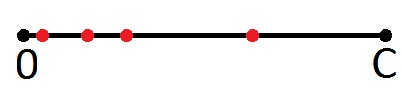

Ну, возможно в других цветах.
Итак, что мы можем сказать про красные точки? Конечно же то, что число, соответствующее любой этой точке, есть сумма, которую мы можем выдать в виде сдачи. Причём одной монетой. Возможно кто-то увидел что-то другое, но я, как художник, вкладывал именно этот смысл. И, как художник же, дорисую на этой картинке ещё одну точку, соответствующую сумме первой (слева направо) точки с этой же точкой (всё правильно: получится удвоенный номинал). Дорисую этим же цветом, ибо новая точка означает то же самое – эта сумма так же может быть сдачей.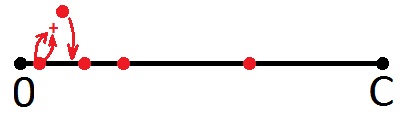

Далее беру первую точку и суммирую со второй, даже если вторая точка это предыдущая сумма (это неважно, ибо все точки здесь равны). Новую точку опять нанесу на отрезок.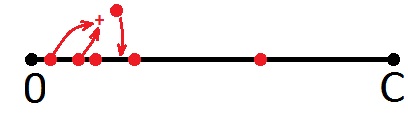

Если новая точка выходит за пределы отрезка, то ничего не рисуем, а возвращаемся к началу отрезка и берём следующую точку, то есть вторую. Далее то же самое (слева направо).
Собственно, когда точка С (напомню, это сдача) станет красной, можно считать, что решение найдено. А можно пройти полный цикл и найти оптимальное решение, что бы количество монет было минимальным.

С точки зрения программирования, здесь два цикла. Первый от 0 до С/2 (нет необходимости брать первую точку большей С/2, т.к. вторая точка всегда больше первой и в сумме они выйдут за границы отрезка). Второй цикл является встроенным в первый, он начинается с той же точки, на которую указывает внешний цикл и до момента, когда сумма покинет границы отрезка.
По сути это перебор: мы не теряем ни одного варианта, и гарантированно найдём оптимальное решение, или придём к выводу, что решения нет.

Давайте подсчитаем количество итерации внутри наших циклов. По внешнему циклу – это С/2, по внутреннему – где-то столько же. Умножим С/2 * С/2 = (С^2) / 4. Округлим до С в квадрате. Это наихудший вариант, когда весь наш отрезок просто состоит из красных точек. Если же между точками будут пробелы, количество итераций значительно уменьшится.
Как видим при определении сложности решения задачи мы не используем количество номиналов монет. Эта величина напрямую совсем никак не влияет на сложность решения. Влияют величины этих номиналов, скажем монета в 1 цент и сделает этот отрезок полностью красным. Поэтому эту монету лучше и не брать в расчёт, а в конце решения взять ближайшую к С красную точку и набросать сверху одноцентовиков. Но это уже момент оптимизации алгоритма, а она за рамками этой статьи.

Вот собственно и всё, что хотелось бы сказать. Рабочую версию программы можно найти здесь: github link

1. В файле init.h задать COINS_NUMBER — количество номиналов монет, и AMOUNT — сумма сдачи.
2. В файле coinc.c указать номиналы монет в массиве coins.
3. Под Linux запустить make_sh.
4. Запустить программу app на выполнение

Приведу какой-нибудь забавный пример. Представим, что в какой-нибудь стране к власти пришли математики и ввели в обращения 32 номинала монет: 2, 3, 5, 7, 11, 13, 17, 19… 131. Для удобства счёта выбрали только простые числа (ну не смешно ли?). И, что бы убедиться, что денежная реформа прошла успешно, послали в магазине гонца разменять купюру 5333 (тоже простое число). Кассир на стареньком одноядернике решил задачу: 39 монет номиналом 131 пифагороцентов, одну монету 127 и одну 97. Расчёт занял 3 секунды и чуть больше мегабайта памяти. Правительству доложили, что народ реформой доволен, считает быстро.

И пример, который чуточку сложнее проверить. Монеты, сто номиналов в такой вот странной последовательности: 0101, 0202, 0303… 9898, 9999, 100100. Сумма сдачи: 101010. Поиск решения занял 1 секунду и чуть больше мегабайта памяти. А решения, собственно, и нет, то есть нельзя такими монетами набрать такую сумму. С этими же монетами проверка суммы в 1 миллион займёт 26 мегабайт и сотни секунд, что говорит об экспоненциальной зависимости от суммы, но не количества номиналов монет.

Источник

Задача по информатике на собеседовании в IT-компанию. »Размен монет»

Всем привет! Сегодня решим задачу по информатике, которую часто дают на собеседованиях в различные IT-компании (или похожую ей).

Задача: Напишите программу, которая определит количество различных комбинаций американских монет(1 цент, 5 центов, 10 центов, 25 и 50 центов), которые могут сложиться в определенную сумму, введённую с клавиатуры. Максимальная сумма 1000 центов.

Решение: Рассмотрим на примере. Пусть сумма будет равна 25 центов.

Сначала пытаемся использовать самые большие монеты. Монета в 50 центов в данном случае не пригодится. Поэтому берём в 25 центов. Это уже 1 вариант. Так же мы можем разбить сумму в 25 центов и без монеты в 25 центов (Т.е использовав монеты достоинством в 10, 5, 1). На рисунке показан этот случай стрелкой влево.

Число 25 можно разбить, использовав 10-ти центовые монеты, а можно и более мелкими монетами(5, 1). Поэтом от 25-ти на рисунке идут опять две стрелочки. Если мы используем монету достоинством в 10 центов, то мы кладём 10 и нам теперь необходимо разбить уже 15. Число 15 опять мы может разбить, использовав 10-ти центовые монеты, а можно 15 разбить и более мелкими монетами. И т.д. Продолжая эту логику у нас от каждого числа будет по 2 стрелочки. Продолжаем раскладывать, пока у нас не получатся элементарные варианты. Количество вариантов обозначены красным цветом.

Почему от некоторых чисел на рисунке идёт по 1-му варианту ? Это происходит из-за того, что мы в этих вариантах решили разбить число самыми маленькими монетами в 1 цент. Таким образом, даже большие числа вроде 20, будут раскладываться в этих случаях единственным образом 20 = 1 + . + 1. А почему от 5 идёт два варианта ? Число пять можно разложить, как пяточком, так и по 1 центу.

Теперь просуммируем все числа красным цветом и получим количество вариантов. У нас получается число 13

Данный тип задач может попасться и на олимпиаде по информатике. Реализовывать будем на языке программирования C#!

Ещё одна схема для суммы 37 приведена на рисунке. Получается 24 комбинации.

Источник

Размен монет

Найдите количество различных способов разменять N рублей с помощью монет достоинством 1, 2, 5 и 10 рублей. Считайте, что есть неограниченное количество монет каждого типа.

Входные данные
Входная строка содержит одно натуральное число N – сумму, которую нужно разменять ( 1 ≤ N ≤ 10000 ).

Выходные данные
Программа должна вывести одно число: количество различных вариантов размена.

выходные данные
4

Задача на размен денег
Помогите пожалуйста Дано натуральное число n(n 5

Решение

Рассчитать номиналы монет, необходимых для покупки.
Во вселенной Гарри Поттера Министерство магии провело экономическую реформу. Старые галеоны, сикли.

Сколько надо монет для проверки типа автомата
В вашем офисе поставили 3 автомата, для напитков. Первый для кофе, второй для чая, а третий по.

Можно ли добавить в копилку ещё какое-то количество монет, не превышая ее вместимость?
Всем привет, помогите, пожалуйста, найти у меня ошибку. Задача звучит так: Реализуйте класс.

В массиве K(n) в порядке убывания представлены достоинства денежных знаков (купюр и монет)
В массиве K(n) в порядке убывания представлены достоинства денежных знаков (купюр и монет) валютной.

Монеты на какую сумму можно потратить, оставив по одному экземпляру каждого типа монет?
У Петра скопилась горка юбилейных монет, среди которых попадаются дубликаты. Монеты попадаются.

размен монет
сколькими способами можно разместить 10-копеечную монету монетами 1,2,3 и 5 копеек при условии, что.

Источник

Олимпиадное хобби. Размен монет

Привет. Сегодня понедельник, поэтому я решил, что стоит начать свой рабочий день с разогрева пальцев и мозга. Для тех кто не в курсе: мое олимпиадное хобби состоит в решении олимпиадных задач по программированию, которые я беру с сайта http://uva.onlinejudge.org/. Сегодня нам предстоит решить задачу о размене монет из области динамического программирования. Задача не очень сложная, но есть над чем поразмыслить, поэтому заинтересовавшихся прошу под кат. К слову, это третья наша задача, но, безусловно, из всех самая интересная.

Небольшое лирическое отступление.

Мой программистский путь начался далеко не в 3 года, когда многие будущие программисты уже разбирали калькулятор и делали из него компьютер. Я начал заниматься программированием в школе в 8 классе. К слову сказать, моя школа была далека от технического направления, поэтому в своих начинаниях я был почти одинок. Но, благодаря директору нашей школы, у нас был «кружок» по программированию, где мы готовились к школьной олимпиаде по программированию. Нас там было не более трех человек единовременно, но нашего преподавателя, к счастью, это не расстраивало. Моим преподавателем программирования был Кавокин А.А., отчасти благодаря ему я и встал на столь удивительный путь программиста. Так вот, каждый урок наш наставник начинал с логической задачки, чтобы мы расшевелили свои извилины. Это мне настолько нравилось в школе, что я решил вас тоже так помучить, поэтому сегодня мы начнем с небольшой логической задачки, которая поможет нам размяться.

Логическая задачка для разминки:

В нашем городе проезд в общественном транспорте оплачивается непосредственно во время поездки, для чего по автобусу курсирует кондуктор, собирая со всех плату за проезд. Стоимость билета составляет 20 рублей. Однажды, на одной из остановок в автобус зашли 5 человек. Один из них молча заплатил кондуктору 100 рублей, и тот, не задавая никаких вопросов, отсчитал 5 билетов и отдал платившему. Вопрос: как кондуктор догадался, что оплата происходит сразу за всех пятерых, при условии, что ничто не указывало на то, что все они были вместе?

Позволю оставить задачу без ответа, потому что уверен в вашей сообразительности. А как только в комментариях появится правильный ответ, сразу вынесу ссылку сюда.
UPD: Ответ найден в комментарии пользователя ogra

Условие

Надеюсь задачка, которую я вам подкинул для разогрева, успешно подействует на вашу мозговую активность. Сейчас мы, наконец-то займемся решением олимпиадной задачи. Наша сегодняшняя задача — это задача о размене монет.

Краткий перевод условия задачи

После закупки в большом универмаге Мелу досталась сдача в размере 17 центов. Он получил одну десятицентовую монету, одну пятицентовую и 2 монеты по 1 центу. Позже, в этот же день, он делал покупки в мини-маркете, где тоже получил сдачу в размере 17 центов. На этот раз он получил две монеты по 5 центов и 7 монет по 1 центу. Тогда Мел задался вопросом: «Как много магазинов я могу посетить и получить сдачу в 17 центов различным набором монет?» После небольшого мозгового штурма, он определил, что ответ 6. Тогда он бросил вызов вам для решения более общего случая.

Напишите программу, которая определит количество различных комбинаций американских монет(1 цент, 5 центов, 10 центов, 25 и 50 центов), которые могут сложиться в определенную сумму.

Входные данные: ввод будет состоять из множества чисел между 0 и 30000 включительно, по одному в каждой строке.

Выходные данные: на каждое входное число, нужно определить число комбинаций и вывести, как показано в примере.

Output:
There are 6 ways to produce 17 cents change.
There are 4 ways to produce 11 cents change.
There is only 1 way to produce 4 cents change.

Как обычно, рекомендую вам самим попытаться решить задачу. А как только решите, возвращайтесь к нам и хвастайтесь своим результатом.

Решение

Задача явно из области динамического программирования, а такие задачи, как правило, решаются с помощью рекурсивных зависимостей. Нам необходимо определить, какая именно рекурсивная зависимость в нашем случае.

Можно сразу заметить, что число комбинаций не отличается при сдаче от 1 цента до 4 — это 1 вариант, при сдаче от 5 центов до 9 — это 2 варианта, при сдаче от 10 центов до 14 — это 4 варианта и т.д. Это происходит потому, что внутри такой «пятерки» монеты достоинством в 1 цент невозможно ничем заменить. Таким образом мы определили, что решать задачу для каждого числа бессмысленно, поэтому мы будем решать ее для каждой «пятерки».

Также можно заметить, комбинации для каждой следующей «пятерки» точно повторяют комбинации предыдущей «пятерки» (с добавлением в конец комбинации нужного числа монет по 1 центу) и некоторого числа новых комбинаций. Становится понятным, что число комбинаций следующей «пятерки» имеет зависимость от числа комбинаций предыдущих «пятерок». Нарисуем таблицу, где столбцами будут «пятерки», а строками виды монет, а на пресечении будет определяться, какое количество новых комбинаций породил данных вид монет ( в комбинации со всеми более мелкими) на конкретном шаге — «пятерке»:

1	5	10	15	20	25	30	35	40	45	50	55
1	1	0	0	0	0	0	0	0	0	0	0	0
5	0	1	1	1	1	1	1	1	1	1	1	1
10	0	0	1	1	2	2	3	3	4	4	5	5
25	0	0	0	0	0	1	1	2	2	3	4	5
50	0	0	0	0	0	0	0	0	0	0	1	1
∑	1	2	4	6	9	13	18	24	31	39	50	62

В последней строке выведено число комбинаций на данной «пятерке»
К примеру: на шаге 35 (8 пятерка: 35-39)
имея только 1 центовую монету, новых комбинаций не появляется,
из монет 1 цент и 5 центов, можно выдумать 1 новую комбинацию: 5+5+5+5+5+5+5+1(от 0 до 4)
1 цент, 5 центов, 10 центов — 3 комбинации: 10+10+10+5+1(от 0 до 4), 10+10+5+5+5+1, 10+5*5+1
1, 5, 10, 25 — 2 новых комбинации: 25+10+1, 25+5+5+1

Число новых комбинаций на каждом шаге из монет 1 цент и 5 центов равняется 1, потому что это комбинация порождается добавлением 5 центовой монеты к предыдущей комбинации. Т.е. для второй пятерки 5+1, потом 5+5+1, потом 5+5+5+1 и т.д., по 1 новой комбинации на каждом шаге.
Также в этой таблице не трудно углядеть рекурсивную зависимость: число новых комбинаций на шаге i, составленных из монет 1-10 равняется числу новых комбинаций из монет 1-5 на шаге i-1 плюс число новых комбинаций из монет 1-10 на шаге i-2 (когда у нас в распоряжении было на 1 десятицентовую монету меньше). Аналогично для 25-ти центовой монеты и 50-ти центовой монеты.

В итоге мы имеем 2 формулы и 3 рекурсивных зависимости:
N(1, i) = 0, кроме N(1, 0) = 1
N(5, i) = 1
N(10, i) = N(5, i-1) + N(10, i-2)
N(25, i) = N(10, i-3) + N(25, i-5)
N(50, i) = N(25, i-5) + N(50, i-10)
S(i) = S(i-1) + N(1, i) + N(5, i) + N(10, i) + N(25, i) + N(50, i)
Где N — это матрица, определенная выше, а S — искомое число комбинаций.

Теперь нам остается лишь просчитать нужное число шагов от начала до запрашиваемой «пятерки», подсчитывая на каждом шаге общее число комбинаций (S). Учитывая тот факт, что тестов в задаче будет много, можно использовать для новых тестов, ранее просчитанный кусок матрицы и дополнять лишь ее недостающую часть. Еще очень важно понимать, что при максимальной сумме, заданной условием задачи: 30000 центов, суммарное число комбинаций перевалит за пределы int и даже long, поэтому для подсчета числа комбинаций рекомендую использовать 8 байтовые беззнаковые переменные.

Полагаю, что есть более изящное решение, чем предложенное выше, но я его пока не вижу, поэтому жду от вас интересных алгоритмов. Мое решение на C++ можно скачать тут. Проверить правильность своего решения можно здесь (требуется регистрация). Удачи, господа!

Источник