Количество способов дать сдачу

Определить число способов выдачи сдачи в сумме n рублей

В торговом автомате сдача выдается монетами в 1, 2, 5 и 10 руб. Написать программу, которая определит число способов выдачи сдачи в сумме nрублей ( n Помощь в написании контрольных, курсовых и дипломных работ здесь

Программа выдачи сдачи в N рублей для автомата, который имеет в распоряжении только монеты в 2 и 5 рублей
Ребятки, спасайте. На языке низкого уровня написать программу выдачи сдачи в N рублей для.

Вложенные циклы. Определить число способов выплаты суммы n рублей
ЗАДАЧА НА ТЕМУ ВЛОЖЕННЫЕ ЦИКЛЫ Дано натуральное число n(n 1

Требуется определить количество способов выплаты n рублей монетами по 1, 2, 5 и 10 рублей
Формат входных данных На вход программе дается одно натуральное число n (n ≤ 99). Формат.

Требуется определить количество способов выплаты n рублей монетами по 1, 2, 5 и 10 рублей
Требуется определить количество способов выплаты nn рублей монетами по 1, 2, 5 и 10 рублей. На.

Определение сдачи с 50 рублей покупателю, совершившему покупку стоимостью менее 50 рублей
Составьте алгоритм и напишите программу, которая определяет сдачу с 50 рублей, возвращаемую.

Найти минимальное количество монет для выдачи сдачи
Пожалуйста, помогите найти ошибку! Программа ищет минимальное кол-во монет, для выдачи сдачи. У.

Найти количество возможных способов выдачи зарплаты
В задаче нужно найти колличество возможных способов выдачи зарплаты 1$ 2$ 5$ и 10$ купюрами.

Определить число возможных способов подъема по лестнице
Лестница По пути в школу Анна должна подниматься по лестнице из n ступенек. Одним своим шагом она.

Источник

Задача о сумме

В знаменитой задаче с монетами, которыми необходимо отсчитать сдачу, как известно, есть две беды.
— первая – это количество номиналов монет,
— вторая – это количество разрядов числа, представляющего сдачу.
И обе эти величины оказывают экспоненциальное воздействие на нагрузку машины Тьюринга, которая собственно и занимается подсчётом.
Признавать, что человек имеет сразу две зависимости, не принято даже в обществе алкоголиков. Поэтому я решил подстраховаться и избавиться от одной из этих проблем заранее. Путь это будет количество номиналов монет.

В двух словах суть проблемы описывается так: экспоненциальная зависимость. То есть выпуск нового типа монет несуществующего доселе номинала влечёт за собой увеличение количества комбинаций монет в два раза. Ещё один номинал – ещё в два раза, и так до условной бесконечности. При галопирующей инфляции, когда новые монеты/купюры выпускаются достаточно часто, для решения задачи придётся покупать более мощный компьютер. А где на это взять деньги при галопирующей то инфляции?

Итак, решение, которое на самом деле достаточно просто.
Если представить отрезок от нуля до С (сдача) с нанесёнными на ней точками, соответствующими номиналам монет, то любой интеллектуальный человек увидит примерно следующую картинку: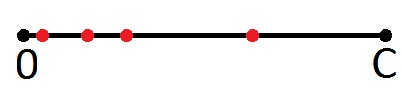

Ну, возможно в других цветах.
Итак, что мы можем сказать про красные точки? Конечно же то, что число, соответствующее любой этой точке, есть сумма, которую мы можем выдать в виде сдачи. Причём одной монетой. Возможно кто-то увидел что-то другое, но я, как художник, вкладывал именно этот смысл. И, как художник же, дорисую на этой картинке ещё одну точку, соответствующую сумме первой (слева направо) точки с этой же точкой (всё правильно: получится удвоенный номинал). Дорисую этим же цветом, ибо новая точка означает то же самое – эта сумма так же может быть сдачей.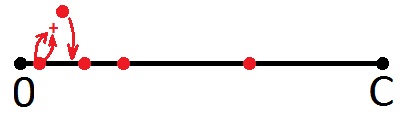

Далее беру первую точку и суммирую со второй, даже если вторая точка это предыдущая сумма (это неважно, ибо все точки здесь равны). Новую точку опять нанесу на отрезок.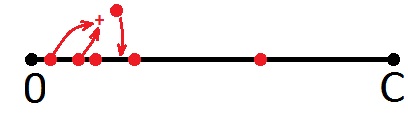

Если новая точка выходит за пределы отрезка, то ничего не рисуем, а возвращаемся к началу отрезка и берём следующую точку, то есть вторую. Далее то же самое (слева направо).
Собственно, когда точка С (напомню, это сдача) станет красной, можно считать, что решение найдено. А можно пройти полный цикл и найти оптимальное решение, что бы количество монет было минимальным.

С точки зрения программирования, здесь два цикла. Первый от 0 до С/2 (нет необходимости брать первую точку большей С/2, т.к. вторая точка всегда больше первой и в сумме они выйдут за границы отрезка). Второй цикл является встроенным в первый, он начинается с той же точки, на которую указывает внешний цикл и до момента, когда сумма покинет границы отрезка.
По сути это перебор: мы не теряем ни одного варианта, и гарантированно найдём оптимальное решение, или придём к выводу, что решения нет.

Давайте подсчитаем количество итерации внутри наших циклов. По внешнему циклу – это С/2, по внутреннему – где-то столько же. Умножим С/2 * С/2 = (С^2) / 4. Округлим до С в квадрате. Это наихудший вариант, когда весь наш отрезок просто состоит из красных точек. Если же между точками будут пробелы, количество итераций значительно уменьшится.
Как видим при определении сложности решения задачи мы не используем количество номиналов монет. Эта величина напрямую совсем никак не влияет на сложность решения. Влияют величины этих номиналов, скажем монета в 1 цент и сделает этот отрезок полностью красным. Поэтому эту монету лучше и не брать в расчёт, а в конце решения взять ближайшую к С красную точку и набросать сверху одноцентовиков. Но это уже момент оптимизации алгоритма, а она за рамками этой статьи.

Вот собственно и всё, что хотелось бы сказать. Рабочую версию программы можно найти здесь: github link

1. В файле init.h задать COINS_NUMBER — количество номиналов монет, и AMOUNT — сумма сдачи.
2. В файле coinc.c указать номиналы монет в массиве coins.
3. Под Linux запустить make_sh.
4. Запустить программу app на выполнение

Приведу какой-нибудь забавный пример. Представим, что в какой-нибудь стране к власти пришли математики и ввели в обращения 32 номинала монет: 2, 3, 5, 7, 11, 13, 17, 19… 131. Для удобства счёта выбрали только простые числа (ну не смешно ли?). И, что бы убедиться, что денежная реформа прошла успешно, послали в магазине гонца разменять купюру 5333 (тоже простое число). Кассир на стареньком одноядернике решил задачу: 39 монет номиналом 131 пифагороцентов, одну монету 127 и одну 97. Расчёт занял 3 секунды и чуть больше мегабайта памяти. Правительству доложили, что народ реформой доволен, считает быстро.

И пример, который чуточку сложнее проверить. Монеты, сто номиналов в такой вот странной последовательности: 0101, 0202, 0303… 9898, 9999, 100100. Сумма сдачи: 101010. Поиск решения занял 1 секунду и чуть больше мегабайта памяти. А решения, собственно, и нет, то есть нельзя такими монетами набрать такую сумму. С этими же монетами проверка суммы в 1 миллион займёт 26 мегабайт и сотни секунд, что говорит об экспоненциальной зависимости от суммы, но не количества номиналов монет.

Источник

Написать функцию, считающую количество способов отдать сдачу величины sum

Надо написать функцию, считающую количество способов отдать сдачу величины sum используя монеты достоинством ai,
все ai различны.
Например :
Сдача размера 10 монетками <5,2,1>
10=5+5
10=5+2+2+1
.
Достоинства передовать в векторе.

Можно пример кода, пж-та?

Написать программу, считающую количество цифр в строке
Написать программу, считающую количество цифр в строке.

Написать программу считающую количество строк в строке
Написать программу считающую количество строк в строке

Написать программу, считающую количество русских букв в строке
Программа должна считать количество букв кириллицы в строке, но почему-то выводит 0. #include.

написать программу считающую количество гласных букв в едите
написать программу считающую количество гласных букв в едите

По русски, то что было написано а C++

Если money — сумма для размена монетами coin = , где
c_1 1

Написать функцию sum с переменным числом параметров, которая находит вещественную сумму
Написать функцию sum с переменным числом параметров, которая находит вещественную сумму заданных.

Написать функцию sum с переменным числом параметров, которая находит сумму чисел типа int
Написать функцию sum с переменным числом параметров, которая находит сумму чисел типа int. Написать.

Разработать рекурсивную функцию, определяющую количество способов продвижения шашки на n-ю клетку.
Имеется полоска клетчатой бумаги шириной в одну клетку и длиной в n клеток. На первой клетке.

Написать функцию SUM (int M, int N) / С++ для начинающих
Написать функцию SUM (int M, int N), которая вычисляет и возвращает сумму всех чисел кратных 3 и 9.

Источник

Зона кода

Рассмотрим следующую задачу.

Каким количеством способов можно разменять тысячерублёвую купюру монетами по 1руб., 2руб., 5руб., 10руб.?

Решим задачу четырьмя способами. Различаться они будут степенью использования в них математического аппарата. В первом способе математика использоваться почти не будет: мы сразу же напишем программу. А в последнем нам удастся обойтись без программирования вообще: задача будет решена математически. Второй и третий способы будут занимать промежуточное положение между первым и последним. Все способы в порядке возрастания степени участия в них математики мы весьма условно назовём способами «двоечника», «троечника», «хорошиста» и «отличника».

Интересно будет проследить за тем, как, по мере перехода от «двоечника» к «троечнику» и от «троечника» к «хорошисту», объёмы предварительных математических выкладок будут расти, а программы будут становиться всё более и более эффективными.

Надеюсь, что словосочетания «математический аппарат» и «математические выкладки» не отпугнут читателя от ознакомления со статьёй. Математику мы будем использовать достаточно простую, да и программы будут простыми тоже, поэтому данный материал можно смело рекомендовать для прочтения новичкам.

Способ «двоечника»

Первое же, что может прийти на ум – это метод перебора. Ясно, что в любом размене тысячерублёвой купюры десятирублёвых монет может быть от 0 до 100, пятирублёвых – от 0 до 200, двухрублёвых – от 0 до 500 и рублёвых – от 0 до 1000. Переберём всевозможные наборы из перечисленных монет, в которых монета каждого достоинства встречается число раз, попадающее в соответствующий ей диапазон. Для каждого такого набора вычислим его рублёвый эквивалент и подсчитаем случаи, в которых он будет равен 1000р.

Программу, реализующую такой ломовой перебор, написать очень легко:

Думаю, программа проста для понимания. Переменная s – это счётчик случаев, в которых количество рублей в наборе равно 1000. Во внешнем цикле перебираем всевозможные количества «десяток», во вложенном в него – количества «пятёрок», далее – количества «двушек», наконец, в самом внутреннем цикле перебираются количества рублей.

Итак, мы имеем 4 вложенных друг в друга цикла, общее количество итераций самого внутреннего цикла – более 10,1 млрд. На моём среднем по мощности ноутбуке программа работает полминуты! Но, несмотря на свою чудовищную неэффективность, она выдаёт правильный ответ – 1712051. Задача решена!

Если мы разделим ответ на количество всех итераций и выразим частное в процентах, то получим примерно 0,017%. Этот процент можно считать «коэффициентом полезного действия» данного метода. Именно такова доля «полезных» итераций в их общем количестве. Таким образом, примерно 99,98% итераций – это условный «балласт», на который тратится компьютерное время. Давайте избавимся от этих трат.

Способ «троечника»

Изменим программу. Внешний цикл оставим нетронутым. Во вложенном в него цикле изменим верхний предел изменения переменной b . Новый предел, который мы будем хранить в переменной m , теперь будет зависеть от текущего значения переменной a . Понятно, что для любого значения a значение b должно быть таково, чтобы выполнялось неравенство 10 * a + 5 * b . Это означает, что значение m , т. е. максимально возможное значение b , должно удовлетворять равенству 10 * a + 5 * m = 1000 , откуда m = 200 — 2 * a .

Что касается третьего и четвёртого цикла, то они нам не нужны. Действительно, если фиксировано количество «десяток» ( a ) и «пятёрок» ( b ), то совсем несложно подсчитать, каким количеством способов можно представить оставшуюся сумму (т. е. 1000 — 10 * a — 5 * b ) в виде «двушек» и рублей.

Это число способов равно максимальному количеству «двушек», которое может «поместиться» в оставшейся сумме (обозначим его, например, p ), сложенному с единицей. Объясняется это тем, что любое количество двухрублёвых монет от 1 до p может быть дополнено рублёвыми монетами до оставшейся суммы, а добавляемая к p единица соответствует единственному способу представления оставшейся суммы без использования «двушек».

Для получения p нужно выполнить целочисленное деление оставшейся суммы на 2. Таким образом, количество способов представления оставшейся суммы в виде двухрублёвых и однорублёвых монет (т. е. p + 1 ) равно (1000 — 10 * a — 5 * b) / 2 + 1 (деление на 2 здесь, разумеется, целочисленное). Именно это количество мы на каждой итерации внутреннего цикла будем теперь добавлять к счётчику s .

Этих выкладок уже вполне достаточно, чтобы написать второй вариант программы:

Программа выдаёт тот же результат, что и раньше, а время её работы составляет доли секунды. Это программа уже построена на подсчёте искомого количества способов, а не на переборе огромного количества вариантов, среди которых имеется львиная доля тех, которые нас не устраивают.

Несложно подсчитать общее число итераций внутреннего цикла:

∑ a = 0 100 200 — 2 a + 1 = ∑ a = 0 100 201 — 2 ∑ a = 0 100 a = 201 · 101 — 2 · 100 · 101 2 = 101 2 = 10201 .

Здесь мы использовали хорошо известные формулы для нахождения сумм:

∑ k = 0 n c = n + 1 c , ∑ k = 0 n k = n n + 1 2 .

Как мы видим, общее число итераций внутреннего цикла, по сравнению с предыдущим вариантом, снизилось на 6 порядков!

Заметим, что если бы мы решали задачу, в которой размен тысячи необходимо было осуществлять с помощью монет достоинством 1руб., 5руб., 10руб., то на каждой внутренней итерации нужно было бы увеличивать счётчик на 1. Это означает, что окончательное его значение совпало бы с общим числом внутренних итераций, т. е. с числом 10201. Таким, образом, мы, в качестве побочного эффекта, получили аналитическое решение задачи о количестве способов, которым можно осуществить описанный в начале абзаца обмен. Это число равно 10201.

Дальнейшие усовершенствования программы уже не приведут к хоть сколько-нибудь заметному увеличению производительности, поскольку программа уже выполняется почти мгновенно. Однако, из любви к искусству программирования, останавливаться мы не будем.

Способ «хорошиста»

В этом разделе мы получим выражение искомого количества способов размена в виде суммы, поле чего напишем программу для её вычисления.

Каждому способу размена тысячерублёвой купюры, удовлетворяющему условию нашей задачи, можно поставить в соответствие число t – суммарный рублёвый эквивалент всех однорублёвых и двухрублёвых монет, использующихся при размене данным способом. Для каждого t создадим группу, содержащую все способы размена, соответствующие t. Таким образом, каждой группе способов будет соответствовать своё t.

Несложно заметить, что t может принимать значения 0, 5, 10, . 1000. Таким образом, количество групп равно 201. Пусть s_k – число способов размена, содержащихся в группе, соответствующей значению t, равному 5k. Тогда S – искомое количество способов размена тысячерублёвой купюры, можно представить в виде:

S = ∑ k = 0 200 s k .

Выразим s_k через k. Для этого представим s_k в виде u_kv_k, где u_k – число способов, которыми можно набрать 5k рублей однорублёвыми и двухрублёвыми монетами, а v_k – число способов, которыми можно набрать оставшиеся 1000-5k рублей пятирублёвыми и десятирублёвыми монетами.

Найдём u_k. Воспользуемся способом, уже применявшимся нами в предыдущем разделе: разделим 5k на 2 «нацело» и добавим единицу:

Квадратные скобки здесь обозначают целую часть заключённого в них числа.

Теперь найдём v_k. Задача о нахождении количества способов набора 1000-5k рублей пятирублёвыми и десятирублёвыми монетами эквивалентна задачи о нахождении количества способов набора однорублёвыми и двухрублёвыми монетами суммы в 5 раз меньшей, т. е. 200-k рублей. Снова делим на 2 «нацело» и добавляем единицу:

v k = 200 — k 2 + 1 = 100 — k 2 + 1 = 101 — k 2 .

В итоге, получаем:

s k = u k · v k = 5 k 2 + 1 · 101 — k 2 ,

S = ∑ k = 0 200 5 k 2 + 1 · 101 — k 2 .

Формула получена, теперь можно составлять программу:

Заметим, что при написании программы выражение 101 — k 2 было закодировано как (202 — k) / 2 .

Программа выдаёт всё тот же результат – 1712051, используя при этом один-единственный цикл, в ходе которого выполняется 201 итерация.

Способ «отличника»

А теперь давайте решим задачу без использования программирования. Частью нашего решения являются математические выкладки, уже выполненные в предыдущем разделе. Нам остаётся лишь найти число S, воспользовавшись последней формулой предыдущего раздела.

Индекс k, принимающий все целые чётные значения от 0 до 200 включительно, можно представить в виде 2m, где новый индекс m принимает все целые значения от 0 до 100 включительно. Воспользовавшись заменой k=2m, запишем S₀ в виде суммы и найдём её:

S 0 = ∑ m = 0 100 5 · 2 m 2 + 1 · 101 — 2 m 2 = ∑ m = 0 100 5 m + 1 · 101 — m =
= ∑ m = 0 100 — 5 m 2 + 504 m + 101 = — 5 ∑ m = 0 100 m 2 + 504 ∑ m = 0 100 m + ∑ m = 0 100 101 = — 5 · 100 · 101 · 201 6 +
+ 504 · 100 · 101 2 + 101 2 = — 1691750 + 2545200 + 10201 = 863651 .

Здесь мы использовали три формулы, позволяющие вычислять суммы. Две из них мы приводили ранее, а третью приведём сейчас:

∑ k = 0 n k 2 = n n + 1 2 n + 1 6 .

Эти же три формулы понадобятся нам и для нахождения S₁.

Индекс k, принимающий все целые нечётные значения от 1 до 199 включительно, можно представить в виде 2m+1, где новый индекс m принимает все целые значения от 0 до 99 включительно. Воспользовавшись заменой k=2m+1, запишем S₁ в виде суммы и найдём её:

S 1 = ∑ m = 0 99 5 · 2 m + 1 2 + 1 · 101 — 2 m + 1 2 = ∑ m = 0 99 5 m + 3 + 1 2 · 100 + 1 2 — m =
= ∑ m = 0 99 5 m + 3 · 100 — m = ∑ m = 0 99 — 5 m 2 + 497 m + 300 = — 5 ∑ m = 0 99 m 2 + 497 ∑ m = 0 99 m + ∑ m = 0 99 300 =
= — 5 · 99 · 100 · 199 6 + 497 · 99 · 100 2 + 100 · 300 = — 1641750 + 2460150 + 30000 = 848400 .

S = S 1 + S 2 = 863651 + 848400 = 1712051 .

Выводы

Итак, мы решили задачу 4-мя способами. Первые 3 из них включали в себя написание программ. Для каждой из них было указано число итераций внутреннего цикла. Данная информация позволяет приближённо сравнить программы по производительности. Однако сравнение будет более точным, если в нём будут участвовать количества операций умножения и деления, задействованных в программах. Известно, что эти 2 операции требуют для своего выполнения значительно большего количества процессорного времени, чем операции сложения и вычитания, поэтому последними двумя мы пренебрежём.

Соберём в таблицу информацию о количествах циклов, итераций внутреннего цикла и числе операций умножения и деления.

Программа	Количество циклов	Количество итераций внутреннего цикла	Количество операций умножения и деления
«двоечника»	4	10 180 971 801	30 542 915 403
«троечника»	2	10 201	30 704
«хорошиста»	1	201	804

Как мы видим, информация, приведённая в последнем столбце, не вносит существенных корректив в результаты сравнений производительности программ. В соответствии с ней, вторая программа превосходит по производительности первую почти в 10 6 раз, а третья вторую – почти в 40 раз. В первом случае разрыв гигантский, а во втором – небольшой. «На глаз» заметить разницу во временах выполнения второй и третьей программ невозможно.

В заключение статьи проведём забавный мысленный эксперимент. Представим, что 4-м человекам предоставили в распоряжение компьютеры, бумагу, ручки и предложили решить нашу задачу. Предположим, что каждый из них выбрал один из способов, приведённых в статье, причём все выбрали разные способы. Будем считать, что способности этих людей примерно равны, тем не менее, назовём их условно «двоечником», «троечником», «хорошистом» и «отличником» в соответствии с выбранными ими способами. Зададимся вопросом: кто из них быстрее всех справится с задачей, а кто – медленнее?

Как мне представляется, «двоечник» решит задачу достаточно быстро. Например, за минуту придумает алгоритм, за минуту его реализует на компьютере, через полминуты работы программы ответ будет готов. «Троечник» будет возиться с алгоритмом на несколько минут дольше «двоечника», и, хоть его программа выполнится за доли секунды, по общему количеству времени «двоечнику» он уступит.

«Хорошисту» придётся разрабатывать алгоритм ещё дольше, и «троечнику» он проиграет. А вот отличник может в своих выкладках вообще увязнуть и потратить на решение полчаса или даже больше. Таким образом, он, скорее всего, «с треском» проиграет всем остальным.

Результаты могут показаться парадоксальными: интеллект проигрывает грубой ломовой силе. Означает ли это, что особого смысла в оптимизации программ может и не быть?

Вопрос очень простой, и я думаю, что ответ читателю известен. Если программа используется однократно, то, действительно, нет особой разницы в том, работает она полминуты или тысячную долю секунды. Но такие программы – редкость. В подавляющем большинстве случаев программное обеспечение рассчитано на многократное применение. И если на одном компьютере программа запускается на выполнение пару сотен тысяч раз, то снижение времени её работы даже на полсекунды весьма существенно! Ведь в данном примере суммарный выигрыш по времени превысит сутки! В таких случаях уместность оптимизации очевидна.

Источник