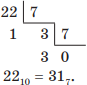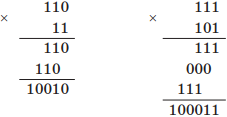Количество информации способы представления информации

Виды информации. Представление информации.

По способу восприятия информации человеком можно выделить визуальную (зрительную), аудиальную (звуковую), обонятельную (запахи) вкусовую, тактильную (осязательную), вестибулярную и мышечную информацию (рис.3).

Визуальную информацию люди воспринимают с помощью глаз. Человек может увидеть объект или явление, букву или цифру, картину или фильм, схему или карту, жест или танец. Аудиальную информацию люди воспринимают с помощью ушей. Человек может услышать произвольные звуки, шум, музыку, пение и речь. Обонятельную информацию, или запахи, человек воспринимает с помощью носа. Запах можно охарактеризовать как терпкий или пряный, приятный или неприятный, тяжелый или легкий. Вкусовую информацию человек воспринимает с помощью языка. Вкус может быть горький или сладкий, кислый или соленый. Тактильную информацию человек воспринимает кожей. Прикасаясь к предмету, можно определить его температуру (холодный или горячий) и вид поверхности (гладкая или шероховатая, мокрая или сухая). Вестибулярную информацию человек воспринимает с помощью вестибулярного аппарата, который отслеживает положение тела человека в трехмерном пространстве. Летя в самолете и не видя горизонта, человек может определить, куда и как он перемещается: вверх или вниз, вправо или влево, ускоренно или замедленно. Мышечную информацию люди воспринимают с помощью мышц. Закрыв глаза, человек не пронесет ложку с супом мимо своего рта, может дотронуться указательным пальцем до своего носа, сравнить массу гирь, одинаковых на ощупь.

Воспринимать информацию могут не только люди, но и животные, и растения. Однако в отличие от людей, восприятие информации животными и растениями имеет свои особенности. Например, слоны способны воспринимать звуки, которые не слышит человек, у собак лучше всего развито обоняние, у летучих мышей – слух, а растения могут получать информацию с помощью корней и листьев. Несмотря на эти особенности, в живой природе, так же как и в мире людей, информация играет важную роль в обеспечении жизненных процессов. Воспринимаемую с помощью органов чувств информацию человек стремится выразить так, чтобы она была понятна другим. Одну и ту же информацию, в зависимости от цели деятельности, можно выразить разными способами и представить в разной форме.

По форме представления принято выделять числовую, текстовую, графическую, звуковую и комбинированную информацию (рис. 4).

Рис. 4. Виды информации по форме представления

Например, если человек хочет выучить слова песни наизусть, то, скорее всего, он запишет стихи с помощью букв. В этом случае информация будет представлена в текстовой форме. Запомнить мелодию песни позволит прослушивание этой песни в исполнении певца или музыканта. В этом случае информация будет представлена в звуковой форме. Образ, навеянный стихами или мелодией, можно изобразить в графической форме с помощью рисунка.

Для того чтобы выяснить количество поклонников исполнителя песни, необходимо их подсчитать и результат представить в числовой форме. Каждая из этих форм представления информации имеет свои особенности. Графическая информация наиболее доступна, так как срезу передает визуальный образ.

С помощью текстовой и звуковой информации можно представить исчерпывающие разъяснения. Числовая информация дает возможность проводить различные сравнения и вычисления. Поэтому чаще всего информацию представляют в комбинированной форме. Частным случаем комбинированной информации является мультимедийная информация , когда текстовая и числовая информация сочетается со звуковой и графической информацией, с видеоизображением .

Для представления информации человек использует различные знаки. Один и тот же знак может иметь разный смысл. Если человек наделил знак смыслом, то этот знак называют символом

Например, нарисованный овал может означать или букву «О», или цифру ноль, или химический элемент кислород, или геометрическую фигуру. В нашем примере нарисованный овал – это знак. Буква, цифра и обозначение химического элемента являются символами.

Для того чтобы понимать смысл информации, представленной с помощью символов, человеку необходимо знать не только символы, но и правила составления сообщений из этих символов. Говоря другими словами, человеку необходимо знать язык. Язык может быть разговорным, языком рисунков, мимики и жестов, языком науки и искусства.

Выделяют естественные (разговорные) и искусственные языки (рис. 5).

Естественные языки исторически сложились в процессе развития человеческой цивилизации. К естественным языкам относятся русский, английский, китайский и многие другие языки. В мире насчитывается более 10 тыс. разных языков, диалектов и наречий.

Искусственные языки специально созданы для профессионального применения в какой-либо области человеческой деятельности. Некоторые искусственные языки складывались в течение длительного исторического периода, например язык математических обозначений. С этой точки зрения они мало отличаются от естественных языков. Примерами искусственных языков являются эсперанто, языки программирования, язык математики, язык химии, язык логики, язык флажков на флоте, язык дорожных знаков.

Некоторые естественные языки имеют искусственно созданные алфавиты. Так, например, авторами русского языка являются Кирилл и Мефодий.

Представление информации с помощью определенного языка всегда связано с алфавитом. Алфавит содержит конечный набор символов, из которых можно составить как угодно много слов. Все символы в алфавите упорядочены.

Количество символов в алфавите называют мощность алфавита.

Представленную информацию можно преобразовать из одной последовательности знаков в другую, не задумываясь о смысле сообщения. Такой процесс преобразования сообщения называется кодированием. Обратный процессом кодированию является процесс декодирования. Для того чтобы выполнить кодирование или декодирование, необходимо знать правила перевода одних знаков в другие знаки. Говоря другими словами, надо знать код или шифр.

По мере развития средств появились различные способы кодирования информации. Например, кодирование с помощью азбуки (кода) Морзе (длительный сигнал – тире, короткий сигнал – точка, нет сигнала – пауза), с помощью двоичного кода (нет сигнала – 0, есть сигнал – 1). Кодирование используется для представления информации в такой форме, которая будет наиболее удобна для работы человека или технического устройства. Например, человеку удобно и привычно работать с десятичными числами, а компьютер настроен на работу с двоичными числами. Поэтому десятичное число, введенное с помощью клавиатуры компьютера, кодируется в двоичное число. При выводе числа на экран монитора происходит декодирование из двоичного числа в десятичное число. Кодирование информации необходимо не только для ее рационального представления, но и для ее эффективной защиты. Не случайно другим примером кода является пин-код сотового телефона или банковской карточки, а также код, используемый в качестве ключа от цифрового замка дорожной сумки.

Источник

Количество информации способы представления информации

Измерение информации: содержательный и алфавитный подходы. Единицы измерения информации.

Вопрос: «Как измерить информацию?» очень непростой. Ответ на него зависит от того, что понимать под информацией. Но поскольку определять информацию можно по-разному, то и способы измерения тоже могут быть разными.

Содержательный подход к измерению информации.
Для человека информация — это знания человека. Рассмотрим вопрос с этой точки зрения.
Получение новой информации приводит к расширению знаний. Если некоторое сообщение приводит к уменьшению неопределенности нашего знания, то можно говорить, что такое сообщение содержит информацию.
Отсюда следует вывод, что сообщение информативно (т.е. содержит ненулевую информацию), если оно пополняет знания человека. Например, прогноз погоды на завтра — информативное сообщение, а сообщение о вчерашней погоде неинформативно, т.к. нам это уже известно.
Нетрудно понять, что информативность одного и того же сообщения может быть разной для разных людей. Например: «2×2=4» информативно для первоклассника, изучающего таблицу умножения, и неинформативно для старшеклассника.
Но для того чтобы сообщение было информативно оно должно еще быть понятно. Быть понятным, значит быть логически связанным с предыдущими знаниями человека. Определение «значение определенного интеграла равно разности значений первообразной подынтегральной функции на верхнем и на нижнем пределах», скорее всего, не пополнит знания и старшеклассника, т.к. оно ему не понятно. Для того, чтобы понять данное определение, нужно закончить изучение элементарной математики и знать начала высшей.
Получение всяких знаний должно идти от простого к сложному. И тогда каждое новое сообщение будет в то же время понятным, а значит, будет нести информацию для человека.
Сообщение несет информацию для человека, если содержащиеся в нем сведения являются для него новыми и понятными.

Алфавитный подход к измерению информации.

А теперь познакомимся с другим способом измерения информации. Этот способ не связывает количество информации с содержанием сообщения, и называется он алфавитным подходом.
При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Все множество используемых в языке символов будем традиционно называть алфавитом. Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, то мы их тоже включим в алфавит. В алфавит также следует включить и пробел, т.е. пропуск между словами.
Полное количество символов алфавита принято называть мощностью алфавита. Будем обозначать эту величину буквой N. Например, мощность алфавита из русских букв и отмеченных дополнительных символов равна 54.
При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
При использовании двоичной системы (алфавит состоит из двух знаков: 0 и 1) каждый двоичный знак несет 1 бит информации. Интересно, что сама единица измерения информации «бит» получила свое название от английского сочетания «binary digit» — «двоичная цифра».

1 бит — это минимальная единица измерения информации!

Один символ алфавита «весит» 8 бит. Причем 8 бит информации — это настолько характерная величина, что ей даже присвоили свое название — байт.

Сегодня очень многие люди для подготовки писем, документов, статей, книг и пр. используют компьютерные текстовые редакторы. Компьютерные редакторы, в основном, работают с алфавитом размером 256 символов.

В любой системе единиц измерения существуют основные единицы и производные от них.

Для измерения больших объемов информации используются следующие производные от байта единицы:

Источник

Методы измерения количества информации

Теория к заданию 10 из ЕГЭ по информатике

Информация и ее кодирование

Различные подходы к определению понятия «информация». Виды информационных процессов. Информационный аспект в деятельности человека

Информация (лат. informatio — разъяснение, изложение, набор сведений) — базовое понятие в информатике, которому нельзя дать строгого определения, а можно только пояснить:

информация — это новые факты, новые знания;
информация — это сведения об объектах и явлениях окружающей среды, которые повышают уровень осведомленности человека;
информация — это сведения об объектах и явлениях окружающей среды, которые уменьшают степень неопределенности знаний об этих объектах или явлениях при принятии определенных решений.

Понятие «информация» является общенаучным, т. е. используется в различных науках: физике, биологии, кибернетике, информатике и др. При этом в каждой науке данное понятие связано с различными системами понятий. Так, в физике информация рассматривается как антиэнтропия (мера упорядоченности и сложности системы). В биологии понятие «информация» связывается с целесообразным поведением живых организмов, а также с исследованиями механизмов наследственности. В кибернетике понятие «информация» связано с процессами управления в сложных системах.

Основными социально значимыми свойствами информации являются:

полезность;
доступность (понятность);
актуальность;
полнота;
достоверность;
адекватность.

В человеческом обществе непрерывно протекают информационные процессы: люди воспринимают информацию из окружающего мира с помощью органов чувств, осмысливают ее и принимают определенные решения, которые, воплощаясь в реальные действия, воздействуют на окружающий мир.

Информационный процесс — это процесс сбора (приема), передачи (обмена), хранения, обработки (преобразования) информации.

Сбор информации — это процесс поиска и отбора необходимых сообщений из разных источников (работа со специальной литературой, справочниками; проведение экспериментов; наблюдения; опрос, анкетирование; поиск в информационно-справочных сетях и системах и т. д.).

Передача информации — это процесс перемещения сообщений от источника к приемнику по каналу передачи. Информация передается в форме сигналов — звуковых, световых, ультразвуковых, электрических, текстовых, графических и др. Каналами передачи могут быть воздушное пространство, электрические и оптоволоконные кабели, отдельные люди, нервные клетки человека и т. д.

Хранение информации — это процесс фиксирования сообщений на материальном носителе. Сейчас для хранения информации используются бумага, деревянные, тканевые, металлические и другие поверхности, кино- и фотопленки, магнитные ленты, магнитные и лазерные диски, флэш-карты и др.

Обработка информации — это процесс получения новых сообщений из имеющихся. Обработка информации является одним из основных способов увеличения ее количества. В результате обработки из сообщения одного вида можно получить сообщения других видов.

Защита информации — это процесс создания условий, которые не допускают случайной потери, повреждения, изменения информации или несанкционированного доступа к ней. Способами защиты информации являются создание ее резервных копий, хранение в защищенном помещении, предоставление пользователям соответствующих прав доступа к информации, шифрование сообщений и др.

Язык как способ представления и передачи информации

Для того чтобы сохранить информацию и передать ее, с давних времен использовались знаки.

В зависимости от способа восприятия знаки делятся на:

зрительные (буквы и цифры, математические знаки, музыкальные ноты, дорожные знаки и др.);
слуховые (устная речь, звонки, сирены, гудки и др.);
осязательные (азбука Брайля для слепых, жесты-касания и др.);
обонятельные;
вкусовые.

Для долговременного хранения знаки записывают на носители информации.

Для передачи информации используются знаки в виде сигналов (световые сигналы светофора, звуковой сигнал школьного звонка и т. д.).

По способу связи между формой и значением знаки делятся на:

иконические — их форма похожа на отображаемый объект (например, значок папки «Мой компьютер» на «Рабочем столе» компьютера);
символы — связь между их формой и значением устанавливается по общепринятому соглашению (например, буквы, математические символы ∫, ≤, ⊆, ∞; символы химических элементов).

Для представления информации используются знаковые системы, которые называются языками. Основу любого языка составляет алфавит — набор символов, из которых формируется сообщение, и набор правил выполнения операций над символами.

Языки делятся на:

естественные (разговорные) — русский, английский, немецкий и др.;
формальные — встречающиеся в специальных областях человеческой деятельности (например, язык алгебры, языки программирования, электрических схем и др.)

Системы счисления также можно рассматривать как формальные языки. Так, десятичная система счисления — это язык, алфавит которого состоит из десяти цифр 0..9, двоичная система счисления — язык, алфавит которого состоит из двух цифр — 0 и 1.

Методы измерения количества информации: вероятностный и алфавитный

Единицей измерения количества информации является бит. 1 бит — это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.

Связь между количеством возможных событий N и количеством информации I определяется формулой Хартли:

Например, пусть шарик находится в одной из четырех коробок. Таким образом, имеется четыре равновероятных события (N = 4). Тогда по формуле Хартли 4 = 2 I . Отсюда I = 2. То есть сообщение о том, в какой именно коробке находится шарик, содержит 2 бита информации.

При алфавитном подходе к определению количества информации отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка (алфавит) можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет каждый символ:

Например, в русском языке 32 буквы (буква ё обычно не используется), т. е. количество событий будет равно 32. Тогда информационный объем одного символа будет равен:

I = log₂ 32 = 5 битов.

Если N не является целой степенью 2, то число log₂N не является целым числом, и для I надо выполнять округление в большую сторону. При решении задач в таком случае I можно найти как log₂N’, где N′ — ближайшая к N степень двойки — такая, что N′ > N.

Например, в английском языке 26 букв. Информационный объем одного символа можно найти так:

N = 26; N’ = 32; I = log₂N’ = log₂(2 5 ) = 5 битов.

Если количество символов алфавита равно N, а количество символов в записи сообщения равно М, то информационный объем данного сообщения вычисляется по формуле:

Примеры решения задач

Пример 1. Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний («включено» или «выключено»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

Решение. С помощью n лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 n сигналов. 2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит.

Пример 2. Метеорологическая станция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

Решение. В данном случае алфавитом является множество целых чисел от 0 до 100. Всего таких значений 101. Поэтому информационный объем результатов одного измерения I = log₂101. Это значение не будет целочисленным. Заменим число 101 ближайшей к нему степенью двойки, большей 101. Это число 128 = 27. Принимаем для одного измерения I = log₂128 = 7 битов. Для 80 измерений общий информационный объем равен:

80 · 7 = 560 битов = 70 байтов.

Ответ: 70 байтов.

Вероятностный подход к измерению количества информации применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

где $I$ — количество информации;

$N$ — количество возможных событий;

$p_i$ — вероятность $i$-го события.

Например, пусть при бросании несимметричной четырехгранной пирамидки вероятности отдельных событий будут равны:

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

Единицы измерения количества информации

Наименьшей единицей информации является бит (англ. binary digit (bit) — двоичная единица информации).

Бит — это количество информации, необходимое для однозначного определения одного из двух равновероятных событий. Например, один бит информации получает человек, когда он узнает, опаздывает с прибытием нужный ему поезд или нет, был ночью мороз или нет, присутствует на лекции студент Иванов или нет и т. д.

В информатике принято рассматривать последовательности длиной 8 битов. Такая последовательность называется байтом.

Производные единицы измерения количества информации:

1 байт = 8 битов

1 килобайт (Кб) = 1024 байта = 2 10 байтов

1 мегабайт (Мб) = 1024 килобайта = 2 20 байтов

1 гигабайт (Гб) = 1024 мегабайта = 2 30 байтов

1 терабайт (Тб) = 1024 гигабайта = 2 40 байтов

Процесс передачи информации. Виды и свойства источников и приемников информации. Сигнал, кодирование и декодирование, причины искажения информации при передаче

Информация передается в виде сообщений от некоторого источника информации к ее приемнику посредством канала связи между ними.

В качестве источника информации может выступать живое существо или техническое устройство. Источник посылает передаваемое сообщение, которое кодируется в передаваемый сигнал.

Сигнал — это материально-энергетическая форма представления информации. Другими словами, сигнал — это переносчик информации, один или несколько параметров которого, изменяясь, отображают сообщение. Сигналы могут быть аналоговыми (непрерывными) или дискретными (импульсными).

Сигнал посылается по каналу связи. В результате в приемнике появляется принимаемый сигнал, который декодируется и становится принимаемым сообщением.

Передача информации по каналам связи часто сопровождается воздействием помех, вызывающих искажение и потерю информации.

Примеры решения задач

Пример 1. Для кодирования букв А, З, Р, О используются двухразрядные двоичные числа 00, 01, 10, 11 соответственно. Этим способом закодировали слово РОЗА и результат записали шестнадцатеричным кодом. Указать полученное число.

Решение. Запишем последовательность кодов для каждого символа слова РОЗА: 10 11 01 00. Если рассматривать полученную последовательность как двоичное число, то в шестнадцатеричном коде оно будет равно: 1011 0100₂ = В4₁₆.

Скорость передачи информации и пропускная способность канала связи

Прием/передача информации может происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации, или скорость информационного потока.

Скорость выражается в битах в секунду (бит/с) и кратных им Кбит/с и Мбит/с, а также в байтах в секунду (байт/с) и кратных им Кбайт/с и Мбайт/с.

Максимальная скорость передачи информации по каналу связи называется пропускной способностью канала.

Примеры решения задач

Пример 1. Скорость передачи данных через ADSL-соединение равна 256000 бит/с. Передача файла через данное соединение заняла 3 мин. Определите размер файла в килобайтах.

Решение. Размер файла можно вычислить, если умножить скорость передачи информации на время передачи. Выразим время в секундах: 3 мин = 3 ⋅ 60 = 180 с. Выразим скорость в килобайтах в секунду: 256000 бит/с = 256000 : 8 : 1024 Кбайт/с. При вычислении размера файла для упрощения расчетов выделим степени двойки:

Размер файла = (256000 : 8 : 1024) ⋅ (3 ⋅ 60) = (2 8 ⋅ 10 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = (2 8 ⋅ 125 ⋅ 2 3 : 2 3 : 2 10 ) ⋅ (3 ⋅ 15 ⋅ 2 2 ) = 125 ⋅ 45 = 5625 Кбайт.

Ответ: 5625 Кбайт.

Представление числовой информации. Сложение и умножение в разных системах счисления

Представление числовой информации с помощью систем счисления

Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.

Система счисления — это система записи чисел с помощью определенного набора цифр.

Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.

Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.

Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.

Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.

Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.

Например: 8527 = 8 ⋅ 10 3 + 5 ⋅ 10 2 + 2 ⋅ 10 1 + 7 ⋅ 10 0 .

Развернутая форма записи чисел произвольной системы счисления имеет вид

$a$ — цифры численной записи, соответствующие разрядам;

$m$ — количество разрядов числа дробной части;

$n$ — количество разрядов числа целой части;

$q$ — основание системы счисления.

Например, запишем развернутую форму десятичного числа $327.46$:

Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.

Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В₁₂ можно расписать так:

7А,5В₁₂ = В ⋅ 12 -2 + 5 ⋅ 2 -1 + А ⋅ 12 0 + 7 ⋅ 12 1 .

В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.

Перевод чисел в позиционных системах счисления

Перевод чисел из произвольной системы счисления в десятичную

Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:

1101₂ = 1 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 2 1 + 1 ⋅ 2 0 = 13₁₀;

17D,ECH = 12 ⋅ 16 –2 + 14 ⋅ 16 –1 + 13 ⋅ 160 + 7 ⋅ 16 1 + 1 ⋅ 16 2 = 381,921875.

Перевод чисел из десятичной системы счисления в заданную

Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

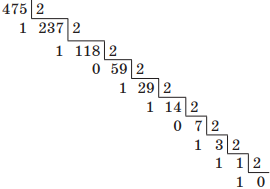
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:

Читая остатки от деления снизу вверх, получим 111011011.

1 ⋅ 2 8 + 1 ⋅ 2 7 + 1 ⋅ 2 6 + 0 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 475₁₀.

Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.

Например, переведем десятичную дробь 0,375₁₀ в двоичную систему счисления:

Полученный результат — 0,011₂.

Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно

Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2 І ; І = 3).

Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.

1234,777₈ = 001 010 011 100,111 111 111₂ = 1 010 011 100,111 111 111₂;

1234567₈ = 001 010 011 100 101 110 111₂ = 1 010 011 100 101 110 111₂.

При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.

Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2 І ; І = 4).

Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.

Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.

1234,AB77₁₆ = 0001 0010 0011 0100,1010 1011 0111 0111₂ = 1 0010 0011 0100,1010 1011 0111 0111₂;

CE4567₁₆ = 1100 1110 0100 0101 0110 0111₂.

При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.

Например, переведем троичное число 211₃ в семеричную систему счисления. Для этого сначала преобразуем число 211₃ в десятичное, записав его развернутую форму:

211₃ = 2 ⋅ 3 2 + 1 ⋅ 3 1 + 1 ⋅ 3 0 = 18 + 3 + 1 = 22₁₀.

Затем переведем десятичное число 22₁₀ в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:

Примеры решения задач

Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.

Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 12₁₀ = 110_n = 0 ·n 0 + 1 · n 1 + 1 · n 2 . Составим уравнение: n 2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 110₃ = 0· 3 0 + 1 · 3 1 + 1 · 3 2 = 0 + 3 + 9 = 12 .

Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.

Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 22₁₀ = 34₆ = 24₉ = 14₁₈.

Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.

Решение. Для удобства воспользуемся восьмеричной системой счисления. 101₂ = 5₈. Тогда число х можно представить как x = 5 · 8 0 + a₁ · 8 1 + a₂ · 8 2 + a₃ · 8 3 + . , где a₁, a₂, a₃, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 8 2 > 25), т. е. такие числа должны иметь представление x = 5 + a₁ · 8. Поскольку x ≤ 25 , допустимыми значениями a₁ будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:

a₁ = 0; x = 5 + 0 · 8 = 5;.

a₁=1; x = 5 + 1 · 8 = 13;.

a₁ = 2; x = 5 + 2 · 8 = 21;.

Арифметические операции в позиционных системах счисления

Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.

Сложение	Вычитание	Умножение
0 + 0 = 0	0 – 0 = 0	0 ⋅ 0 = 0
0 + 1 = 1	1 – 0 = 1	0 ⋅ 1 = 0
1 + 0 = 1	1 – 1 = 0	1 ⋅ 0 = 0
1 + 1 = 10	10 – 1 = 1	1 ⋅ 1 = 1

Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.

Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:

Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:

Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:

Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.

Например, выполним сложение восьмеричных чисел 36₈ и 15₈, а также вычитание шестнадцатеричных чисел 9С₁₆ и 67₁₆:

При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.

Представление чисел в компьютере

Формат с фиксированной запятой

В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.

Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно

1 ⋅ 2 7 + 1 ⋅ 2 6 + 1 ⋅ 2 5 + 1 ⋅ 2 4 + 1 ⋅ 2 3 + 1 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 255₁₀.

Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.

Для п-разрядного представления диапазон будет составлять от 0 до 2 n – 1.

Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.

Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2 n − |А|.

Алгоритм получения дополнительного кода отрицательного числа:

1. Записать прямой код числа в п двоичных разрядах.

2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)

3. Прибавить единицу к полученному обратному коду.

Например, получим дополнительный код числа –2014₁₀ для шестнадцатиразрядного представления:

Прямой код	Двоичный код числа 2014₁₀ со знаковым разрядом	1000011111011110
Обратный код	Инвертирование (исключая знаковый разряд)	1111100000100001
Прибавление единицы	1111100000100001 + 0000000000000001
Дополнительный код	1111100000100010

При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.

1) Найдем разность 13₁₀ – 12₁₀ для восьмибитного представления. Представим заданные числа в двоичной системе счисления:

Запишем прямой, обратный и дополнительный коды для числа –12₁₀ и прямой код для числа 13₁₀ в восьми битах:

13₁₀	–12₁₀
Прямой код	00001101	10001100
Обратный код	—	11110011
Дополнительный код	—	11110100

Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):

Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.

2) Найдем разность 8₁₀ – 13₁₀ для восьмибитного представления.

Запишем прямой, обратный и дополнительный коды для числа –13₁₀ и прямой код для числа 8₁₀ в восьми битах:

8₁₀	–13₁₀
Прямой код	00001000	10001101
Обратный код	—	11110010
Дополнительный код	—	11110011

Вычитание заменим сложением:

В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:

11111011 – 00000001 = 11111010.

Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –5₁₀.

Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2 n–1 , а максимальное: |А| = 2 n–1 или А = –2 n–1 – 1.

Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно

А = –2 31 = –2147483648₁₀.

Максимальное положительное число равно

А = 2 31 – 1 = 2147483647₁₀.

Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.

Формат с плавающей запятой

Вещественные числа хранятся и обрабатываются в компьютере в формате с плавающей запятой, использующем экспоненциальную форму записи чисел.

Число в экспоненциальном формате представляется в таком виде:

где $m$ — мантисса числа (правильная отличная от нуля дробь);

$q$ — основание системы счисления;

$n$ — порядок числа.

Например, десятичное число 2674,381 в экспоненциальной форме запишется так:

2674,381 = 0,2674381 ⋅ 10 4 .

Число в формате с плавающей запятой может занимать в памяти 4 байта (обычная точность) или 8 байтов (двойная точность). При записи числа выделяются разряды для хранения знака мантиссы, знака порядка, порядка и мантиссы. Две последние величины определяют диапазон изменения чисел и их точность.

Определим диапазон (порядок) и точность (мантиссу) для формата чисел обычной точности, т. е. четырехбайтных. Из 32 битов 8 выделяется для хранения порядка и его знака и 24 — для хранения мантиссы и ее знака.

Найдем максимальное значение порядка числа. Из 8 разрядов старший разряд используется для хранения знака порядка, остальные 7 — для записи величины порядка. Значит, максимальное значение равно 1111111₂ = 127₁₀. Так как числа представляются в двоичной системе счисления, то

Аналогично, максимальное значение мантиссы равно

Таким образом, диапазон чисел обычной точности составляет $±1.7 · 10^<38>$.

Кодирование текстовой информации. Кодировка ASCII. Основные используемые кодировки кириллицы

Соответствие между набором символов и набором числовых значений называется кодировкой символа. При вводе в компьютер текстовой информации происходит ее двоичное кодирование. Код символа хранится в оперативной памяти компьютера. В процессе вывода символа на экран производится обратная операция — декодирование, т. е. преобразование кода символа в его изображение.

Присвоенный каждому символу конкретный числовой код фиксируется в кодовых таблицах. Одному и тому же символу в разных кодовых таблицах могут соответствовать разные числовые коды. Необходимые перекодировки текста обычно выполняют специальные программы-конверторы, встроенные в большинство приложений.

Как правило, для хранения кода символа используется один байт (восемь битов), поэтому коды символов могут принимать значение от 0 до 255. Такие кодировки называют однобайтными. Они позволяют использовать 256 символов ( N = 2 I = 2 8 = 256 ). Таблица однобайтных кодов символов называется ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Первая часть таблицы ASCII-кодов (от 0 до 127) одинакова для всех IBM-PC совместимых компьютеров и содержит:

коды управляющих символов;
коды цифр, арифметических операций, знаков препинания;
некоторые специальные символы;
коды больших и маленьких латинских букв.

Вторая часть таблицы (коды от 128 до 255) бывает различной в различных компьютерах. Она содержит коды букв национального алфавита, коды некоторых математических символов, коды символов псевдографики. Для русских букв в настоящее время используется пять различных кодовых таблиц: КОИ-8, СР1251, СР866, Мас, ISO.

В последнее время широкое распространение получил новый международный стандарт Unicode. В нем отводится по два байта (16 битов) для кодирования каждого символа, поэтому с его помощью можно закодировать 65536 различных символов ( N = 2 16 = 65536 ). Коды символов могут принимать значение от 0 до 65535.

Примеры решения задач

Пример. С помощью кодировки Unicode закодирована следующая фраза:

Я хочу поступить в университет!

Оценить информационный объем этой фразы.

Решение. В данной фразе содержится 31 символ (включая пробелы и знак препинания). Поскольку в кодировке Unicode каждому символу отводится 2 байта памяти, для всей фразы понадобится 31 ⋅ 2 = 62 байта или 31 ⋅ 2 ⋅ 8 = 496 битов.

Источник