Когерентность. Способы получения когерентных пучков
В повседневной жизни явление интерференции не наблюдается (светлые и темные полосы). Что же такое когерентность?
Когерентность – согласованное протекание нескольких колебательных процессов.
Характеристики волны: амплитуда, частота и фаза. У когерентных волн разность фаз постоянна (см. выше). Эти характеристики для таких волн могут быть или изменяемы или постоянны. Но с изменением равным константе.
Все зависит от времени. Величина меняется хаотически. При рассмотрении интенсивности света мы (***) среднем определяем промежуток времени.
Для наблюдения интерференции необходимы когерентные источники. Какие есть способы получения когерентных источников?
— синусоидальная волна абсолютная математическая абстракция.
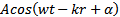
(w — круговая частота, k – волновой вектор, х – координата (т.к. свет можно рассматривать в одномерном пространстве); k = w/v). В реальности атомы излучают несколько кусочков синусоиды и согласно принципу неопределенности, каждый атом излучает эту частичку в неком диапазоне частот: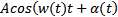 
. 
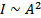
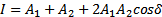
— интенсивность света пропорциональна квадрату амплитуды. 
.
Если бы наш глаз мог регистрировать картинки с временным разрешением 10 -10 , то у нас рябило бы в глазах. Глаз усредняет картинку 0,1 с. Физический прибор имеет время регистрации дельта t. Если за 0,1 с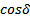 
пробегает все значения от -1 до 1 и не один раз, то при усреднении получится 0. Помимо того, что этот cos принимает разные значения, есть еще и разные значения волн.
Время когерентности – время за которое изменение достигает пи.
Длина когерентности —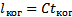 
.
На этих знаниях основаны способы получения когерентных пучков:
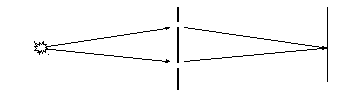
1. Метод деления волнового фронта основан на использовании двух экранов. Как поставить линзу и источник, чтобы получился луч падающий на экран. Дельта х должно быть меньше длины когерентности.
2. Метод деления амплитуды основан на отражении света в мелкой пластинке. Исходная волна 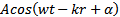разделилась амплитуда и снова деления многочисленные.
Источник
Способы получения когерентных источников света
Когерентные источники света – это источники, которые имеют постоянную во времени разность фаз, согласованное протекание нескольких колебательных или волновых процессов, степень которых различна.
Имеется много способов получения когерентных источников света, но суть их одинакова. С помощью разделения пучка на две части получают два мнимых источника света, дающих когерентные волны.
Интерференция света – сложение двух или нескольких световых волн с одинаковыми периодами, сходящихся в одной точке, в результате которого наблюдается увеличение или уменьшение амплитуда результирующей волны. Для получения устойчивой интерференционной картины необходимо, чтобы складываемые волны были когерентны. Когерентными называют волны с одинаковой частотой (периодом) и постоянной во времени разностью фаз. Чтобы получить когерентные волны необходимо световую волну от одного источника разделить на две или несколько волн. После прохождения различных путей эти волны, имея некоторую разность хода, интерферируют.
Приёмы разделения волны:
· С помощью бипризмы Френеля:
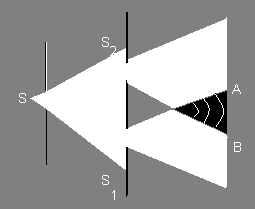
Волна, идущая от источника света, раздваивается из-за преломления света в двух половинах бипризмы. Получаемы волны 1 и 2 как бы исходят от двух мнимых источников S1 и S2 и являются когерентными, поэтому в заштрихованной области наблюдается интерференция.
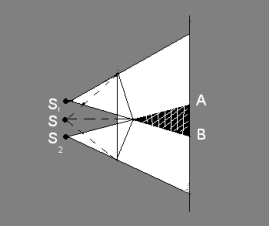
Свет, проходящий через узкое отверстие S, падает на экран с двумя отверстиями S1 и S2 и делится на две когерентных волны, поэтому в заштрихованной области наблюдается интерференция, а на экране – интерференционная картина.
2. Вывод выражения для расстояния l между мнимыми изображения источника в случае бипризмы.
Бипризма Френеля представляет собой изготовленные из одного куска стекла две симметричные призмы, имеющие общее основание и малый преломляющий угол G≈1°. На расстоянии L1 от бипризмы располагается источник света S. Можно показать, что в этом случае, если преломляющий угол призмы мал и лучи падают на призму под небольшими углами, все лучи отклоняются призмой почти на одинаковый угол ϕ, равный
где n – показатель преломления стекла, из которого изготовлена призма, α – преломляющий угол каждой половинки бипризмы. При этом мнимые изображения S1 и S2 точечного источника света S лежат с ним в одной плоскости. В результате образуются две когерентные волны, исходящие из мнимых источников S1 и S2. Расстояние d между мнимыми источниками равно:
где L1 – расстояние между источником S и бипризмой. При этом, sin ϕ≈ϕ (так как угол ϕ достаточно мал), тогда:
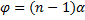
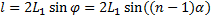
Источник
3) Когерентность и способы её осуществления.
Рассмотрим случай, когда в одну и ту же точку одновременно придут две электромагнитные волны. Рассмотрим простейший случай, когда частоты волн одинаковы и направления векторов Е также одинаковы. Тогда модуль результирующего вектора подсчитывается по формуле:
В естественном источнике свет излучается множеством атомов. Рассмотрим один атом. Отдельный атом излучает свет в среднем в течение времени с. За это время свет проходит расстояние, равное l = c м/с * 1*10 -8 с = 3 м.
Иными словами, если свет от одного атома оптическим путём разделить на два луча, а затем свести их в одну точку, то в данной точке будет наблюдаться устойчивая картина максимума или минимума. Но это будет наблюдаться только тогда, если разность хода этих лучей не будет превышать этих 3-х метров. В противном случае, в эту точку придут лучи от разных атомов и устойчивой картины не будет.
В естественном источнике света свет излучается множеством атомов и их, конечно, невозможно заставить излучать свет в строгом согласовании друг с другом. Поэтому, для получения устойчивой картины максимумов и минимумов, существует единственный способ: нужно оптическим путём разделить источник света на два источника (действительных или мнимых) и свести эти лучи в одну точку. Тогда будет в этой точке наблюдаться устойчивая картина максимума или минимума. В данном случае, источники света будут излучать свет в строгом соответствии друг с другом и они будут называться когерентными. Какими способами это можно осуществить?
а) способ Ллойда (рис.3.1) На экран в одну точку падают два луча: один – сразу от источника, другой – отражённый от зеркала под очень пологим углом:
б) способ Френеля (рис.4.1) На экране в одной точке встречаются два луча, прошедшие через обе слабо преломляющие грани двойной призмы (бипризмы Френеля)
в) способ Юнга (рис.5.1)
в) способ Юнга (рис.5.1) На экране встречаются два луча, вышедшие из двух близко расположенных очень узких щелей в непрозрачном экране. В данном случае щели действуют как два когерентных источников света:
4) Сущность интерференции и способы её наблюдения.
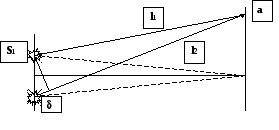
Интерференция – означает сложение (наложение) волн, при котором наблюдается устойчивая картина максимумов и минимумов. Для осуществления интерференции необходимо наличие двух когерентных источников света. Допустим, что мы имеем два источника света : S1 и S2. Они – когерентны, поскольку у них одинаковые частоты и фазы. Для простоты расчётов допустим, что у них одинаковые амплитуды векторов электрического поля. Выберем на экране какую-либо точку а. Расстояние от неё до источников S1 и S2 , соответственно равны l1 и l2 .(рис.6.1)
Тогда уравнение волны от первого источника
Уравнение волны от второго источника:
Поскольку частоты этих источников одинаковые, то волны придут в точку а с разностью фаз:
Здесь — оптическая разность хода.
Для того, чтобы в точке а был максимум, нужно, чтобы в эту точку пришли волны в одной фазе, т.е. или k.
Максимум получается, если разность хода равна целому числу длин волн. А минимум получается, если разность хода равна нечётному числу длин волн. 2k + 1)
Иными словами, на экране будет наблюдаться картина, состоящая из максимумов и минимумов. В центре экрана будет находиться центральный максимум, по обе стороны от него будут находиться максимумы первого порядка, при которых разность хода лучей равна одной длине волны, ещё дальше будут находиться максимумы второго порядка, при которых разность хода будет равна двум длинам волны и т.д. При этом, интерференционная картина будет симметрична относительно центрального максимума.
И чем меньше расстояние между источниками, тем реже друг от друга будут находиться максимумы. А чем меньше будет длина световой волны, тем наоборот: максимумы будут располагаться ближе друг к другу.
Источник
3.6.10 Интерференция света. Когерентные источники
Видеоурок 1: Интерференция света
Видеоурок 2: Задачи на интерференцию света
Лекция: Интерференция света. Когерентные источники. Условия наблюдения максимумов и минимумов в интерференционной картине от двух синфазных когерентных источников
Взаимодействие световых волн
В реальном мире невозможно наблюдать за отдельными лучами, мы видим картину, где несколько лучей взаимодействуют друг с другом, в результате чего она получается именно такой, как мы ее видим.
Для упрощения рассмотрения процессов взаимодействия нескольких световых волн, рассмотрим две волны. Рассматриваемые нами процессы могут происходить с любыми существующими волнами (светом, электромагнитными, механическими и др.).
Все превращения, которые происходят в результате наложения волн, наблюдаются в результате сложения их характеристик (амплитуды, фазы и др.).
Если накладываются две волны с одинаковыми фазами, то они соединяются в одну, с большей амплитудой.
Если же волны приходят в противофазе, то происходит постоянное гашение максимума минимум, в результате чего волна выравнивается.
Когерентность
Представим некоторые источники, от которых исходят волны, имеющие некоторые одинаковые параметры. О чем именно речь? Такие источники должны испускать волны, имеющие одинаковую фазу и постоянную разность фаз. Такие источники называются когерентными, волны, которые они испускают, носят аналогичное название. Аналогичные волны и их графики изображались выше. Теперь мы знаем, что происходит в результате наложения когерентных волн — они либо усиливают друг друга, либо наоборот гасят.
Условия max и min
Кроме перечисленных выше физических величин, важна разность хода.
Для указанных когерентных волн, разностью хода будет разность между отрезками S1P и S2P.
Как можно заметить на рисунке, разность хода между волнами равна длине одной волны — одна имеет три полных длины волны, а вторая — четыре. В точке Р данные волны складываются вместе, а так как мы знаем, что подобное сложение приводит к увеличению амплитуды, то говорят, что наблюдается интерференционный максимум.
Условие максимума: Разность хода волн равна целому числу волн.
Теперь же рассмотрим иную ситуацию сложения двух когерентных волн:
В данном случае фазы отличаются на одинаковое значение, волны находятся в противофазе.
В таком случае наблюдается интерференционный минимум.
Условие минимума: Разность хода равна некоторому количеству полуцелых длин волн.
Интерференция
В результате того, что в некоторых местах наложения волн наблюдается максимум, а в некоторых минимум, появляется интерференционная картина. Однако стоит заметить, что данное явление справедливо только для когерентных волн.
На рисунке изображена интерференция от двух когерентных источников. Как можно заметить на рисунке. Нет конкретного разделения черных и белых полос, существуют промежуточные значения, которые рассматриваются серым цветом. То же можно наблюдать и в результате двух малых источников света — на экране мы будем видеть плавные переходы от черного до белого цвета. Белый — максимум, черный — минимум.
Интерференция в тонких пленках
Все мы наблюдали ситуацию, когда свет, преломляясь на мыльном пузыре, приобретает радужную окраску. Все это происходит в результате интерференции.
Представим себе тонкую прозрачную среду, на которую попадает луч. Как мы знаем, он отражается от нее и преломляется. Как можно заметить, в результате данного процесса выходят два луча. А так как они выпущены от одного источника, то они интерферентны, но с разностью хода. В результате данной разницы хода, белый цвет будет разделяться на цвета радуги, и в зависимости от толщины пленки, выходить будет какой-то один.
Ту же ситуацию можно наблюдать и при соприкосновении стеклышка и линзы.
Если на такую систему пустить монохроматичный свет (например, красный), то в результате получится явление называемого кольцами Ньютона:
Источник
