Когда применяется способ концентрических сфер

Таким образом, если центр сферы находится на оси некоторой поверхности вращения, то эта поверхность пересекается со сферой по окружностям. Это свойство и положено в основу способа вспомогательных сфер.

Способ концентрических сфер следует применять в случаях, когда соблюдаются следующие три условия:

·пересекаются поверхности вращения или поверхности, содержащие семейства окружностей, по которым их могут пересекать концентрические сферы;

·оси поверхностей вращения пересекаются;

·поверхности имеют общую плоскость симметрии, параллельную одной из плоскостей проекций. Если же она не параллельна ни одной из плоскостей проекций, то необходимо произвести преобразование чертежа для достижения необходимых условий решения.

Пример 1. Построить линию пересечения конуса вращения с цилиндром вращения (рисунок 12-2).

Сначала определим некоторые опорные точки. Так как поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций, то пересечение их контурных образующих в точках А и В определяет высшую и низшую точки линии пересечения.

Центр сфер 0 выбирают в месте пересечения осей цилиндра и конуса, т.к. только в этом случае сферы будут соосны с обеими поверхностями.

Определим радиус минимальной Rmin и максимальной Rmax сфер, которые будем использовать при решении задачи. Rmax определяется расстоянием от точки 0 до самой удаленной опорной точки.

Для определения Rmin необходимо из центра 0 опустить перпендикуляры на очерковые образующие поверхностей из центра 0 опустить перпендикуляры на очерковые образующие поверхностей. Больший из них принимается в качестве Rmin, т.к. сфера такого радиуса будет касаться одной и пересекать вторую поверхность, что дает возможность найти общие для обеих поверхностей точки — точки линии пересечения. При радиусе сферы меньшем Rmin она не будет иметь общих точек с одной из поверхностей; построения теряют смысл.

Для построения случайных точек проводим сферы радиуса Rmin

· каждая поверхность содержит семейство окружностей, по которым её могут пересекать эксцентрические сферы, общие для обеих поверхностей.

Пример 2. Построить линию пересечения конуса вращения со сферой (рисунок12-3).

Плоскостью симметрии данных поверхностей является фронтальная плоскость, поэтому можно применить способ вспомогательных сфер. Каких?

Задачу можно решить как способом концентрических сфер, так и эксцентрических. Решим её вторым способом.

Центр сфер можно брать в любой точке оси конуса вращения. На рисунке 12-3 проведены три сферы радиусов RI, R2, R3. Каждая из этих сфер пересекается с каждой из данных поверхностей по окружности, точки пересечения которых будут точками линии пересечения.

На виде сверху точки находим с помощью параллелей конуса h¹,h²,h³.

Пример 2.Построить линию пересечения конуса вращения с тором (рисунок 12-4).

Эту задачу можно решить только способом эксцентрических сфер.

Обе поверхности имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций, в которой расположены ось конуса и линия центров тора.

Как и во всех задачах на пересечение поверхностей, вначале определяем опорные точки. Самая верхняя и правая — т. А, расположенная на пересечении контурных линий. Чтобы найти нижнюю и левую т. В (точку касания контурных линий конуса и тора), необходимо из т. О опустить перпендикуляр на контурную образующую конуса; их пересечение определяет т.В.

Для построения дополнительных точек выделим одну окружность–m принадлежащую поверхности тора.

Центры всех сфер, которые будут пересекаться с тором по этой окружности, будут лежать на прямой n1 данной окружности C1 перпендикулярно к её плоскости. Эта прямая пересечёт ось конуса (т.к. они лежат в одной плоскости) в т. 01. Эта точка будет центром сферы, которая пересечёт поверхность конуса по окружности h1. Окружности m1 и h1 пересекаются в точках 1 и 2, которые будут принадлежать линии пересечения.

Для нахождения дополнительных точек нужно взять новую окружность на поверхности тора и все действия повторить.

На виде сверху точки линии пересечения находят при помощи параллелей конуса h .

Источник

Когда применяется способ концентрических сфер

Контрольные задания по теме:
Рабочая тетрадь задача 75, задача 76

Этот метод вытекает из свойств, присущих поверхностям вращения: если центр секущей сферы находится на оси поверхности вращения, то сфера пересечет данную поверхность по окружностям, число которых равно числу точек пересечения главных меридианов поверхностей. На рисунке 54 показано сечение конуса и цилиндра вспомогательной сферой.

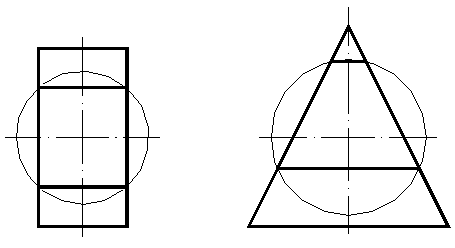
Рисунок 54

Способ сфер применяется в особом случае, когда поверхности вращения расположены так, что их оси пересекаются и параллельны одной из плоскости проекций.

Построение линии пересечения поверхностей вращения с помощью вспомогательных секущих сфер возможно двумя способами:

1) способом концентрических сфер;

2) способом эксцентрических сфер.

Первый применяется тогда, когда оси поверхностей — прямые линии, а второй — когда одна из осей является кривой.

Рассмотрим пример пересечения двух цилиндров разного радиуса. Оси их пересекаются и параллельны фронтальной плоскости проекций. Поверхности изображены на рисунке 55.

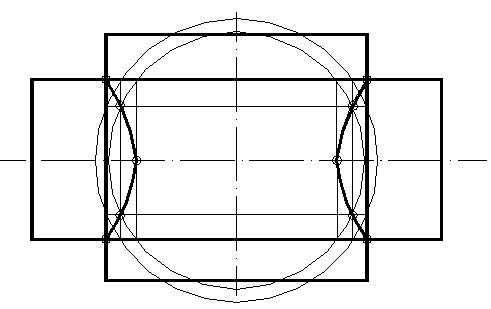
Рисунок 55

Первая сфера проводится так, чтобы она была вписана в поверхность большего диаметра, последующие сферы пересекают обе поверхности, а радиус последней сферы равен расстоянию до точек пересечения очерков.

Вспомогательные сферы пересекают цилиндры по окружностям, которые проецируются в прямые линии, проходящие через точки пересечения сфер с очерками цилиндров. Точки пересечения этих прямых и есть общие точки для двух поверхностей.

При построении линии пересечения этим способом все сферы проводятся из одного центра, которым является точка пересечения осей. В способе эксцентрических сфер центр секущей сферы передвигается вдоль оси поверхности, ось которой прямолинейна.

Если две пересекающиеся поверхности вращения можно описать вокруг третьей, то линия пересечения в этом случае распадется на две плоские кривые. Примеры такого пересечения приведены на рисунке 56.

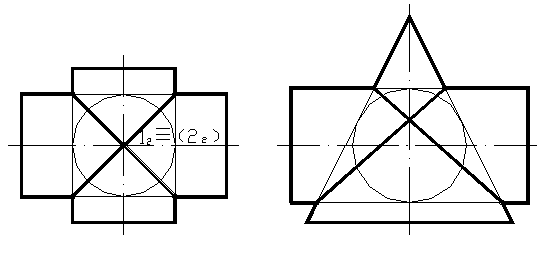
Рисунок 56

В рассмотренных примерах имеет место двойное соприкасание пересекающихся поверхностей второго порядка. Эти поверхности могут быть описаны вокруг одной сферы. Данный случай относится к частным случаям взаимного пересечения поверхностей и описывается теоремой Монжа: две поверхности второго порядка, описанные около третьей поверхности второго порядка (или в нее вписанные), пересекаются между собой по двум кривым второго порядка, плоскости которых проходят через прямую, соединяющую точки пересечения линий касания.

1. Какое свойство поверхностей вращения лежит в основе способа сфер?

2. При каком расположении поверхностей возможно применение способа сфер для построения линии их взаимного пересечения?

3. В каком случае следует применять метод эксцентрических сфер, а в каком – концентрических?

4. Какие частные случаи пересечения поверхностей вы знаете?

5. Сформулируйте теорему Монжа.

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Когда применяется способ концентрических сфер

Этот способ применяется для построения линии пересечения поверхностей вращения произвольного вида, при условии, что оси этих поверхностей пересекаются.

В основу способа концентрических сфер положено свойство сферы с центром на оси какой-либо поверхности.

Если центр сферы находится на оси какой-нибудь поверхности вращения, то сфера соосна с поверхностью вращения и в их пересечении получатся окружности (рис. 106).

Рассмотрим способ концентрических сфер на примере построения линии пересечения цилиндра и конуса вращения, оси которых i(i₁,i₂) и q(q₁,q₂) пересекаются и точка пересечения осей обозначена через O(O₁,O₂) (рис. 107).

Точка пересечения осей поверхностей принимается за центр вспомогательных концентрических сфер.

Алгоритм решения задачи об определении линии пересечения поверхностей состоит в следующем:

1. Определить опорные точки (рис. 108). Так как обе данные поверхности имеют общую плоскость симметрии δ(δ₁), параллельную плоскости проекций П₂, то их очерковые образующие, по отношению к плоскости П₂, пересекаются. Точки A(A₁,A₂), B(B₁,B₂), C(C₁,C₂) и D(D₁,D₂) пересечения этих образующих являются точками видимости линии пересечения поверхностей.

2. Определить радиусы максимальной и минимальной сфер, необходимых для определения точек линии пересечения.

Радиус максимальной сферы R_max равен расстоянию от центра вспомогательных сфер до наиболее удаленной точки пересечения очерковых образующих, в данном случае R_max=O₂A₂ (рис. 109).

Чтобы определить радиус минимальной сферы R_min, необходимо провести через точку O₂ нормали к очерковым образующим данных поверхностей. Тогда больший из отрезков этих нормалей и будет R_min. В этом случае сфера минимального радиуса будет касаться одной из данных поверхностей, а со второй – пересекаться.

В данном случае сферой минимального радиуса является сфера, касающаяся цилиндрической поверхности (см. рис. 109).

Сфера радиусом R_min касается цилиндрической поверхности по окружности m, которая на фронтальной проекции изображается в виде прямой m₂), перпендикулярной q₂) (m₂)⊥q₂)). Эта же сфера пересекает коническую поверхность по двум окружностям. Но, в данном случае, нам интересна только окружность n, так как только она дает решение. Эта окружность n изображается на фронтальной проекции в виде прямой n₂), перпендикулярной i₂)(n₂)⊥i₂)). Точки E и F пересечения этих окружностей будут принадлежать обеим поверхностям:

Чтобы построить горизонтальные проекции точек E и F следует воспользоваться окружностью n, содержащей данные точки, так как она не искажается на плоскости проекций П₁:

3. Для построения промежуточных точек линии пересечения проводят несколько концентрических сфер с центром в точке O, причем радиус R этих сфер должен изменяться в пределах R_minmax. Рассмотрим определение точек линии пересечения на примере сферы радиусом R₁ (R_min1max)(рис. 110, 111).

Сфера радиусом R₁ пересекает цилиндрическую поверхность по окружности l, которая на фронтальной проекции изображается в виде прямой l₂, перпендикулярной q₂(l₂⊥q₂). Эта же сфера пересекает коническую поверхность по окружности k, которая изображается на фронтальной проекции в виде прямой k₂, перпендикулярной i₂(k₂⊥i₂). Точки G и H пересечения этих окружностей будут точками искомой линии пересечения:

Чтобы построить горизонтальные проекции точек G и H, следует воспользоваться окружностью k, содержащей данные точки, так как она не искажается на плоскости проекций

4. Аналогичным образом определить все остальные точки искомой линии пересечения. Последовательно соединить полученные точки плавной лекальной кривой. В данном случае линия пересечения поверхностей цилиндра и конуса представляет собой две кривые второго порядка u(u₁,u₂) и u'(u’₁,u’₂) (рис. 112).

Горизонтальная проекция линии пересечения поверхностей симметрична относительно плоскости δ(δ₁) – общей плоскости симметрии данных поверхностей. Эта плоскость была указана ранее (см. рис. 108).

5. Определить видимость линии пересечения поверхностей и их очерковых образующих. На фронтальной плоскости проекций видимы будут те точки линии пересечения, которые лежат перед горизонтальной проекцией очерковых образующих, проекции которых совпадают с плоскостью симметрии δ(δ₁), – точки A, M, G, E, D и B, K, P, C. На горизонтальной плоскости проекций линия u(u₁,u₂)видима, так как все ее точки лежат выше фронтальной проекции оси вращения цилиндра q(q₂), а линия u'(u’₁,u’₂) будет невидима, поскольку все ее точки лежат ниже фронтальной проекции образующих, совпадающих с проекцией оси вращения цилиндра q(q₂).

Источник