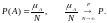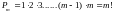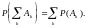- Учебник по теории вероятностей
- 1.3. Геометрическое определение вероятности
- Примеры решений на геометрическую вероятность
- Когда применяется геометрический способ задания вероятности пространство элементарных событий
- Классический способ задания вероятности
- Геометрический способ задания вероятности
- Дискретный способ задания вероятности
- Статистический способ задания вероятности
Учебник по теории вероятностей
1.3. Геометрическое определение вероятности
Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие A – это подмножество этой области, пространства элементарных исходов G.
Если для простоты считать, что все точки G «равноправны» (выбор точек равномерен внутри области), то вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы.
Геометрическая вероятность события А определяется отношением: $$ P(A)=\frac
Чаще всего, в одномерном случае речь будет идти о длинах отрезков, в двумерном — о площадях фигур, в трехмерном — об объемах тел.
При этом, некоторые задачи сразу имеют геометрическую интерпретацию (первый пример), а другие выглядят как задачи «про жизнь», самая распространенная из них — задача о встрече (второй пример).
Основная сложность при решении задач такого типа — построить математическую модель эксперимента, нужным образом выбрать пространство элементарных исходов, обозначить событие, выразить его математически как некоторую область. К сожалению, единого рецепта решения подобых заданий нет, нужно «набить» руку на разных задачах (см. примеры тут, например).
Примеры решений на геометрическую вероятность
Пример. На плоскость, разграфленную параллельными полосами шириной $2d$, расстояние между осевыми линиями которых равно $2D$, наудачу брошен круг радиуса $r$ ($r+d\lt D$). Найти вероятность того, что круг пересечет некоторую полосу.
Решение. В качестве элементарного исхода этого испытания будем считать расстояние $x$ от центра круга до осевой линии ближайшей к кругу полосы (ее обозначим за 0). Тогда все пространство элементарных исходов – это отрезок, равный половине расстояния между осями полос $G=\
Рассмотрим теперь случаи, благоприятствующие событию $A$ = (Круг пересечет полосу), и найдем меру соответствующей области точек. На чертеже выше покажем различные варианты выпадения круга.
Пересечение круга с полосой очевидно произойдет в том случае, если его центр попадет в полосу (точнее, ее половину), т.е. координата центра круга удовлетворяет неравенству $0 \le x \le d$, длина этого отрезка $d$.
Также круг пересечет полосу, если его центр будет находится от края полосы на расстоянии меньшем чем радиус (если равен радиусу — круг коснется полосы, если больше — то отстоит от полосы), т.е. когда $d \le x \le d+r$ (длина этого отрезка $r$).
Тогда вероятность события $A$ по геометрическому определению вероятности: $$ P(A)=\frac
Пример. Два человека договорились встретиться в определенном месте от 17 до 18 часов. При этом каждый обязался после прихода на место встречи ожидать другого 30 минут. Какова вероятность встречи этих людей, если каждый из них равновозможно придет в течение указанного интервала времени?
Решение. Обозначим моменты прихода первого и второго человека за $x$ и $y$. Так как они приходят в промежуток длительности 60 минут (от 17 до 18 часов), то справедливы следующие условия: $0 \le x \le 60$ и $0 \le y \le 60$.
Рассмотрим прямоугольную систему координат $xOy$. В этой системе координат всем возможным значениям времени прихода людей соответствуют точки квадрата со стороной 60.
Лица встретятся, если один человек придет раньше, чем уйдет другой, то есть если $y \lt x+30$, когда $y \gt x$ (второй пришел позже первого, но не позже чем через 30 минут от него) и $x \lt y+30$, когда $y \lt x$ (первый пришел позже второго, не но позже чем через 30 минут).
Более компактно запишем условия $$ x \lt y \lt x+30 \quad \text < или >\quad x-30 \lt y \lt x. \quad (*) $$
Построим прямые $y=x$, $y=x-30$, $y=x+30$ и закрасим область, лежащую внутри квадрата, точки которой удовлетворяют условиям (*). Точки этой фигуры (серый шестиугольник в центре) являются благоприятствующими событию $A$ =(люди встретятся).
Тогда искомая вероятность встречи по геометрическому определению вероятности равна отношению площади этой фигуры к площади квадрата: $$ P=\frac<60^2-1/2\cdot 30^2-1/2\cdot 30^2><60^2>=\frac<3600-900><3600>=\frac<3><4>=0,75. $$
Источник
Когда применяется геометрический способ задания вероятности пространство элементарных событий
оЕ ЧУЕ УМХЮБКОЩЕ СЧМЕОЙС (ЬЛУРЕТЙНЕОФЩ) НПЦОП ЙЪХЮБФШ НЕФПДБНЙ ФЕПТЙЙ ЧЕТПСФОПУФЕК, Б МЙЫШ ФЕ, ЛПФПТЩЕ НПЗХФ ВЩФШ ЧПУРТПЙЪЧЕДЕОЩ Ч ПДОЙИ Й ФЕИ ЦЕ ХУМПЧЙСИ. уМХЮБКОПУФШ Й ИБПУ ОЕ ПДОП Й ФП ЦЕ. пЛБЪЩЧБЕФУС, ЮФП Й Ч УМХЮБКОЩИ ЬЛУРЕТЙНЕОФБИ ОБВМАДБАФУС ОЕЛПФПТЩЕ ЪБЛПОПНЕТОПУФЙ, ОБРТЙНЕТ УЧПКУФЧП «УФБФЙУФЙЮЕУЛПК ХУФПКЮЙЧПУФЙ» : ЕУМЙ ОЕЛПФПТПЕ УПВЩФЙЕ, НПЗХЭЕЕ РТПЙЪПКФЙ ЙМЙ ОЕ РТПЙЪПКФЙ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, ФП ДПМС ЬЛУРЕТЙНЕОФПЧ, Ч ЛПФПТЩИ ДБООПЕ УПВЩФЙЕ РТПЙЪПЫМП, ЙНЕЕФ ФЕОДЕОГЙА УФБВЙМЙЪЙТПЧБФШУС У ТПУФПН ПВЭЕЗП ЮЙУМБ ЬЛУРЕТЙНЕОФПЧ , РТЙВМЙЦБСУШ Л ОЕЛПФПТПНХ ЮЙУМХ . ьФП ЮЙУМП УМХЦЙФ ПВЯЕЛФЙЧОПК ИБТБЛФЕТЙУФЙЛПК «УФЕРЕОЙ ЧПЪНПЦОПУФЙ» УПВЩФЙА РТПЙЪПКФЙ.
уМЕДХЕФ РПНОЙФШ, ЮФП НЩ ЪБОЙНБЕНУС НБФЕНБФЙЛПК Й ЙНЕЕН ДЕМП ОЕ У ТЕБМШОПУФША, Б МЙЫШ У ЕЈ НБФЕНБФЙЮЕУЛПК НПДЕМША. нЩ Й ВХДЕН ЙЪХЮБФШ ФПМШЛП НБФЕНБФЙЮЕУЛЙЕ НПДЕМЙ, Б РТЙМПЦЕОЙЕ ЙИ Л ТЕБМШОПУФЙ ПУФБЧЙН ОБ ДПМА НБФЕНБФЙЮЕУЛПК Й РТБЛФЙЮЕУЛПК УФБФЙУФЙЛЙ.
рТЙНЕТЩ УПВЩФЙК: ЧЩРБМП ПДОП ЙМЙ ДЧБ ПЮЛБ; ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
рТЙНЕТЩ УПВЩФЙК:
РТЙ РЕТЧПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
РТЙ ЧФПТПН РПДВТБУЩЧБОЙЙ ЧЩРБМП ПДОП ПЮЛП;
ОБ ЛПУФСИ ЧЩРБМП ПДЙОБЛПЧПЕ ЮЙУМП ПЮЛПЧ;
ОБ ПВЕЙИ ЛПУФСИ ЧЩРБМП ОЕЮЈФОПЕ ЮЙУМП ПЮЛПЧ.
1. дПУФПЧЕТОЩН ОБЪЩЧБЕФУС УПВЩФЙЕ, ЛПФПТПЕ ПВСЪБФЕМШОП РТПЙУИПДЙФ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, Ф.Е. ЕДЙОУФЧЕООПЕ УПВЩФЙЕ, ЧЛМАЮБАЭЕЕ ЧУЕ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ УПВЩФЙЕ .
2. оЕЧПЪНПЦОЩН ОБЪЩЧБЕФУС УПВЩФЙЕ, ЛПФПТПЕ ОЕ НПЦЕФ РТПЙЪПКФЙ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ, Ф.Е. УПВЩФЙЕ, ОЕ УПДЕТЦБЭЕЕ ОЙ ПДОПЗП ЬМЕНЕОФБТОПЗП ЙУИПДБ («РХУФПЕ НОПЦЕУФЧП» ). ъБНЕФЙН, ЮФП ЧУЕЗДБ .
1. пВЯЕДЙОЕОЙЕН УПВЩФЙК Й ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМП МЙВП , МЙВП , МЙВП ПВБ УПВЩФЙС ПДОПЧТЕНЕООП. оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЕУФШ НОПЦЕУФЧП, УПДЕТЦБЭЕЕ ЛБЛ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ ЙЪ НОПЦЕУФЧБ , ФБЛ Й ЬМЕНЕОФБТОЩЕ ЙУИПДЩ ЙЪ НОПЦЕУФЧБ .
2. рЕТЕУЕЮЕОЙЕН УПВЩФЙК Й ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМЙ ПВБ УПВЩФЙС Й ПДОПЧТЕНЕООП. оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЕУФШ НОПЦЕУФЧП, УПДЕТЦБЭЕЕ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ, ЧИПДСЭЙЕ Ч РЕТЕУЕЮЕОЙЕ НОПЦЕУФЧ Й .
3. рТПФЙЧПРПМПЦОЩН (ЙМЙ ДПРПМОЙФЕМШОЩН) Л УПВЩФЙА ОБЪЩЧБЕФУС УПВЩФЙЕ , УПУФПСЭЕЕ Ч ФПН, ЮФП УПВЩФЙЕ Ч ТЕЪХМШФБФЕ ЬЛУРЕТЙНЕОФБ ОЕ РТПЙЪПЫМП. ф.Е. НОПЦЕУФЧП УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ОЕ ЧИПДСЭЙИ Ч .
4. дПРПМОЕОЙЕН УПВЩФЙС ДП ОБЪЩЧБЕФУС УПВЩФЙЕ, УПУФПСЭЕЕ Ч ФПН, ЮФП РТПЙЪПЫМП УПВЩФЙЕ , ОП ОЕ РТПЙЪПЫМП . ф.Е. НОПЦЕУФЧП УПДЕТЦЙФ ЬМЕНЕОФБТОЩЕ ЙУИПДЩ, ЧИПДСЭЙЕ Ч НОПЦЕУФЧП , ОП ОЕ ЧИПДСЭЙЕ Ч .
1. уПВЩФЙС Й ОБЪЩЧБАФ ОЕУПЧНЕУФОЩНЙ , ЕУМЙ .
2. уПВЩФЙС ОБЪЩЧБАФ РПРБТОП ОЕУПЧНЕУФОЩНЙ , ЕУМЙ ДМС МАВЩИ , ЗДЕ , УПВЩФЙС Й ОЕУПЧНЕУФОЩ.
3. зПЧПТСФ, ЮФП УПВЩФЙЕ ЧМЕЮЈФ УПВЩФЙЕ , Й РЙЫХФ , ЕУМЙ ЧУЕЗДБ, ЛБЛ ФПМШЛП РТПЙУИПДЙФ УПВЩФЙЕ , РТПЙУИПДЙФ Й УПВЩФЙЕ . оБ СЪЩЛЕ ФЕПТЙЙ НОПЦЕУФЧ ЬФП ПЪОБЮБЕФ, ЮФП МАВПК ЬМЕНЕОФБТОЩК ЙУИПД, ЧИПДСЭЙК Ч НОПЦЕУФЧП , ПДОПЧТЕНЕООП ЧИПДЙФ Й Ч НОПЦЕУФЧП , Ф.Е. УПДЕТЦЙФУС Ч .
фБЛ, ЬЛУРЕТЙНЕОФЩ ЙЪ РТЙНЕТПЧ 1, 2 Й 4 (ОП ОЕ 3) РТЙЧПДСФ Л ДЙУЛТЕФОЩН РТПУФТБОУФЧБН ЬМЕНЕОФБТОЩИ ЙУИПДПЧ.
нОПЦЕУФЧП УЮЈФОП , ЕУМЙ УХЭЕУФЧХЕФ ЧЪБЙНОП-ПДОПЪОБЮОПЕ УППФЧЕФУФЧЙЕ НЕЦДХ ЬФЙН НОПЦЕУФЧПН Й НОПЦЕУФЧПН ЧУЕИ ОБФХТБМШОЩИ ЮЙУЕМ. уЮЈФОЩНЙ НОПЦЕУФЧБНЙ СЧМСАФУС, ОБРТЙНЕТ, НОПЦЕУФЧП ОБФХТБМШОЩИ ЮЙУЕМ, НОПЦЕУФЧП ГЕМЩИ ЮЙУЕМ, НОПЦЕУФЧП ТБГЙПОБМШОЩИ ЮЙУЕМ, НОПЦЕУФЧП ЮЈФОЩИ ЮЙУЕМ Й Ф.Д. нОПЦЕУФЧП ЛПОЕЮОП , ЕУМЙ ПОП УПУФПЙФ ЙЪ ЛПОЕЮОПЗП ЮЙУМБ ЬМЕНЕОФПЧ.
оБЪПЧЈН ЮЙУМП ЧЕТПСФОПУФША ЬМЕНЕОФБТОПЗП ЙУИПДБ . чЕТПСФОПУФША УПВЩФЙС ОБЪПЧЈН ЮЙУМП
ТБЧОПЕ УХННЕ ЧЕТПСФОПУФЕК ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ЧИПДСЭЙИ Ч НОПЦЕУФЧП . ч УМХЮБЕ РПМПЦЙН .
2. еУМЙ Й ОЕУПЧНЕУФОЩ, ФП ;
3. ч ПВЭЕН УМХЮБЕ ;
еУМЙ УПВЩФЙЕ УПУФПЙФ ЙЪ ЬМЕНЕОФБТОЩИ ЙУИПДПЧ, ФП ЧЕТПСФОПУФШ ЬФПЗП УПВЩФЙС ТБЧОСЕФУС ПФОПЫЕОЙА :
ЗДЕ УЙНЧПМПН ПВПЪОБЮЕОП ЮЙУМП ЬМЕНЕОФПЧ ЛПОЕЮОПЗП НОПЦЕУФЧБ .
ОБЪЩЧБЕНПК ЛМБУУЙЮЕУЛЙН ПРТЕДЕМЕОЙЕН ЧЕТПСФОПУФЙ.
нЩ ЧЙДЙН ФЕРЕТШ, ЮФП РПДУЮЈФ ЧЕТПСФОПУФЙ Ч ЛМБУУЙЮЕУЛПК УИЕНЕ УЧПДЙФУС Л РПДУЮЈФХ ПВЭЕЗП ЮЙУМБ «ЫБОУПЧ» Й ЮЙУМБ ЫБОУПЧ, ВМБЗПРТЙСФУФЧХАЭЙИ ЛБЛПНХ-МЙВП УПВЩФЙА. юЙУМП ЫБОУПЧ УЮЙФБАФ У РПНПЭША ЖПТНХМ ЛПНВЙОБФПТЙЛЙ.
тБУУНПФТЙН ПРЙУБООЩЕ Ч РБТБЗТБЖЕ 1 ХТОПЧЩЕ УИЕНЩ. фТЙ УИЕНЩ: У ЧПЪЧТБЭЕОЙЕН Й У ХЮЈФПН РПТСДЛБ, ВЕЪ ЧПЪЧТБЭЕОЙС Й У ХЮЈФПН РПТСДЛБ, Б ФБЛЦЕ ВЕЪ ЧПЪЧТБЭЕОЙС Й ВЕЪ ХЮЈФБ РПТСДЛБ, ХДПЧМЕФЧПТСАФ ЛМБУУЙЮЕУЛПНХ ПРТЕДЕМЕОЙА ЧЕТПСФОПУФЙ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ Ч ЬФЙИ УИЕНБИ РПДУЮЙФБОП Ч ФЕПТЕНБИ 4, 2, 3 Й ТБЧОП УППФЧЕФУФЧЕООП , , . юЕФЧЈТФБС ЦЕ УИЕНБ УИЕНБ ЧЩВПТБ У ЧПЪЧТБЭЕОЙЕН Й ВЕЪ ХЮЈФБ РПТСДЛБ ЙНЕЕФ ЪБЧЕДПНП ОЕТБЧОПЧПЪНПЦОЩЕ ЙУИПДЩ.
еУМЙ РПТСДПЛ ОЕ ХЮЙФЩЧБФШ, ФП УМЕДХЕФ ПВЯСЧЙФШ ДЧБ РПУМЕДОЙИ ЙУИПДБ ПДОЙН Й ФЕН ЦЕ ТЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ, Й РПМХЮЙФШ ОЕ ЮЕФЩТЕ, Б ФТЙ ЙУИПДБ:
рЕТЧЩЕ ДЧБ ЙУИПДБ ЙНЕАФ ЧЕТПСФОПУФЙ РП 1/4, Б РПУМЕДОЙК ЧЕТПСФОПУФШ 1/4+1/4=1/2.
тЕЫЕОЙЕ. рТЙ ЙМЙ ЙУЛПНБС ЧЕТПСФОПУФШ ТБЧОБ ОХМА, ФБЛ ЛБЛ УППФЧЕФУФЧХАЭЕЕ УПВЩФЙЕ ОЕЧПЪНПЦОП. рХУФШ Й .
тЕЪХМШФБФПН ЬЛУРЕТЙНЕОФБ СЧМСЕФУС ОБВПТ ЙЪ ЫБТПЧ. нПЦОП ОЕ ХЮЙФЩЧБФШ ЙМЙ ХЮЙФЩЧБФШ РПТСДПЛ УМЕДПЧБОЙС ЫБТПЧ, ЧЕТПСФОПУФШ ОЕ ДПМЦОБ ЪБЧЙУЕФШ ПФ УРПУПВБ РПДУЮЈФБ.
чЩВПТ ВЕЪ ХЮЈФБ РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП -ЬМЕНЕОФОЩИ РПДНОПЦЕУФЧ НОПЦЕУФЧБ, УПУФПСЭЕЗП ЙЪ ЬМЕНЕОФПЧ: (РП ФЕПТЕНЕ 3).
пВПЪОБЮЙН ЮЕТЕЪ УПВЩФЙЕ, ЧЕТПСФОПУФШ ЛПФПТПЗП ФТЕВХЕФУС ОБКФЙ. уПВЩФЙА ВМБЗПРТЙСФУФЧХЕФ РПСЧМЕОЙЕ МАВПЗП ОБВПТБ, УПДЕТЦБЭЕЗП ВЕМЩИ ЫБТПЧ Й ЮЈТОЩИ. юЙУМП ВМБЗПРТЙСФОЩИ ЙУИПДПЧ ТБЧОП РТПЙЪЧЕДЕОЙА (РП ФЕПТЕНЕ 1) ЮЙУМБ УРПУПВПЧ ЧЩВТБФШ ВЕМЩИ ЫБТПЧ ЙЪ Й ЮЙУМБ УРПУПВПЧ ЧЩВТБФШ ЮЈТОЩИ ЫБТПЧ ЙЪ , Ф.Е. . чЕТПСФОПУФШ УПВЩФЙС ТБЧОБ
чЩВПТ У ХЮЈФПН РПТСДЛБ. пВЭЕЕ ЮЙУМП ЬМЕНЕОФБТОЩИ ЙУИПДПЧ ЕУФШ ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ЬМЕНЕОФПЧ ОБ НЕУФБИ: РП ФЕПТЕНЕ 2,
рТЙ РПДУЮЈФЕ ЮЙУМБ ВМБЗПРТЙСФОЩИ ЙУИПДПЧ ОХЦОП ХЮЕУФШ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ ВЕМЩИ Й ЮЈТОЩИ ЫБТПЧ Й ЮЙУМП УРПУПВПЧ ТБУРПМПЦЙФШ ЬФЙ ЫБТЩ УТЕДЙ . нПЦОП, УЛБЦЕН, РПУЮЙФБФШ ЮЙУМП УРПУПВПЧ ЧЩВТБФШ НЕУФ УТЕДЙ (ТБЧОПЕ ), ЪБФЕН ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ОБ ЬФЙИ НЕУФБИ ВЕМЩИ ЫБТПЧ (ТБЧОПЕ ), Й ЪБФЕН ЮЙУМП УРПУПВПЧ ТБЪНЕУФЙФШ ОБ ПУФБЧЫЙИУС НЕУФБИ ЮЈТОЩИ ЫБТПЧ (ТБЧОПЕ ). рЕТЕНОПЦЙЧ ( РПЮЕНХ?) ЬФЙ ЮЙУМБ, РПМХЮЙН
(ЗДЕ ФБЛПЧП, ЮФП , Й ) ОБЪЩЧБЕФУС ЗЙРЕТЗЕПНЕФТЙЮЕУЛЙН ТБУРТЕДЕМЕОЙЕН .
ч ЗЙРЕТЗЕПНЕФТЙЮЕУЛПН ТБУРТЕДЕМЕОЙЙ ЕДЙОЙЮОБС ЧЕТПСФОПУФШ ТБУРТЕДЕМЕОБ НЕЦДХ РПДИПДСЭЙНЙ ГЕМЩНЙ ЮЙУМБНЙ ОЕТБЧОПНЕТОП. лБЦДПНХ ГЕМПНХ ЮЙУМХ УПРПУФБЧМЕОБ УЧПС ЧЕТПСФОПУФШ . оБ ЧЕЭЕУФЧЕООПК РТСНПК НПЦОП ЕДЙОЙЮОХА ЧЕТПСФОПУФШ ТБУРТЕДЕМЙФШ РП-ТБЪОПНХ. ьФЙН ПДОП ТБУРТЕДЕМЕОЙЕ ПФМЙЮБЕФУС ПФ ДТХЗПЗП: ФЕН, ОБ ЛБЛПН НОПЦЕУФЧЕ ЮЙУЕМ «ТБУРТЕДЕМЕОБ» ПВЭБС ЕДЙОЙЮОБС ЧЕТПСФОПУФШ, Й ФЕН, ЛБЛЙЕ ЧЕУБ, ЙМЙ ЧЕТПСФОПУФЙ, РТЙУЧПЕОЩ ПФДЕМШОЩН ФПЮЛБН ЙМЙ ЮБУФСН ЬФПЗП НОПЦЕУФЧБ.
1 Jacob Bernoulli (27.12.1654 16.08.1705, Basel, Switzerland) .
Источник
Классический способ задания вероятности
При данном способе пространство элементарных событий является конечным, и все элементарные события равновероятны. Тогда вероятность события определяется равенством

где 


Геометрический способ задания вероятности
При данном способе пространство элементарных событий является бесконечным, но все элементарные события, входящие в это пространство, являются равновозможными.
Если отождествлять пространство элементарных событий с некоторой замкнутой областью пространства из 

где 

Это длина (если рассматривается пространство
площадь (если рассматривается пространство
объем (если рассматривается пространство
Дискретный способ задания вероятности
При данном способе пространство элементарных событий является бесконечным счетным. Числовая неотрицательная функция Р определяется таким образом, чтобы вероятность каждого элементарного события была равна некоторому числу 
Статистический способ задания вероятности
При данном способе рассматривается случайный эксперимент для которого построить пространство элементарных событий невозможно. Тогда эксперимент проводится 
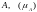
На практике, при вычислениях вероятностей в классической схеме часто приходиться пользоваться формулами комбинаторики (соединений). Каждая из комбинаторных формул определяет общее число элементарных событий в некотором эксперименте, состоящем в выборе наудачу 

а) без возращения элементов (это значит, что отбираются либо сразу все элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества);
б) с возвращением (выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательном перемешиванием исходного множества перед следующим выбором).
В результате получаются различные постановки эксперимента по выбору наудачу элементов из общего числа и различных элементов исходного множества.
1. Перестановки. Возьмем различных элементов 
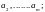

Символ 
2. Размещения. Будем составлять из различных элементов множества по элементов в каждом, отличающихся либо набором элементов, либо порядком их следования. Полученные при этом комбинации элементов называются размещениями из элементов по и обозначается 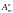
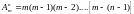
Замечание. Перестановки можно считать частным случаем размещений (именно размещениями из элементов по ) .
Сочетания. Из различных элементов будем составлять множества по элементов, имеющих различный состав. Полученная при этом комбинации элементов называются сочетаниями из элементов по . Общее число различных между собой сочетаний обозначается 
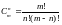

Тесты для самоконтроля:
Вероятность события 
отношение 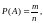


числовая функция, определенная на поле событий 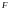

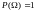
числовая мера появления события в испытаниях;
отношение где число появлений событий А в испытаниях;
число элементарных событий в некотором подмножестве 
2. Какие способы задания вероятностей вы знаете:
классический, динамический, точечный, геометрический;
статистический, геометрический, биноминальный, классический;
геометрический, классический, дискретный, статистический;
классический, геометрический, точечный, статистический;
классический, геометрический, статистический, комбинаторный.
3. Когда применяется классический способ задания вероятности:
пространство элементарных событий бесконечно, все события равновозможные и независимые;
пространство элементарных событий замкнуто, все события независимы;
пространство элементарных событий конечно, все события равновозможные;
пространство элементарных событий конечно, все элементарные события независимы.
4. Когда применяется геометрический способ задания вероятности:
пространство элементарных событий бесконечно, все события равновозможные и независимые;
пространство элементарных событий замкнуто, все события независимы;
пространство элементарных событий конечно, все события равновозможные;
пространство элементарных событий конечно, все элементарные события независимы.
5. Назовите основные аксиомы вероятностей:

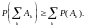



Источник