Коэн кун способ настройки

ПИД-регулятор. Методика настройки

2020-07-10 Промышленное 12 комментариев

ПИД-регулятор (пропорционально-интегрально-дифференциальный) — устройство, с обратной связью, применяемое в автоматических системах управления для поддержания заданного значения параметра. Благодаря своей универсальности они широко применяются в различных технологических процессах.

Выходной сигнал регулятора определяется по следующей формуле:

u (t) = P + I + D = Kp e (t) + Ki ∫e (t) dt + Kd de (t)/dt

u (t) – выходной сигнал регулятора;

P – пропорциональная составляющая;

I – интегрирующая составляющая;

D – дифференцирующая составляющая;

Kp — пропорциональный коэффициент

Ki — интегральный коэффициент

Kd – дифференциальный коэффициент

e (t) – ошибка рассогласования

Задачи ПИД-регулятора в системах АСУ ТП

Основная задача ПИД регулятора состоит в поддержании определенного значения параметра технологического процесса на заданном уровне. То есть говоря простым языком, задача ПИД-регулятора заключается в том, чтобы учитывая полученные значения с датчиков (обратная связь) воздействовать на объект управления, плавно подводя регулируемое значение к заданным уставкам. Применение ПИД регуляторов целесообразно, а зачастую и единственно возможно в процессах, где необходима высокая точность переходных процессов, непрерывный контроль и регулирование заданных параметров, недопустимы значительные колебания в системе.

Сравнение ПИД –регулятора с позиционным регулированием

В системах АСУ ТП наибольшее распространение получили два типа регуляторов – двухпозиционный и ПИД.

Двухпозиционный регулятор наиболее простой в использовании и широко распространенный.

Данный тип регулятора сравнивает значение входной величины с заданным параметром уставки. Если значение измеренной величины ниже заданного значения уставки, регулятор включает исполнительное устройство, при превышении заданного значения, исполнительное устройство выключается. Для предотвращения слишком частого срабатывания устройства, в следствии колебаний системы и следовательно изменении значений, задается минимальный и максимальный порог срабатывания — гистерезис, или по другому зона нечувствительности, мертвая зона, дифференциал. Например, нам необходимо поддерживать температуру в 15°С. Если гистерезис задан 2°, то регулятор будет включать нагрев при 14°С и отключать соответственно при 16°С.

Чем меньше значение гистерезиса, тем точнее будет процесс регулирования, но увеличивается частота срабатывания ,что в конечном итоге приводит к износу коммутационных аппаратов. Увеличение гистерезиса уменьшит частоту переключений, но при этом увеличивается амплитуда колебаний регулируемого параметра, что приведет к ухудшению точности регулирования.

Так или иначе, при таком типе регулирования происходят незатухающие колебания, частота и амплитуда которых зависит от параметров системы. Поэтому данный метод обеспечивает хороший результат в системах, обладающих инерционностью и малым запаздыванием. В частности, такой метод широко применяется при регулировании температуры в нагревательных печах.

В отличии от двухпозиционного с помощью ПИД-регулятора удается свести колебания системы к минимуму, благодаря тому, что при таком методе регулирования учитываются различные значения системы — фактическая величина, заданное значение, разность, скорость. Это позволяет стабилизировать систему и добиться повышения точности в десятки раз по сравнению с двухпозиционным методом. Конечно, здесь многое зависит от правильно подобранных коэффициентов ПИД регулятора.

Для того, чтобы правильно выбрать необходимый тип регулятора необходимо хотя бы приблизительно знать характеристики управляемого объекта , требования к точности регулирования, характер возмущений, воздействующих на объект регулирования.

Составляющие ПИД-регулятора

В стандартном ПИД-регуляторе есть три составляющие и каждая из них по своему воздействует на управление.

Пропорциональная — P (t) = Kp * e (t)

Учитывает величину рассогласования заданного значения и фактического. Чем больше отклонения значения, тем больше будет выходной сигнал, то есть пропорциональная составляющая пытается компенсировать эту разницу.

Однако пропорциональный регулятор не способен компенсировать полностью ошибку рассогласования. Всегда будет присутствовать так называемая статическая ошибка, которая равна такому отклонению регулируемой величины, которое обеспечивает выходной сигнал, стабилизирующий выходную величину именно на этом значении. При увеличении коэффициента пропорциональности Kp статическая ошибка уменьшается, но могут возникнуть автоколебания и снижение устойчивости системы.

Интегральная – I (t) = Ki ∫e (t) dt

Интегральная составляющая используется для устранения статической ошибки. Она складывает значение предыдущих ошибок рассогласования и компенсирует их, можно сказать, что учится на предыдущих ошибках. То есть ошибка рассогласования умножается на коэффициент интегрирования и прибавляется к предыдущему значению интегрирующего звена. При выходе системы на заданный режим, интегральная составляющая перестает изменяться и не оказывает какого-либо серьезного воздействия на систему. Физически интегральная составляющая представляет задержку реакции регулятора на изменение величины рассогласования, внося в систему некоторую инерционность, что может быть полезно для управления объектами c большой чувствительностью.

Дифференциальная – D (t) = Kd de (t)/dt

Дифференциальная составляющая учитывает скорость изменения регулируемой величины, противодействуя предполагаемым отклонениям, вызванными возмущениями системы или запаздыванием. И чем больше будет величина отклоняться от заданной, тем сильнее будет противодействие, оказываемое дифференциальной составляющей. То есть она предугадывает поведение системы в будущем. При достижении величины рассогласования постоянного значения дифференциальная составляющая перестает оказывать воздействие на управляющий сигнал.

На практике какая-либо из составляющих может не использоваться (чаще всего Д-дифференциальная) и тогда мы получаем П-регулятор, ПИ-регулятор.

Методика настройки ПИД-регулятора

Выбор алгоритма управления и его настройка является основной задачей в процессе проектирования и последующего удовлетворительного запуска агрегата в промышленную или иную эксплуатацию.

В основе методики лежит закон Циглера-Никольса, являющийся эмпирическим и основанным на использовании данных, полученных экспериментально на реальном объекте.

В результате ознакомления с методикой, а также при близком рассмотрении объектов регулирования, были выбраны формулы и коэффициенты ближе всего подходящие к реальному объекту регулирования.

Объект регулирования – камерная электрическая печь. Число зон регулирования от 24 до 40. Каждая зона есть набор электронагревателей. Материал нагревателей нихром. Тип — проволочные, навитые на керамические трубки.

Требования: поддержание температуры по зонам печи +/- 5С.

МЕТОДИКА:

Настройка пропорциональной компоненты (Xp)

1. Перед настройкой зоны пропорциональности интегральная и дифференциальная компоненты отключаются:

• Постоянная интегрирования устанавливается минимально возможной (Ти =0),
• Постоянная дифференцирования минимально возможной (Тд = 0).

Тο — начальная температура в системе;
Тsp — заданная температура (уставка);
∆T — размах колебаний температуры;
∆t — период колебаний температуры.

1. Меняем значение пропорциональной составляющей Xp от минимума (0) до момента, пока не появятся устойчивые колебания системы с периодом ∆t.

Система должна находится в постоянном колебательном процессе, притом колебательный процесс незатухающий, где ∆T– характеристика колебания равная значению величины рассогласования (±10С, или как по заданию). Колебания должны быть одинаковы от Тsp.

После получения данной кривой на нашем объекте, засекаем время периода колебаний ʌt – полный период. Данное время есть характеристика системы, оборудования.

3. Используя полученные параметры рассчитываем Ти и Тд.

Зона пропорциональности	Коэффициент передачи	Постоянная времени интегрирования	Постоянная времени дифференцирования
П-регулятор	2*PBs	0.5*Xp
ПИ-регулятор	2.2*PBs	0.45*Xp	0.83*ʌТ
ПИД-регулятор	1.67*PBs	0.6*Xp	0.5*ʌТ	0.125*ʌТ

Цифры в формулах для расчета коэффициентов ПИД-регулирования скорректированы на основе запуска камерной электрической печи в опытно-промышленную эксплуатацию. И конечно в зависимости от типа объекта регулирования могут незначительно меняться.

Вывод

Благодаря достаточно высоким получаемым результатам ПИД-регуляторы нашли широкое применение в системах автоматического управления.

При этом важно подчеркнуть, что настройка ПИД-регулятора является процессом довольно трудоемким и требует определенных знаний и индивидуального подхода для различных объектов управления.

Источник

Простой метод настройки ПИД регулятора

Есть два похода к настройке ПИД регулятора. Первый – синтез регулятора, то есть вычисление параметров регулятора на основании модели системы. Данный метод позволяет очень точно рассчитать параметры регулятора, но он требует основательного погружения в ТАУ.

Второй метод – ручной подбор параметров (коэффициентов). Это метод научного тыка проб и ошибок. Берем готовую систему, меняем один (или сразу несколько коэффициентов) регулятора, включаем регулятор и смотрим за работой системы. В зависимости от того, как ведет себя система с выбранными коэффициентами (недо/пере регулирование) опять меняем коэффициенты и повторяем эксперимент. И т. д. Ну, такой метод имеет право на жизнь, главное представлять как изменение того или иного коэффициента повлияет на систему (что бы не действовать совсем наугад).

Есть более «оптимизированный» метод подбора коэффициентов – метод Зиглера–Никольса.

Сразу скажу, что метод работает не для любой системы, результаты получаются не самыми оптимальными. Но, зато, метод очень простой и годится для базовой настройки регулятора в большинстве систем.

Суть метода состоит в следующем:

1. Выставляем все коэффициенты (Kp, Ki, Kd) в 0.
2. Начинаем постепенно увеличивать значение Kp и следим за реакцией системы. Нам нужно добиться, чтобы в системе начались устойчивые колебания (вызванные перерегулированием). Увеличиваем Kp, пока колебания системы не стабилизируются (перестанут затухать).
3. Запоминаем текущее значение Kp (обозначим его Ku) и замеряем период колебаний системы (Tu).

Все. Теперь используем полученные значения Ku и Tu для расчета всех параметров ПИД регулятора по формулам:

Kp = 0.6 * Ku
Ki = 2 * Kp / Tu
Kd = Kp * Tu / 8

Готово. Для дискретных регуляторов нужно еще учесть период дискретизации – T ( умножить на Ki та Т, разделить Kd на Т).

Еще раз повторюсь, ТАУ изучать нужно, синтез регуляторов рулит, описанный метод годится для базовой настройки, подходит не для всех систем и т. д. Но данный метод очень простой, и вполне годится для «бытового» уровня.

Источник

Исследование методов настройки ПИД-регулятора для систем с малыми постоянными времени

Рубрика: 3. Автоматика и вычислительная техника

Дата публикации: 29.05.2019

Статья просмотрена: 809 раз

Библиографическое описание:

Гусаров, А. В. Исследование методов настройки ПИД-регулятора для систем с малыми постоянными времени / А. В. Гусаров, П. С. Кошляков. — Текст : непосредственный // Технические науки в России и за рубежом : материалы VIII Междунар. науч. конф. (г. Краснодар, июнь 2019 г.). — Краснодар : Новация, 2019. — С. 22-23. — URL: https://moluch.ru/conf/tech/archive/332/15126/ (дата обращения: 18.11.2021).

В работе описывается исследование системы регулирования скорости вращения асинхронного двигателя. Данная тема является актуальной в связи с тем, что в настоящее время настройка параметров системы регулирования скорости вращения асинхронного двигателя является сложной задачей, требующей больших затрат времени на подбор коэффициентов.

Ключевые слова: ПИД-регулятор, асинхронный двигатель, автоподбор коэффициентов.

ПИД-регуляторы находят широкое применение в современных системах автоматического регулирования, таких как управление термосистемами и системами позиционирования. Использование ПИД-регуляторов помогает уменьшить энергетические потери на настройку системы и обеспечивают более быстрый выход на требуемые параметры.

Для корректной работы регулятора необходимо правильно подобрать его коэффициенты. От правильности подбора коэффициентов будет зависеть точность и скорость работы системы. Довольно часто эмпирический подбор коэффициентов не приносит желаемых результатов и занимает много времени. В связи с этим возникает необходимость в использовании математических методов настройки регулятора. Существует несколько таких методов, но в данной работе будут рассмотрены самые распространённые: метод Зиглера-Никольса, метод CHR и метод Коэна-Куна.

Зиглер и Никольс предложили два метода настройки ПИД‑регуляторов [1]. Один из них основан на параметрах отклика объекта на единичный скачок, второй — на частотных характеристиках объекта управления.

В отличие от Зиглера и Никольса, которые использовали в качестве критерия качества настройки декремент затухания, равный 4, Chien, Hrones и Reswick (CHR) [2] использовали критерий максимальной скорости нарастания при отсутствии перерегулирования или при наличии не более чем 20‑процентного перерегулирования. Такой критерий позволяет получить больший запас устойчивости, чем в методе Зиглера‑Никольса.

Метод CHR даёт две разные системы параметров регулятора. Одна из них получена при наблюдении отклика на изменение уставки (таблица 1.2), вторая — при наблюдении отклика на внешние возмущения (таблица 1.3). Какую систему параметров выбирать, зависит от того, что важнее для конкретного регулятора: качество регулирования при изменении уставки или ослабление внешних воздействий. Если же важно и то и другое, то необходимо использовать регуляторы с двумя степенями свободы.

Метод CHR использует аппроксимацию объекта моделью первого порядка с задержкой.

Правила настройки Коэна-Куна хорошо работают практически во всех саморегулирующихся процессах. Эти правила первоначально были разработаны для быстрого реагирования, но это приводит к колебаниям с большим перерегулированием. При небольшой модификации правил настройки Коэна-Куна контуры управления могут реагировать быстро, но они гораздо менее подвержены колебаниям [3].

Рассматриваемые методы, в основном, используются для систем с большой инерцией. Они хорошо работают с системами, в которых время регулирования занимает продолжительное время (единицы, десятки секунд и более). В связи с этим возникает необходимость проверить актуальность рассматриваемых методов для малоинерционной системы с малыми постоянными времени.

Для исследования методов настройки ПИД-регуляторов был разработан стенд, включающий в себя асинхронный двигатель, который вращает вентилятор с заслонкой на выходном патрубке вентилятора, датчик положения заслонки и имитатор изменения давления на заслонку, регулирующую поток воздуха от вентилятора. Реализация автоматического регулирования мощностью потока воздуха выполнена на основе ПИД-регулятора.

ПИД-регулятор формирует управляющий сигнал, являющийся суммой трёх слагаемых, первое из которых пропорционально разности входного сигнала и сигнала обратной связи (сигнал рассогласования), второе — интеграл сигнала рассогласования, третье — производная сигнала рассогласования.

В разработанном лабораторном стенде существует возможность использования двух вариантов реализаций ПИД-регулирования: рекуррентная и дискретная. Используя данные, полученные в ходе проведения эксперимента, были выбраны основные методы для расчёта коэффициентов регулятора.

При использовании программной реализации метода автоматического регулирования часто переходят к рекуррентной реализации регулятора. Особенностью рекуррентной реализации является использования ошибки рассогласования за текущий шаг и за два предыдущих:

(1)

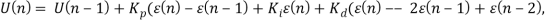
где  — ошибка рассогласования; K_p, K_i, K_d — пропорциональный, интегральный и дифференциальный коэффициенты.

Ошибка рассогласования рассчитывается по формуле

где y_i – выходное значение регулятора; y_зад — заданное входное значение (уставка).

В дискретной реализации метода расчёта выходного сигнала используется формула

(3)

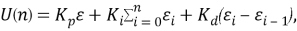
где  — ошибка рассогласования; K_p, K_i, K_d — пропорциональный, интегральный и дифференциальный коэффициенты.

Ошибка рассогласования рассчитывается по формуле (2).

В ходе проведённых экспериментов было определено, что метод Коэна-Куна не подходит для малоинерционных систем. С коэффициентами, полученными в результате расчёта методом Коэна-Куна, система ведёт себя нестабильно.

Методы CHR и Зиглера-Никольса являются актуальными для малоинерционных систем. Наиболее хорошо в малоинерционных системах реализуется метод CHR.

Источник