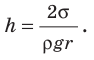- Способы определения поверхностного натяжения жидкостей
- Поверхностное натяжение жидкости — формулы и определение с примерами
- Сила поверхностного натяжения
- Коэффициент поверхностного натяжения
- Капиллярные явления
- Поверхностное натяжение жидкости
- Каковы особенности поверхностного слоя жидкости
- Что такое сила поверхностного натяжения
- Где проявляется поверхностное натяжение
- Почему одни жидкости собираются в капли, а другие растекаются
- Почему жидкость поднимается в капиллярах
- Пример решения задачи
Способы определения поверхностного натяжения жидкостей



Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя.
В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами.
Статические методы:
1. Метод поднятия в капилляре
| Основан на определении высоты столба жидкости h в капилляре радиуса r при полном смачивании; поверхностное натяжение рассчитывают по формуле: |
Высота подъема 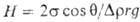
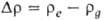
При идеальном смачивании, т. е. когда краевой угол смачивания равен нулю справедливо уравнение:

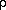
g — ускорение свободного падения.
Недостатком этого метода является зависимость высоты подъема жидкости от характера смачивания стенок капилляра исследуемой жидкостью
2. Метод Вильгельми
 | Универсальный метод, особенно подходит для измерения поверхностного натяжения в течение длительного промежутка времени. Измеряется усилие, возникающее в процессе отрыва стеклянной пластины от поверхности жидкости |
При погружении пластины с периметром сечения L в смачивающую жидкость вес пластины
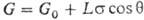
где G0— вес сухой пластины
3. Метод лежачей капли
| Метод основан на измерении формы капли, находящейся на несмачиваемой поверхности. |
4. Метод определения по форме висячей капли.
 | Измеряется возможность проводить измерения при повышенной температуре и давлении. Оптическими методами анализируют геометрию капли. |
5. Метод вращающейся капли
 | Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости. Капля жидкости плотностью r1 помещается в трубку с более тяжелой (плотность r2) жидкостью. При вращении трубки с угловой скоростью w капля вытягивается вдоль оси, принимая приближенно форму цилиндра радиуса r. Расчетное ур-ние: 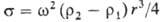 |
Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения.
Динамические методы:
1. Метод Дю Нуи (метод отрыва кольца).
 | Метод является классическим. Сущность метода вытекает из названия. Платиновое кольцо поднимают из жидкости, смачивающей его, усилие отрыва и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения ПАВ, трансформаторных масел и т. д. |
Для отрыва проволочного кольца радиусом R от пов-сти жидкости требуется сила
2. Сталагмометрический, или метод счета капель.
Метод основан на определении объема капли, вытекающей из капилляра с известным радиусом
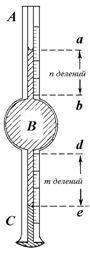 | Рис.Схема простейшего сталагмометра На рис.показана схема простейшего сталагмометра, который представляет собой сферический пузырек В известного объема Vk, ограниченный метками b и d и соединенный с двумя калиброванными капиллярами, имеющими объем каждого деления vе. Сталагмометр заполняют жидкостью, затем позволяют мениску очень медленно перемещаться по капилляру, перекрывая частично доступ воздуха в капилляр А с помощью резиновой трубки и зажима таким образом, чтобы каждая капля образовывалась за время не менее 4 с. После падения первой капли проводится отсчет деления, соответствующего верхнему мениску a в капилляре А (n делений от метки a). Скорость последующего образование капель также контролируют и устанавливают время образования капли не менее 4–5 с. После достижения мениском метки, например e в нижнем капилляре C (m делений от метки d), определяют объем одной капли при числе подсчитанных вытекших из сталагмометра капель N : 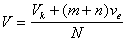 |
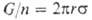
где G-общий вес n капель, оторвавшихся под действием силы тяжести от среза капиллярной трубки радиусом r. Для повышения точности правую часть умножают на поправочный коэф., зависящий от г и объема капли.
К недостаткам сталагмометрического метода можно отнести возможность испарения жидкости с поверхности капель при их длительном образовании и необходимость введения поправочных коэффициентов для точного определения поверхностного натяжения.

При учете всех поправок погрешность сталагмометрического метода не превышает 1%.
3. Метод максимального давления пузырька (метод Ребиндера).
 | Оптимально подходит для измерения величины поверхностного натяжения в зависимости от возраста поверхности. Измеряется давление, которое необходимо приложить, чтобы пузырек пробульковал из капилляра в жидкость. |
Расчет основан на ур-нии Лапласа. При выдавливании пузырька в жидкость через калиброванный капилляр радиусом г перед моментом отрыва давление
В этом случае определяется так называемое динамическое поверхностное натяжение, которое зависит от скорости пробулькавания пузырька.
4. Метод осциллирующей струи
5. Метод стоячих волн
6. Метод бегущих волн
При возмущении жидкости пластиной «лежащей» на её поверхности, по ней начинает распространяться цуг волн. Если просветить кювету с жидкостью импульсным источником света с частотой равной частоте возмущения, то на экран спроецируется «стоячая» волновая картина. Измеряя длину волны на экране и геометрически перерассчитывая её (зная расстояние от источника света до поверхности жидкости и расстояние от поверхности до экрана, а также про подобие треугольников) можно получить величину поверхностного натяжения по формуле:
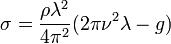
Источник
Поверхностное натяжение жидкости — формулы и определение с примерами
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
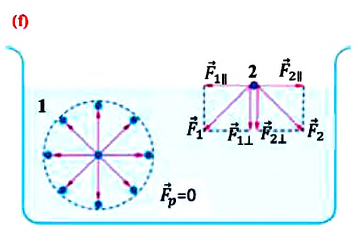
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения — это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 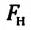
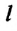
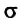
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения — численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск — это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 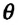
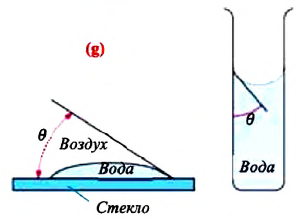
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде — смачивающая жидкость (g).
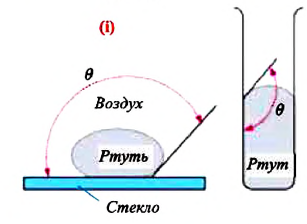
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек — капилляров.
Капилляр — это узкая трубка (канал) диаметром меньше 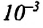
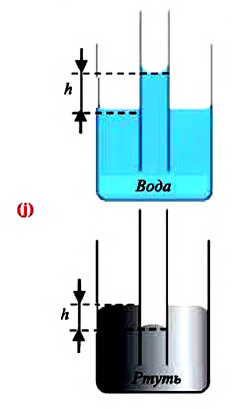
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Характеристики жидкости, поднимающейся в капилляре
Где 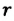
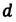
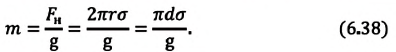
Если жидкость полностью смачиваемая, то получаем в
Где 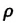
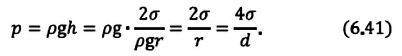
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
Каковы особенности поверхностного слоя жидкости
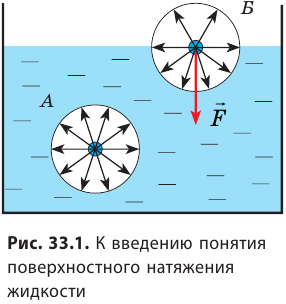
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
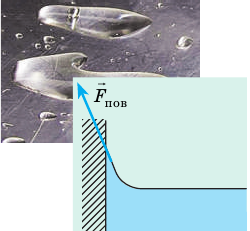
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
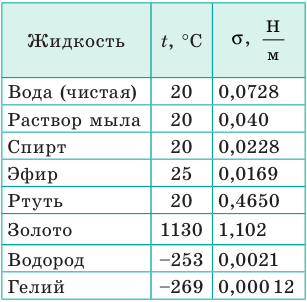
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (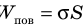
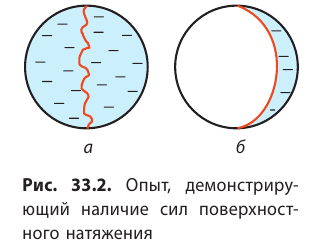
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
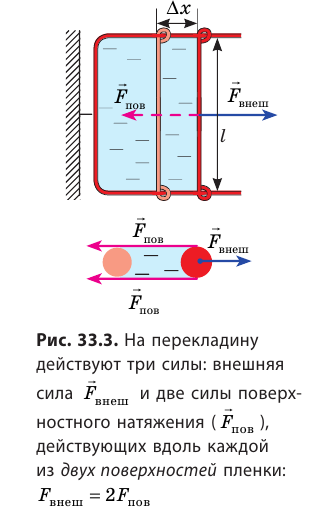
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 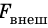
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 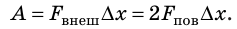
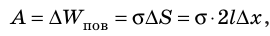
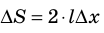
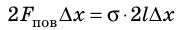
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения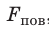
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
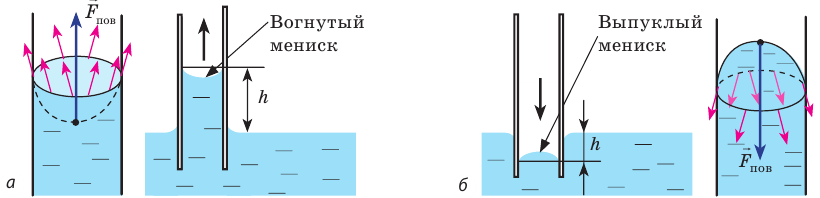
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (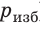
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
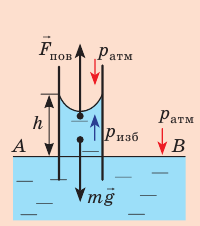
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения ( 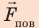
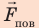
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 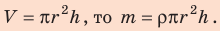
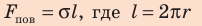
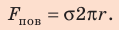
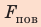

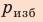
где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
- Высота подъема жидкости в капилляре прямо пропорциональна поверхностному натяжению жидкости и обратно пропорциональна плотности жидкости и радиусу капилляра:
.
- Лапласово давление (избыточное давление) под сферической поверхностью жидкости прямо пропорционально поверхностному натяжению жидкости и обратно пропорционально радиусу кривизны мениска:
.
- Молекулы поверхностного слоя жидкости обладают избыточной потенциальной энергией по сравнению с молекулами, находящимися внутри жидкости; эту энергию называют поверхностной энергией.
- Физическая величина, которая характеризует жидкость и равна отношению поверхностной энергии к площади поверхности жидкости, называется поверхностным натяжением жидкости:
. Поверхностное натяжение также равно силе, которая действует на единицу длины линии, ограничивающей поверхность жидкости:
.
- Под искривленной поверхностью жидкости возникает избыточное (отрицательное или положительное) давление, благодаря которому жидкость поднимается в капиллярах, которые смачивает, и опускается в капиллярах, которые не смачивает. Высота подъема (опускания) жидкости в капилляре:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник




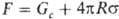
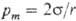
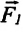


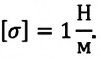
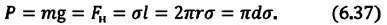
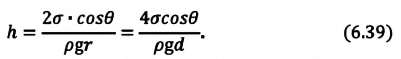
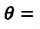
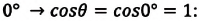


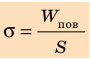
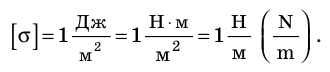
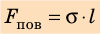
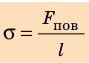



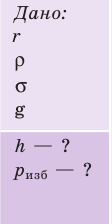
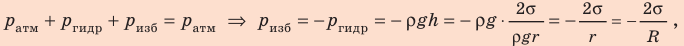
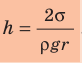 .
.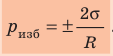 .
.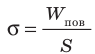 . Поверхностное натяжение также равно силе, которая действует на единицу длины линии, ограничивающей поверхность жидкости:
. Поверхностное натяжение также равно силе, которая действует на единицу длины линии, ограничивающей поверхность жидкости: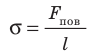 .
.