Коэффициент эластичности способы расчета

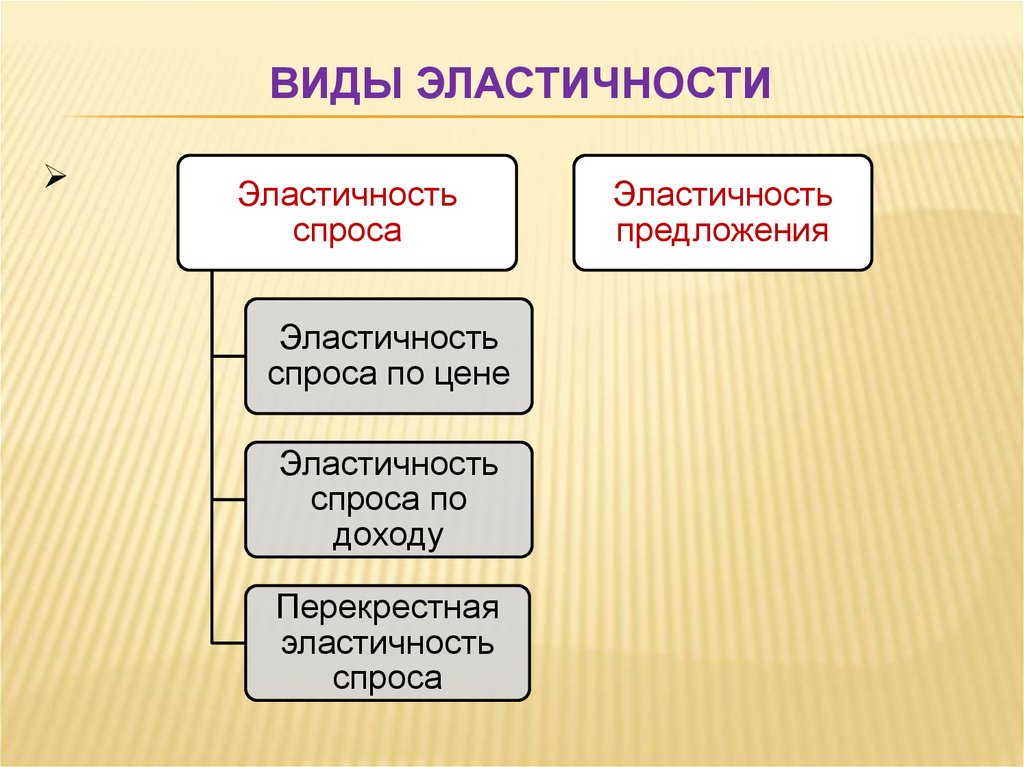
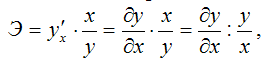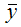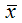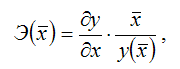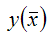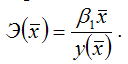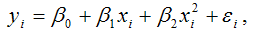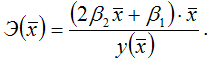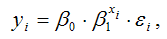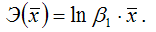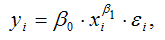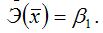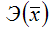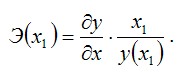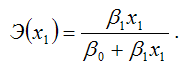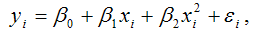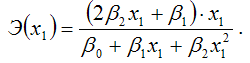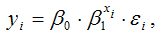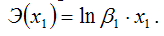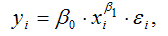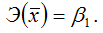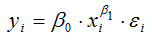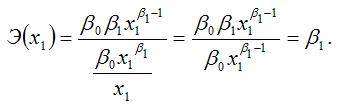Формула коэффициента эластичности

Понятие эластичности

Соотношения спроса и предложения в экономической теории отражается посредством многих факторов. С этим же связано и понятие эластичности. Эластичность бывает двух видов:

Формула коэффициента эластичности чаще всего используется для контроля реакции покупателей на изменения цен на продукцию (снижение или рост).

Формула коэффициента эластичности спроса по цене

Степень чувствительности потребителя к изменению в цене можно измерять с помощью показателя эластичности спро­са по цене.

Коэффициент эластичности спроса по цене вычисляется отношением количества запрашиваемой продукции к изменению цен, вызвавшего данное изменение спроса (определяется в процентах).

Формула коэффициента эластичности спроса по цене представлена в следующем виде:

Е = ∆Q / ∆P (%)

Процентные изменения объемов предложения и спроса вычисляются при помощи соответствующих формул:

∆Q(%) = (Q2-Q1)/Q1

∆P(%) = (P2-P1)/P1

Здесь Q1 – начальный объем спроса,

Q2 — текущий спрос;

Р1 — начальная цена,

Р2 – настоящая цена.

При использовании данных вычислений коэффициента эластичности в общем примет следующий вид:

Е = (Q2-Q1)/Q1 (%) :(P2-P1)/P1 (%)

Или Е = (Q2-Q1)P1 / (P2-P1)Q1

Формула коэффициента эластичности предложения

Формула коэффициента эластичности предложения по цене рассчитывается по аналогии с формулой коэффициента эластичности спроса по цене. Отличие заключается в том, что вместо величины спроса берем величину предложения:

Es = (Q2-Q1)/(Q2 + Q1) ^ (P2-P1)/(P2+P1)

Из формулыможно сделать вывод, что абсолютно неэластичное предложение графически отражается вертикальной прямой графика предложения, а абсолютно эластичное предложение отражается горизонтальной линией.

На эластичность предложения могут оказывать влияние следующие факторы:

• Издержки компании,
• Степень загрузки производственных мощностей,
• Наличие свободной рабочей силы,
• Резервы производства и др.

Анализ эластичности

Выделяют три значения показателя эластичности:

• Больше одного (Е D _Р> 1), при этом спрос (предложение) можно определить как эластичный (чем больше показатель, тем спрос эластичнее).
• Меньше единицы (Е D _Р ПРИМЕР 1

Задание	Вычислить показатель эластичности спроса по цене, если известно, что цена выросла на 5%, а спрос при этом уменьшился на 2%. Какой вид эластичности характерен для данной ситуации?
Решение	Формула эластичности спроса по цене для решения данной задачи выглядит так:

Е = ∆Q / ∆P (%)

Вывод. Мы видим, что значение эластичности меньше единицы, поэтому спрос можно определить как неэластичный. Отрицательное значение показателя не принимается во внимание, так как показатель определяется по модулю.

Ответ Е = — 0,4, спрос неэластичный

Задание	Рассчитать коэффициент эластичности предложения, если цена продукции составляет 85 рублей, при этом предложение – 200 штук. При росте цены до 105 рублей, предложение увеличилось на 100 штук.
Решение	Простыми расчетами мы определим, что во втором случае предложение составит 300 штук.

Формула коэффициента эластичности предложения по цене для данной задачи:

Es = (Q2-Q1)/(Q2 + Q1) ^ (P2-P1)/(P2+P1)

Es = (300-200)/(300+200) ^ (105 – 85)/(105+85) = 100/500 : 20/190 = 1,9

Вывод. Мы видим, что эластичность предложения больше единицы, что говорит о том, что предложение эластично.

Источник

Методы подсчета коэффициента эластичности

При подсчете коэффициента эластичности используют два основных метода:

Эластичность по дуге (дуговая эластичность) — применяется при измерении эластичности между двумя точками на кривой спроса или предложения и предполагает знание первоначальных и последующих уровней цен и объемов.

· — начальная цена

· — новая цена

· — первоначальный объем

· — новый объем

Использование формулы дуговой эластичности дает лишь приблизительное значение эластичности, и погрешность будет тем больше, чем более выпуклой будет дуга АВ.

Эластичность в точке (точечная эластичность) — используется в том случае, когда задана функция спроса (предложения) и исходный уровень цены и величины спроса (или предложения). Данная формула характеризует относительное изменение объема спроса (или предложения) при бесконечно малом изменении цены (или какого-либо другого параметра).

· — производная функции спроса (или предложения) по цене;

· — рыночная цена;

· — величина спроса (или предложения) при данной цене

Условие: Пусть функция спроса имеет вид .

Оценить эластичность спроса по цене, при цене .

Решение:

· Для подсчета коэффицента эластичности нам необходимо знать и .

· При цене .

· Первая производная функции спроса .

· Подставим полученные значения в формулу точечной эластичности и получим

Ответ: Экономический смысл полученного значения заключается в том, что изменение цены на 1% относительно первоначальной цены P = 10 приведет к изменению величины спроса в противоположном направлении на 1%. Спрос характеризуется единичной эластичностью

Условие: Пусть дано уравнение спроса: P = 940 — 48*Q+Q 2

Оценить эластичность спроса по цене при объеме продаж Q = 10.

Решение:

· При Q = 10, P=940 — 48*(10)+10 2 = 560

· Теперь найдем значение dQ/dP. Однако поскольку уравнение составлено скорее для количества, чем для цены, нам следует найти значение dP/dQ:

· Математически доказано: dQ/dP = 1 / (dP / dQ)

· И это дает нам: dQ/dP = 1 / (-48 +2*Q).

· При Q = 10 получаем: dQ/dP = -1/28.

· Сделав подстановку в формулу эластичности в точке, получаем: E = (dQ/dP)*(P/Q) = (-1/28)*(560/10) = -2

Ответ: Экономический смысл полученного коэффицента заключается в том, что изменение рыночной цены на 1% относительно текущей цены P = 560, изменит величину спроса в обратном направлении на 2%. Спрос в данной точке эластичен.

Свойства эластичности

Из определения эластичности и приведенных выше формул можнор вывести основные свойства эластичности:

1. Эластичность — это безмерная величина, значение которой не зависит от того, в каких единицах мы измеряем объем, цены или какие-либо другие параметры.

2. Эластичность взаимно обратных функций — взаимно обратные величины:

· E_d — эластичность спроса по цене;

· E_p — эластичность цены по спросу;

3. В зависимости от знака при коэффициенте эластичности между рассматриваемыми факторами может иметь место:

· Прямая зависимость, когда рост одного из них вызывает увеличение другого и наоборот, например эластичность спроса на товары по потребительскому доходу E >0;

· Обратная зависимость, когда рост одного из факторов предполагает убывание другого, например эластичность спроса по ценам E 1, или эластичный спрос (предложение), когда параметр растет более высокими темпами, чем изменяется другой фактор.

· E = 1, или единичная эластичность, когда рассматриваемый параметр растет теми же темпами, что и воздействующий на него фактор;

Источник

Эластичность: понятие, виды, способы измерения. Значение расчета коэффициентов эластичности в практике менеджмента

Эластичность– мерареакции одной переменной спроса или предложения на изменение другой цены или дохода.

Эластичность изменяется в процентах.

Единичная эластичность означает что 1 процент изменения цены или дохода вызывает однопроцентной изменение спроса или предложения.

Е=1 единичная эл. 45 градусов на графике

Е>1 эластич углы острые

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у.

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у, если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

– первая производная результативной переменной у по факторной переменной x.

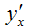
Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня

если факторная переменная х изменится на 1 % относительного своего среднего уровня

Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х:

– значение функции упри среднем значении факторной переменной х.

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии β1.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1.

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1, если факторная переменная изменится на 1 % относительно заданного уровня х1.

Общая формула для расчёта коэффициента эластичности для заданного значения х1факторной переменной х:

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х1.

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х1.

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x1:

Следовательно, Э(x1) = β1, что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.

Источник