Коэффициент бергера способ распределение мест соревнованиях среди нескольких участников

Коэффициент бергера способ распределение мест соревнованиях среди нескольких участников

Коэффициент Бергера используется для распределения мест в шахматных турнирах среди участников, набравших равное количество очков. Коэффициент Бергера участника равен сумме всех очков противников, у которых он выиграл, плюс половина суммы очков противников, с которыми он сыграл вничью.

Константин Яковлев — один из участников шахматного турнира, состоящего из 8 туров. В таблице показано количество очков, набранных в турнире соперника Константина, и результат игры с Константином.

1 — выиграл Константин,

0 — проиграл Константин.

Тур	Соперник	Очки	Результат
1	Васильев Тимур	5,0	0
2	Новикова Евгения	4,0	1
3	Тарасов Валентин	6,0	0,5
4	Павлова Анастасия	3,0	1
5	Борисов Степан	5,5	0
6	Веселов Дмитрий	5,0	0,5
7	Афанасьев Тимур	8,0	0
8	Григорьев Павел	6,0	1

Вычислите коэффициент Бергера шахматиста Константина Яковлева.

Рассчитаем коэффициент Бергера Константина Яковлева:

Источник

Коэффициенты Бухгольца и Бергера

Коэффициент Бергера

Коэффициент Бергера – способ определения мест (дополнительный коэффициент) в соревнованиях среди участников, набравших равное количество очков в основном турнирном зачете. Применяется в играх, где за победу, ничью и поражение присуждается определенное постоянное число очков (например, 1, 0.5 и 0 – в шахматах, шашках, Го, рэндзю и т.д.).

Первым такую систему подсчета очков при распределении мест предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) в августе 1873 года.

Коэффициент Бергера был первоначально разработан для круговых шахматных турниров, где каждый участник играет с каждым. Позже этот метод стали применять и для соревнований по другим играм, например, Го.

На практике коэффициент Бергера впервые применили Уильям Зонненборн (William Sonneborn) и Иоганн Бергер (Johann Berger) на турнире в Ливерпуле в 1882 году. В 1886 году распределение мест по коэффициенту Бергера было введено в регулярную практику.

Коэффициент Бергера определенного участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.

Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша с равным числом партий, например, в турнирах по швейцарской системе (хотя традиционно там применяется коэффициент Бухгольца).

Коэффициент Бухгольца

Коэффициент Бухгольца – способ определения мест (дополнительный коэффициент) в турнирах среди участников, набравших равное количество очков. Так же, как и коэффициент Бергера, применяется в играх, где за победу, ничью и поражение присуждается постоянное число очков. Однако, в отличие от коэффициента Бергера, который чаще всего применяется в круговых турнирах, коэффициент Бухгольца используется в турнирах, проводимых по швейцарской системе. В круговых турнирах система Бухгольца не применяется, т.к. в случае равенства очков в основном зачете, соперники будут иметь и равные коэффициенты.

Способ определения мест в соревнованиях среди участников, набравших равное количество очков, по коэффициенту Бухгольца был предложен в 1932 году и был назван по имени его изобретателя – шахматиста Бруно Бухгольца (Bruno Buchholz).

Коэффициент Бухгольца определенного участника складывается из суммы всех очков соперников, с которыми данный участник играл, независимо от результата встреч между ними. Идея заключается в том, что Участнику, игравшему с более сильными соперниками (соперниками, набравшими в сумме больше очков), присуждается более высокое итоговое место.

Усеченный коэффициент Бухгольца

Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется, то есть вычитают результат следующего слабейшего соперника и т.д.

Коэффициенты Бухгольца и Бергера изначально применялись только в турнирах по шахматам, однако, затем широко распространились и на другие игры, в которых результат строго фиксирован по набранным очкам (победа, поражение или ничья).

Примечание. К вопросу о расчете коэффициентов при пропуске тура и неявке соперника.

Как правило, используется следующий подход.

Все несыгранные партии (пропуск тура, неявка или нехватка соперника, «плюс») в целях подсчета коэффициентов условно считаются ничейными:

• при неявке соперника партия условно счичается ничейной
• при отсуствии соперника (при нечетном числе участников в швейцарской системе) партия считается сыгранной вничью с самим собой
• при пропуске тура в начале турнира (при опоздании) или в конце турнира (при снятии) считается, что партии сыграны вничью с самим собой

Данные меры часто необходимы, чтобы сравнивать коэффициенты участников, сыгравших разное количество партий. В противном случае, возможен вариант, например, когда один из участников набирает 7 из 10 и занимает 1 место, а второй — 7 из 7, обыграв лидера, остается только на 2 месте. начав с 4 тура, он будет иметь заведомо более низкий коэффициент. При начислении бухгольца за пропущенные туры, игрок со 100% результатом, вероятно, выйдет на 1 место, что является более справедливым.

Источник

Коэффициенты Бухгольца и Бергера

Коэффициенты Бухгольца и Бергера

Коэффициент Бергера – способ определения мест (дополнительный коэффициент) в соревнованиях среди участников, набравших равное количество очков в основном турнирном зачете. Применяется в играх, где за победу, ничью и поражение присуждается определенное постоянное число очков (например, 1, 0.5 и 0 – в шахматах, шашках, Го, рэндзю и т.д.).

Первым такую систему подсчета очков при распределении мест предложил чехословацкий шахматный мастер Оскар Гелбфус (Oskar Gelbfuhs) в августе 1873 года.
Коэффициент Бергера был первоначально разработан для круговыхшахматных турниров, где каждый участник играет с каждым. Позже этот метод стали применять и для соревнований по другим играм, например, Го.

На практике коэффициент Бергера впервые применили Уильям Зонненборн (William Sonneborn) и Иоганн Бергер (Johann Berger) на турнире в Ливерпуле в 1882 году. В 1886 году распределение мест по коэффициенту Бергера было введено в регулярную практику.
Коэффициент Бергера определенного участника складывается из суммы всех очков противников, у которых данный участник выиграл, плюс половина суммы очков противников, с которыми данный участник сыграл вничью. Идея, на которой базируется коэффициент: из двух участников, равных по числу очков, сильнее тот, кто выиграл у более сильных противников, то есть у тех, кто набрал больше очков. Поэтому участнику, имеющему больший коэффициент Бергера, присуждается более высокое итоговое место в турнире.

Коэффициент Бергера придуман для круговых турниров, но может, при необходимости, применяться и в других схемах розыгрыша с равным числом партий, например, в турнирах по швейцарской системе (хотя традиционно там применяется коэффициент Бухгольца).

Коэффициент Бухгольца – способ определения мест (дополнительный коэффициент) в турнирах среди участников, набравших равное количество очков. Так же, как и коэффициент Бергера, применяется в играх, где за победу, ничью и поражение присуждается постоянное число очков. Однако, в отличие от коэффициента Бергера, который чаще всего применяется в круговых турнирах, коэффициент Бухгольца используется в турнирах, проводимых по швейцарской системе. В круговых турнирах система Бухгольца не применяется, т.к. в случае равенства очков в основном зачете, соперники будут иметь и равные коэффициенты.

Способ определения мест в соревнованиях среди участников, набравших равное количество очков, по коэффициенту Бухгольца был предложен в 1932 году и был назван по имени его изобретателя – шахматиста Бруно Бухгольца (Bruno Buchholz).

Коэффициент Бухгольца определенного участника складывается из суммы всех очков соперников, с которыми данный участник играл, независимо от результата встреч между ними. Идея заключается в том, что Участнику, игравшему с более сильными соперниками (соперниками, набравшими в сумме больше очков), присуждается более высокое итоговое место.

Усеченный коэффициент Бухгольца

Если у двух или более участников оказываются равными и количество набранных очков, и коэффициенты Бухгольца, то из коэффициента Бухгольца каждого участника вычитают результат соперника с меньшим количеством очков. Если после такого вычитания коэффициенты Бухгольца (без результата соперника с меньшим количеством очков) остаются равными, то процедура повторяется, то есть вычитают результат следующего слабейшего соперника и т.д.

Коэффициенты Бухгольца и Бергера изначально применялись только в турнирах по шахматам, однако, затем широко распространились и на другие игры, в которых результат строго фиксирован по набранным очкам (победа, поражение или ничья).

Примечание. К вопросу о расчете коэффициентов при пропуске тура и неявке соперника.

Как правило, используется следующий подход.

Все несыгранные партии (пропуск тура, неявка или нехватка соперника, «плюс») в целях подсчета коэффициентов условно считаются ничейными:

• при неявке соперника партия условно счичается ничейной
• при отсуствии соперника (при нечетном числе участников в швейцарской системе) партия считается сыгранной вничью с самим собой
• при пропуске тура в начале турнира (при опоздании) или в конце турнира (при снятии) считается, что партии сыграны вничью с самим собой

Данные меры часто необходимы, чтобы сравнивать коэффициенты участников, сыгравших разное количество партий. В противном случае, возможен вариант, например, когда один из участников набирает 7 из 10 и занимает 1 место, а второй — 7 из 7, обыграв лидера, остается только на 2 месте. начав с 4 тура, он будет иметь заведомо более низкий коэффициент. При начислении бухгольца за пропущенные туры, игрок со 100% результатом, вероятно, выйдет на 1 место, что является более справедливым.

Источник

Коэффициент Бергера в шахматах

Раньше мы разбирались, что собой представляет коэффициент Бухгольца, где и в каких случаях он используется. Сейчас рассмотрим коэффициент Бергера, который можно считать «сводным братом» Бухгольца.

Что такое коэффициент Бергера

Коэффициент Бергера – это дополнительный числовой показатель, который необходим для ранжирования участников в турнирной таблице. Используется только в том случае, когда наблюдается равенство очков. Реализовал данную идею чех Оскар Гельбфус в далеком 1873 году. Ввели коэффициент в турнирную практику Уильям Зоннеборн и Иоганн Бергер в 1882 году на одном из турниров в Ливерпуле.

Как считать коэффициент Бергера

Для выполнения подсчетов не нужно знаний высшей математики – все можно выполнить в уме. Формула коэффициента Бергера следующая:

КБ = СуммаВ + ½ суммыН

• СуммаВ – суммарные очки соперников, с которыми зафиксирован выигрыш.
• СуммаН – суммарное количество очков противников, с которыми была сделана ничья.

Набранные очки тех противников, с которыми зафиксирован проигрыш, в счет не берутся – их сумма равняется нулю.

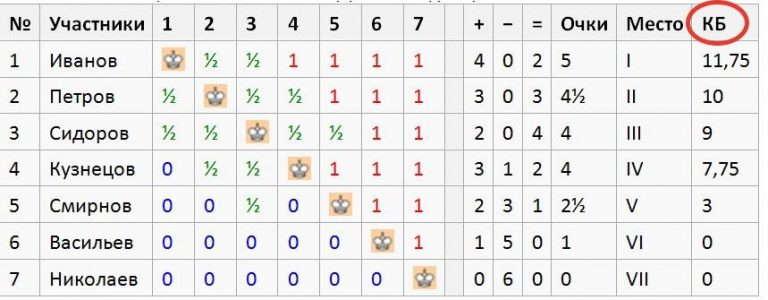
Приведем простой пример на основании вышеприведенной таблицы. Игроки Сидоров и Кузнецов имеют в своем зачете по 4 очка. Чтобы выяснить, кто из них ранжируется выше в итоговой таблице, произведем подсчет коэффициента Бергера:

Сидоров: 1 + ½*(5 +4.5 +4 +2.5) = 9

Кузнецов: (2.5 +1) + ½*(4.5 +4) = 7.75

Как можно наблюдать, Сидоров занимает более высокую позицию в финальном зачете при одинаковом количестве очков именно по Бергеру.

Когда применяется Бергер

Каждый показатель дополнительного плана, который влияет на итоговое распределение мест в турнирной таблице, должен иметь под собой логическое обоснование. «Справедливость» коэффициента Бергера заложена в формуле расчета рейтинга – преимуществом обладает тот игрок, который набрал больше очков в играх с более сильными соперниками.

Нужно отметить, что данная логика иногда вызывает ряд вопросов среди игроков. Именно из-за этого при распределении призовых позиций вошли в практику дополнительные партии, имеющие укороченный контроль. Результат за игровой доской всегда будет приоритетным. Но и без дополнительных показателей обойтись не получится (особенно во время распределения не призовых мест). За полторы сотни лет шахматисты ничего лучше коэффициента Бергера еще не придумали.

В 80-х годах стал популярным упрощенный подсчет, который заключается в том, что очки поверженных игроков идут со знаком плюс, а очки тех, кому игрок проиграл, идут со знаком минус. Конечный показатель вычисляется путем арифметического сложения.

Ошибки при подсчете

При турнирной борьбе часто возникает ситуация, когда перед заключительным туром игроки занимаются анализом коэффициентов, после чего выстраивают тактику на завершающую партию. К примеру, шахматист Иванов думает, что ему можно в последней партии сыграть вничью: «Если Петров обыграет Сидорова (с большой вероятностью) и наберет одинаковое со мной количество очков, по Бергеру я займу более высокую позицию». Иванов делает ничью в партии с прекрасными шансами и с радостью ждет награждение участников. Но при конечном просчете коэффициентов Бергера выясняется, что Петров по данному показателю его опередил.

Почему так происходит? Все элементарно. Иванов при подсчете ориентировался на коэффициенты перед последним туром, в котором проводилось множество поединков. «Очковая» масса изменилась, что и повлекло за собой проигрыш Иванова. Хорошо, когда в команде есть помощник, который ведет подсчет коэффициентов Бергера во время последнего тура в режиме онлайн и передает результаты игроку. Но отвлекаться на данные вещи во время партии не стоит, ведь гораздо надежнее все решать за шахматной доской.

Источник