- Равномерные и неравномерные коды.
- Кодирование информации
- Содержание
- Код [ править ]
- Виды кодов [ править ]
- Примеры кодов [ править ]
- Однозначно декодируемый код [ править ]
- Префиксный код [ править ]
- Пример кодирования [ править ]
- Преимущества префиксных кодов [ править ]
- Недостатки префиксных кодов [ править ]
- Пример неудачного декодирования [ править ]
- Не префиксный однозначно декодируемый код [ править ]
- Практическая работа № 13 построение кода постоянной длины построение кода переменной длины
Равномерные и неравномерные коды.
Дата добавления: 2015-08-14 ; просмотров: 33968 ; Нарушение авторских прав
Код называется равномерным (или кодом постоянной длины), если все его кодовые слова содержат одинаковое число букв (одинаковую длину слов). Соответственно, кодирование называется равномерным, если соответствующий ему код имеет постоянную длину. В настоящее время в информатике более употребительно равномерное кодирование, оно проще и более удобно. В компьютерах при кодировании информации в основном используются равномерные коды, соответствующие размерам компьютерных ячеек.
К равномерным кодам относится телеграфный код Бодо (Baudot code). Его можно считать двоичным равномерным алфавитным кодом. Первоначальный вариант этого кода разработал Эмиль Бодо в 1870 году для своего телеграфа. Код вводился прямо клавиатурой, состоящей из пяти клавиш, нажатие или ненажатие клавиши соответствовало передаче или непередаче одного бита в пятибитном коде. Например, буква А передавалась как — — + — — , что соответствовало нажатию средней клавиши. В двоичном коде это можно записать как 00100. Таким образом, каждая буква записывалась пятью битами. Следовательно, кодом Бодо можно было передать 2 5 =32 различных символа.
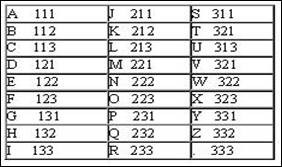
Другим интересным примером равномерного кода является код Трисиме, в котором знакам латинского алфавита ставятся в соответствие кодовые слова длины 3 над алфавитом из 3-х символов: <1, 2, 3>. Этот код представлен в следующей таблице :
Понятно, что код Трисиме не может кодировать более чем 3 3 =27 символов.
Число букв в алфавите кода называется основанием кода, а длина кодовых слов равномерного кода называется порядком кода. Коды с основанием 2, как уже говорилось, называются двоичными, а с основанием 3 – троичными, и так далее. Так код Бодо имеет основание 2, а порядок 5, а у кода Трисиме и основание, и порядок равны 3.
Код называется неравномерным (или кодом переменной длины), если его кодовые слова имеют разное число букв (неодинаковую длину слов). Соответственно, кодирование называется неравномерным, если соответствующий ему код неравномерный.
Типичным примером неравномерного кода является телеграфный код, который принято называть азбукой Морзе. На следующей таблице представлен код азбуки Морзе для русского алфавита:
| A | • − | И | • • | P | • − • | Ш | − − − − | • − − − − | − − − − • | |
| Б | − • • • | Й | • − − − | С | • • • | Щ | − − • − | • • − − − | − − − − − | |
| В | • − − | К | − • − | Т | − | Ъ | • − − • − • | • • • − − | Точка | • • • • • • |
| Г | − − • | Л | • − • • | У | • • − | Ь | − • • − | • • • • − | Запятая | • − • − • − |
| Д | − • • | М | − − | Ф | • • − • | Ы | − • − − | • • • • • | / | − • • − • |
| Е | • | H | − • | Х | • • • • | Э | • • − • • | − • • • • | ? | • • − − • • |
| Ж | • • • − | О | − − − | Ц | − • − • | Ю | • • − − | − − • • • | ! | − − • • − − |
| З | − − • • | П | • − − • | Ч | − − − • | Я | • − • − | − − − • • | @ | • − − • − • |
Как видим, азбука Морзе состоит из слов над алфавитом из двух символов: точка и тире. Но, строго говоря, этот код не является двоичным, так как он при кодировании слов предполагает еще один символ для разделения букв в слове (символ «пауза»). Без этого символа не было бы однозначности при декодировании текстов. Например, код из четырех тире можно было бы декодировать по-разному: или как код одной буквы Ш, или как код сочетаний из двух букв — ММ, ОТ или ТО. Разделяющий символ позволяет однозначно декодировать любую кодовую последовательность, полученную кодированием сообщений при помощи азбуки Морзе, но тогда код азбуки Морзе следует считать троичным, так как его алфавит содержит три символа.
Американский изобретатель телеграфа Сэмюель Морзе разработал этот код в 1838 году для передачи телеграфных сообщений в виде последовательности электрических сигналов, передаваемых от одного телеграфного аппарата по проводам к другому телеграфному аппарату. Этот код был придуман Морзе задолго до научных исследований
 |
| СэмюэлМорзе (1791-1872) |
относительной частоты появления различных букв в текстах, но, тем не менее, Морзе при составлении кода использовал принцип частоты букв. Буквам, используемым чаще, им присвоены короткие кодовые комбинации, редко используемым буквам – длинные. Морзе оценил относительную частоту букв английского языка подсчетом литер в ячейках типографской наборной машины. Наиболее часто используемой букве «Е» (в английском языке) он присвоил наиболее короткий код «точка». Следующей по количеству литер букве он присвоил код несколько большей длительности и так далее.
При составлении азбуки Морзе для букв русского алфавита учет относительной частоты букв не производился, и это повысило его избыточность. Расчеты избыточности кода Морзе на основании проведенных исследований частоты появления букв показали, что для букв английского алфавита она составляет 19%, для букв русского алфавита 22%.
Самым знаменитым телеграфным сообщением является сигнал бедствия «SOS» (Save Our Souls — спасите наши души). Вот как он выглядит: «• • • – – – • • •»
Преимущество у неравномерных кодов перед равномерными как раз и состоит в том, что сообщения можно передавать более экономным способом, так как часто передаваемые кодовые слова более короткие, а значит, кодовая последовательность может иметь меньшую длину, чем для равномерных кодов. Ниже это будет показано.
Но у неравномерных кодов есть серьезный недостаток по сравнению с равномерными кодами. У равномерных кодов кодовая последовательность всегда декодируется однозначно за счет того, что кодовые слова имеют одинаковую длину (кодовая последовательность легко делится на кодовые слова). Но не для всех неравномерных кодов достигается однозначность декодирования кодовых последовательностей. Мы уже видели это, пытаясь рассматривать азбуку Морзе как двоичный код.
Приведем более простой пример. Пусть S =
Этот код неравномерный (кодовые слова разной длины).
Закодируем последовательность сообщений: s7s7. Имеем F(s7s7)=B=111111. Но эта последовательность может быть декодирована и по-другому, так как: B=F(s3s3s3)= F(s1s3s7)=F(s3s7s1)=F(s1s1s1s1s1s1s1s). Как видим, способов декодирования много (подсчитайте: сколько их?). Неоднозначно декодируется и следующая последовательность:
11011011 (а сколько здесь способов декодирования?). Очевидно, что такой код практически использовать нельзя. А если мы изменим код так, чтобы он стал равномерным, например, доопределим функцию F так:
то теперь никаких проблем с декодированием не будет.
Источник
Кодирование информации
| Определение: |
| Кодирование информации (англ. information coding) — отображение данных на кодовые слова. |
Обычно в процессе кодирования информация преобразуется из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения или автоматической обработки. В более узком смысле кодированием информации называют представление информации в виде кода. Средством кодирования служит таблица соответствия знаковых систем, которая устанавливает взаимно однозначное соответствие между знаками или группами знаков двух различных знаковых систем.
Содержание
Код [ править ]
| Определение: |
| Пусть [math]U[/math] — множество исходных символов, [math]Z[/math] — кодовый алфавит, [math]Z^*[/math] — множество всех строк конечной длины из [math]Z[/math] . Код (англ. code) — отображение [math]c : U \rightarrow Z^*[/math] и [math]c^* : U^* \rightarrow Z^*[/math] так, что [math]c^*(x_1 x_2 . x_n) = c(x_1)c(x_2)..c(x_n)[/math] |
Виды кодов [ править ]
- Код фиксированной длины (англ. fixed-length code) — кодирование каждого символа производится с помощью строк одинаковой длины. Также он называется равномерным или блоковым кодом.
- Код переменной длины (англ. variable-length code) — кодирование производится с помощью строк переменной длины. Также называется неравномерным кодом.
- Префиксный код — код, в котором, никакое кодовое слово не является началом другого. Аналогично, можно определить постфиксный код — это код, в котором никакое кодовое слово не является концом другого.
Все вышеперечисленные коды являются однозначно декодируемыми — для такого кода любое слово, составленное из кодовых слов, можно декодировать только единственным способом.
Примеры кодов [ править ]
- ASCII — блочный.
- Код Хаффмана (англ. Huffman code) — префиксный.
- Азбука Морзе — не является ни блочным, ни префиксным, тем не менее, однозначно декодируемый засчет использования пауз.
Однозначно декодируемый код [ править ]
| Определение: |
| Однозначно декодируемый код (англ. uniquely decodable code) — код, в котором любое слово составленное из кодовых слов можно декодировать только единственным способом. |
Пусть есть код заданный следующей кодовой таблицей:
[math]a_1 \rightarrow b_1[/math]
[math]a_2 \rightarrow b_2[/math]
[math]a_k \rightarrow b_k[/math]
Код является однозначно декодируемым, только тогда, когда для любых строк, составленных из кодовых слов, вида:
Всегда выполняются равенства:
Заметим, что если среди кодовых слов будут одинаковые, то однозначно декодировать этот код мы уже не сможем.
Префиксный код [ править ]
| Определение: |
| Префиксный код (англ. prefix code) — код, в котором никакое кодовое слово не является префиксом какого-то другого кодового слова. |
Предпочтение префиксным кодам отдается из-за того, что они упрощают декодирование. Поскольку никакое кодовое слово не выступает в роли префикса другого, кодовое слово, с которого начинается файл, определяется однозначно, как и все последующие кодовые слова.
Пример кодирования [ править ]
[math] c(a) = 00 [/math]
[math] c(b) = 01 [/math]
[math] c(c) = 1 [/math]
Закодируем строку [math]abacaba[/math] :
Такой код можно однозначно разбить на слова:
[math]00\ 01\ 00\ 1\ 00\ 01\ 00[/math]
Преимущества префиксных кодов [ править ]
- Однозначно декодируемый и разделимый
- Удается получить более короткие коды, чем с помощью кода фиксированной длины.
- Возможности декодировки сообщения, не получая его целиком, а по мере его поступления.
Недостатки префиксных кодов [ править ]
- При появлении ошибок в кодовой комбинации, при определенных обстоятельствах, может привести к неправильному декодированию не только данной, но и последующей кодовой комбинации, в отличии от равномерных кодов, где ошибка в кодовой комбинации приводит к неправильному декодированию только ее.
Пример неудачного декодирования [ править ]
Предположим, что последовательность [math]abacaba[/math] из примера передалась неверно и стала:
[math]c^<**>(abacaba) = 0001001\ 1\ 00100[/math]
Разобьем ее согласно словарю:
[math] 00\ 01\ 00\ 1\ 1\ 00\ 1\ 00[/math]
[math]a\quad b\quad a\ c\ c\quad a\ c\ a[/math]
Полученная строка совпадает только в битах, которые находились до ошибочного, поэтому декодирование неравномерного кода, содержащего ошибки, может дать абсолютно неверные результаты.
Не префиксный однозначно декодируемый код [ править ]
Как уже было сказано, префиксный код всегда однозначно декодируем. Обратное в общем случае неверно:
[math] c(a) = 1 [/math]
[math] c(b) = 12 [/math]
[math] c(c) = 31 [/math]
Закодируем [math]abbca[/math] , получим кодовую строку: [math]11212311[/math]
Мы можем ее однозначно декодировать, так как знаем, что слева от двойки и справа от тройки всегда стоит единица.
После декодирования получаем: [math]abbca[/math]
Источник
Практическая работа № 13 построение кода постоянной длины построение кода переменной длины
Практическая работа № 13
Построение кода постоянной длины. Построение кода переменной длины.
Цель работы: Изучить методы построения кода постоянной длины и переменной длины. Оценить эффективность полученного кода.
1. Для изображения информации часто используются тексты на том или ином языке. Множество букв алфавита языка конечно и может быть записано в виде двоичных кодов. Существует стандартная кодировка букв английского алфавита ASCII (American Standard Code for Information Interchange — Американский стандартный код для обмена информацией). Это семибитный код, в котором кроме букв английского алфавита (строчных и прописных) представлены также цифры, знаки препинания, некоторые дополнительные знаки и управляющие коды (например, перевод строки).
Для представления букв других алфавитов (кроме английского) используется расширение кода ASCII до 8-битового (extended ASCII); при этом литеры дополнительного алфавита кодируются двоичными числами, старший бит которых равен 1, тогда как для исходных кодов ASCII он равен 0.
Код постоянной длины – двоичное кодирование, отображающее каждый кодируемый знак на двоичное слово одинаковой длины. Пусть объектом кодирования являются тексты, записанные на некотором (естественном или искусственном) языке, причем число букв в алфавите этого языка, включая (если есть такая необходимость) некоторые знаки препинания, знак пробела и т. п., равно n. Далее, пусть L – наименьшее натуральное число, удовлетворяющее условию:
Тогда можно пользоваться простейшим методом побуквенного кодирования с помощью кода постоянной длины L. Наиболее компактное кодирование достигается в том случае, когда число букв в алфавите равняется целой степени двойки. Нарушение этого условия непременно приводит к некоторой избыточности.
Стохастический источник сообщений генерирует тексты в виде последовательности символов с заданным алфавитом и стационарными (не зависящими от времени) статистическими характеристиками появления элементов алфавита в последовательности. В простейшем случае каждый символ aiОA появляется независимо от других с вероятностью p(i).
Количество информации, приносимое в среднем одним элементом сообщения (текста), по определению равно энтропии источника:
Энтропия источника H является непрерывной функцией от p(i). При фиксированном n энтропия максимальна и равна log2 n в случае, если все p(i) равны между собой. Обозначим длину i-го кодового слова как |cod(ai)|.
Средняя длина кодовых слов может быть определена следующим образом:
Эффективность кода: отношение H/L
Избыточность кода: отношение (L–H)/L
Пример расчета эффективности кода постоянной длины
Источник