Главная » Разное

Кодирование по способу хаффмана

Содержание
  1. Алгоритм Хаффмана
  2. Содержание
  3. Определение [ править ]
  4. Алгоритм построения бинарного кода Хаффмана [ править ]
  5. Время работы [ править ]
  6. Пример [ править ]
  7. Корректность алгоритма Хаффмана [ править ]
  8. Код Хаффмана
  9. Код Хаффмана
  10. Таблица вероятности символов
  11. Таблица вероятности символов
  12. Импортировать данные Ошибка импорта
  13. Кодирование Хаффмана
  14. Содержание
  15. Алгоритм
  16. Построение дерева Хаффмана
  17. Пример реализации
  18. Ссылки
  19. Литература
  20. Полезное
  21. Смотреть что такое «Кодирование Хаффмана» в других словарях:

Алгоритм Хаффмана

Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.

Содержание

Определение [ править ]

Определение:
Пусть [math]A=\,a_<2>, \ldots ,a_\>[/math] — алфавит из [math]n[/math] различных символов, [math]W=\,w_<2>, \ldots ,w_\>[/math] — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов [math]C=\,c_<2>, \ldots ,c_\>[/math] , где [math]c_[/math] является кодом для символа [math]a_[/math] , такой, что:
  • [math]c_[/math] не является префиксом для [math]c_[/math] , при [math]i \ne j[/math] ,
  • cумма [math]\sum\limits_ w_\cdot |c_|[/math] минимальна ( [math]|c_|[/math] — длина кода [math]c_[/math] ),

называется кодом Хаффмана.

Алгоритм построения бинарного кода Хаффмана [ править ]

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

  1. Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
  2. Из списка выберем два узла с наименьшим весом.
  3. Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
  4. Добавим к списку только что сформированный узел вместо двух объединенных узлов.
  5. Если в списке больше одного узла, то повторим пункты со второго по пятый.

Время работы [ править ]

Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время [math]O(N \log N)[/math] .Такую асимптотику можно улучшить до [math]O(N)[/math] , используя обычные массивы.

Пример [ править ]

Закодируем слово [math]abracadabra[/math] . Тогда алфавит будет [math]A= \ [/math] , а набор весов (частота появления символов алфавита в кодируемом слове) [math]W=\<5, 2, 2, 1, 1\>[/math] :

В дереве Хаффмана будет [math]5[/math] узлов:

Узел a b r с d
Вес 5 2 2 1 1

По алгоритму возьмем два символа с наименьшей частотой — это [math]c[/math] и [math]d[/math] . Сформируем из них новый узел [math]cd[/math] весом [math]2[/math] и добавим его к списку узлов:

Узел a b r cd
Вес 5 2 2 2

Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :

Узел a rcd b
Вес 5 4 2

Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :

Узел brcd a
Вес 6 5

На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :

Узел abrcd
Вес 11

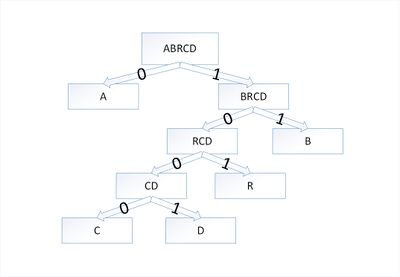
Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):

Символ a b r с d
Код 0 11 101 1000 1001

Таким образом, закодированное слово [math]abracadabra[/math] будет выглядеть как [math]01110101000010010111010[/math] . Длина закодированного слова — [math]23[/math] бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы [math]33[/math] бита, что существенно больше.

Корректность алгоритма Хаффмана [ править ]

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Доказательство: [math]\triangleright[/math]

Возьмем дерево [math]T[/math] , представляющее произвольный оптимальный префиксный код для алфавита [math]C[/math] . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] — листья с общим родительским узлом, находящиеся на максимальной глубине.

Пусть символы [math]a[/math] и [math]b[/math] имеют общий родительский узел и находятся на максимальной глубине дерева [math]T[/math] . Предположим, что [math]f[a] \leqslant f[b][/math] и [math]f[x] \leqslant f[y][/math] . Так как [math]f[x][/math] и [math]f[y][/math] — две наименьшие частоты, а [math]f[a][/math] и [math]f[b][/math] — две произвольные частоты, то выполняются отношения [math]f[x] \leqslant f[a][/math] и [math]f[y] \leqslant f[b][/math] . Пусть дерево [math]T'[/math] — дерево, полученное из [math]T[/math] путем перестановки листьев [math]a[/math] и [math]x[/math] , а дерево [math]T»[/math] — дерево полученное из [math]T'[/math] перестановкой листьев [math]b[/math] и [math]y[/math] . Разность стоимостей деревьев [math]T[/math] и [math]T'[/math] равна:

[math]B(T) — B(T’) = \sum\limits_ f(c)d_T(c) — \sum\limits_ f(c)d_(c) = (f[a] — f[x])(d_T(a) — d_T(x)),[/math]

что больше либо равно [math]0[/math] , так как величины [math]f[a] — f[x][/math] и [math]d_T(a) — d_T(x)[/math] неотрицательны. Величина [math]f[a] — f[x][/math] неотрицательна, потому что [math]x[/math] — лист с минимальной частотой, а величина [math]d_T(a) — d_T(x)[/math] является неотрицательной, так как лист [math]a[/math] находится на максимальной глубине в дереве [math]T[/math] . Точно так же перестановка листьев [math]y[/math] и [math]b[/math] не будет приводить к увеличению стоимости. Таким образом, разность [math]B(T’) — B(T»)[/math] тоже будет неотрицательной.

Таким образом, выполняется неравенство [math]B(T») \leqslant B(T)[/math] . С другой стороны, [math]T[/math] — оптимальное дерево, поэтому должно выполняться неравенство [math]B(T) \leqslant B(T»)[/math] . Отсюда следует, что [math]B(T) = B(T»)[/math] . Значит, [math]T»[/math] — дерево, представляющее оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] имеют одинаковую максимальную длину, что и доказывает лемму. [math]\triangleleft[/math]

Лемма (2):
Доказательство:
[math]\triangleright[/math]

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] может быть выражена через стоимость [math]B(T’)[/math] дерева [math]T'[/math] . Для каждого символа [math]c \in C \backslash \[/math] верно [math]d_T(C) = d_[/math] , значит, [math]f[c]d_T(c) = f[c]d_(c)[/math] . Так как [math]d_T(x) = d_T(y) = d_ (z) + 1[/math] , то

[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_(z) + 1) = f[z]d_(z) + (f[x] + f[y])[/math]

из чего следует, что

[math] B(T) = B(T’) + f[x] + f[y] [/math]

[math] B(T’) = B(T) — f[x] — f[y] [/math]

Докажем лемму от противного. Предположим, что дерево [math]T[/math] не представляет оптимальный префиксный код для алфавита [math]C[/math] . Тогда существует дерево [math]T»[/math] такое, что [math]B(T») \lt B(T)[/math] . Согласно лемме (1), элементы [math]x[/math] и [math]y[/math] можно считать дочерними элементами одного узла. Пусть дерево [math]T»'[/math] получено из дерева [math]T»[/math] заменой элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y][/math] . Тогда

[math]B(T»’) = B(T») — f[x] — f[y] \lt B(T) — f[x] — f[y] = B(T’)[/math] ,

Источник

Код Хаффмана

Построение кода Хаффмана для таблицы вероятностей.

Вот калькулятор, который рассчитывает коды Хаффмана для заданной вероятности символов.
Немного теории под калькулятором.

Код Хаффмана

Таблица вероятности символов

Таблица вероятности символов

Импортировать данные Ошибка импорта

Небольшой отрывок из Википедии.

Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.

Этот метод кодирования состоит из двух основных этапов:
Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.

Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности (т. е. ни одно кодовое слово не является префиксом другого), что позволяет однозначно их декодировать.
Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).

  1. Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
  2. Выбираются два свободных узла дерева с наименьшими весами.
  3. Создается их родитель с весом, равным их суммарному весу.
  4. Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
  5. Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.
  6. Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.

Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n0 потомков — символы из предыдущего шага и т. д.

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от корня до листа дерева, соответствующего текущему символу, накапливая биты при перемещении по ветвям дерева (первая ветвь в пути соответствует младшему биту). Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Источник

Кодирование Хаффмана

Алгоритм Хаффмана (англ. Huffman ) — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году доктором Массачусетского технологического института Дэвидом Хаффманом. В настоящее время используется во многих программах сжатия данных.

В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m2 с более чем двумя символами.

Этот метод кодирования состоит из двух основных этапов:

  1. Построение оптимального кодового дерева.
  2. Построение отображения код-символ на основе построенного дерева.

Содержание

Алгоритм

  1. Подсчитываются вероятности появления символов первичного алфавита в исходном тексте (если они не заданы заранее)
  2. Символы первичного алфавита m1 выписывают в порядке убывания вероятностей.
  3. Последние n0 символов объединяют в новый символ, вероятность которого равна суммарной вероятности этих символов, удаляют эти символы и вставляют новый символ в список остальных на соответствующее место (по вероятности). n0 вычисляется из системы:
    ,
    где a — целое число, m1 и m2 — мощность первичного и вторичного алфавита соответственно.
  4. Последние m2 символов снова объединяют в один и вставляют его в соответствующей позиции, предварительно удалив символы, вошедшие в объединение.
  5. Предыдущий шаг повторяют до тех пор, пока сумма всех m2 символов не станет равной 1.

Этот процесс можно представить как построение дерева, корень которого — символ с вероятностью 1, получившийся при объединении символов из последнего шага, его m2 потомков — символы из предыдущего шага и т. д.

Каждые m2 элементов, стоящих на одном уровне, нумеруются от 0 до m2-1. Коды получаются из путей (от первого потомка корня и до листка). При декодировании можно использовать то же самое дерево, считывается по одной цифре и делается шаг по дереву, пока не достигается лист — тогда выводится символ, стоящий в листе и производится возврат в корень.

Построение дерева Хаффмана

Бинарное дерево, соответствующее коду Хаффмана, называют деревом Хаффмана.

Задача построения кода Хаффмана равносильна задаче построения соответствующего ему дерева.

Общая схема построения дерева Хаффмана:

  1. Составим список кодируемых символов (при этом будем рассматривать каждый символ как одноэлементное бинарное дерево, вес которого равен весу символа).
  2. Из списка выберем 2 узла с наименьшим весом (под весом можно понимать частоту использования символа — чем чаще используется, тем больше весит).
  3. Сформируем новый узел и присоединим к нему, в качестве дочерних, два узла выбранных из списка. При этом вес сформированного узла положим равным сумме весов дочерних узлов.
  4. Добавим сформированный узел к списку.
  5. Если в списке больше одного узла, то повторить 2-5.

Пример реализации

Пример реализации алгоритма Хаффмана на языке

Пример реализации алгоритма Хаффмана на языке Delphi

Результат работы для строки «to be or not to be?». Выводятся: символ, его вес и двоичный код. Далее закодированная строка и результат декодирования.

Соответствующее дерево Хаффмана.

Ссылки

Литература

  • Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: «Вильямс», 2006. — 1296 с. — ISBN 0-07-013151-1
  • Д. Сэломон. Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — 368 с. — 3000 экз. — ISBN 5-94836-027-X
  • Ананий В. Левитин. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: «Вильямс», 2006. — С. 392—398. — ISBN 0-201-74395-7
Методы сжатия
Теория
Информация Собственная · Взаимная · Энтропия · Условная энтропия · Сложность · Избыточность
Единицы измерения Бит · Нат · Ниббл · Хартли · Формула Хартли
Без потерь
Энтропийное сжатие Алгоритм Хаффмана · Адаптивный алгоритм Хаффмана · Арифметическое кодирование (Алгоритм Шеннона — Фано · Интервальное) · Коды Голомба · Дельта · Универсальный код (Элиаса · Фибоначчи)
Словарные методы RLE · · LZ ( · LZSS · LZW · LZWL · · · LZX · LZRW · LZJB · LZT)
Прочее RLE · CTW · BWT · PPM · DMC
Аудио
Теория Свёртка · PCM · Алиасинг · Дискретизация · Теорема Котельникова
Методы LPC (LAR · LSP) · WLPC · CELP · ACELP · A-закон · μ-закон · MDCT · Преобразование Фурье · Психоакустическая модель
Прочее Dynamic range compression · Сжатие речи · Полосное кодирование
Изображения
Термины Цветовое пространство · Пиксел · Chroma subsampling · Артефакты сжатия
Методы RLE · DPCM · Фрактальный · Wavelet · EZW · SPIHT · LP · ДКП · ПКЛ
Прочее Битрейт · Test images · PSNR · Квантование
Видео
Термины Характеристики видео · Кадр · Типы кадров · Качество видео
Методы Компенсация движения · ДКП · Квантование
Прочее Видеокодек · Rate distortion theory (CBR · ABR · VBR)
См. также: Программы для сжатия данных • Стандарты и форматы сжатия

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Кодирование Хаффмана» в других словарях:

Кодирование энтропии — кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных коды, длины которых… … Википедия

Кодирование с минимальной избыточностью — Кодирование энтропии кодирование словами (кодами) переменной длины, при которой длина кода символа имеет обратную зависимость от вероятности появления символа в передаваемом сообщении. Обычно энтропийные кодировщики используют для сжатия данных… … Википедия

Кодирование длин серий — (англ. Run length encoding, RLE) или Кодирование повторов простой алгоритм сжатия данных, который оперирует сериями данных, то есть последовательностями, в которых один и тот же символ встречается несколько раз подряд. При кодировании… … Википедия

кодирование по алгоритму Хаффмана — Метод сжатия данных, при котором часто встречающиеся символы кодируются более эффективно и занимают меньше места, чем данные, встречающиеся реже. Является технологией сжатия без потери данных (в отличие от JPEG компрессии, при которой происходит… … Справочник технического переводчика

кодирование по способу Хаффмана — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN variable length codingVLC … Справочник технического переводчика

Кодирование Шеннона-Фано — Алгоритм Шеннона Фано один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Данный метод сжатия имеет большое сходство с алгоритмом Хаффмана, который появился на несколько лет позже. Алгоритм… … Википедия

Кодирование Голомба — Коды Голомба это семейство энтропийных кодеров, являющихся общим случаем унарного кода. Также под кодом Голомба может подразумеваться один из представителей этого семейства. Код Голомба позволяет представить последовательность символов в виде… … Википедия

Код Хаффмана — Алгоритм Хаффмана адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им … Википедия

Арифметическое кодирование — Арифметическое кодирование один из алгоритмов энтропийного сжатия. В отличие от алгоритма Хаффмана, не имеет жесткого постоянного соответствия входных символов группам бит выходного потока. Это даёт алгоритму большую гибкость в… … Википедия

Энтропийное кодирование — Для термина «Кодирование» см. другие значения. Энтропийное кодирование кодирование последовательности значений с возможностью однозначного восстановления с целью уменьшения объёма данных (длины последовательности) с помощью усреднения… … Википедия

Источник

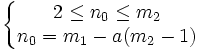Читайте также:  Демократический способ выработки управленческих решений
Оцените статью
Разные способы
© 2024 Разные способы.
Внимание! Информация, опубликованная на сайте, носит исключительно ознакомительный характер и не является рекомендацией к применению.