Кодирование и шифрование — в чём разница?
Одно делается для удобства, а другое — для защиты.
👉 Эта статья — для расширения кругозора. Если нужна практика, заходите в раздел «Это баг», там вагон практики.
«Данные закодированы» и «данные зашифрованы» — это не одно и то же. После этой статьи вы тоже сможете различать эти два подхода к данным.
Кодирование
Кодирование — это представление данных в каком-то виде, с которым удобно работать человеку или компьютеру.
Кодирование нужно для того, чтобы все, кто хочет, могли получать, передавать и работать с данными так, как им хочется. Благодаря кодированию мы можем обмениваться данными между собой — мы просто кодируем их в понятном для всех виде.
Например, древний человек видит волка, это для него данные. Ему нужно передать данные своему племени. Он произносит какой-то звук, который у других его соплеменников вызывает ассоциации с понятием «волк» или «опасность». Все мобилизуются. В нашем случае звук — это был способ кодирования.

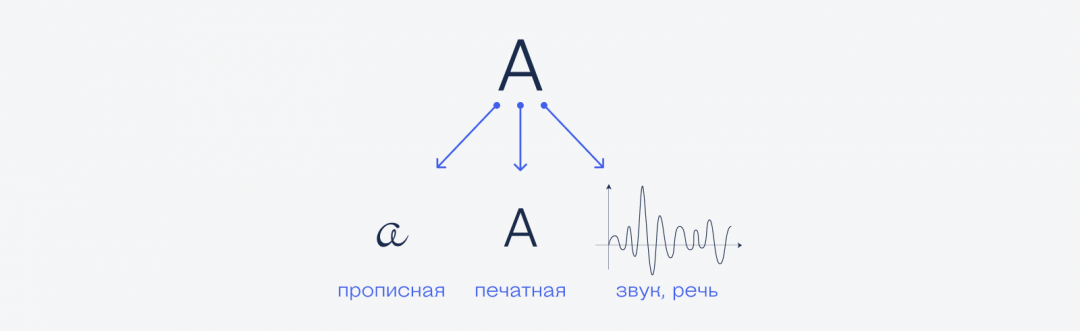
Для следующего примера возьмём букву «а». Её можно произнести как звук — это значит, что мы закодировали эту букву в виде звуковой волны. Также эту букву можно написать прописью или в печатном виде. Всё это примеры кодирования буквы «а», удобные для человека.
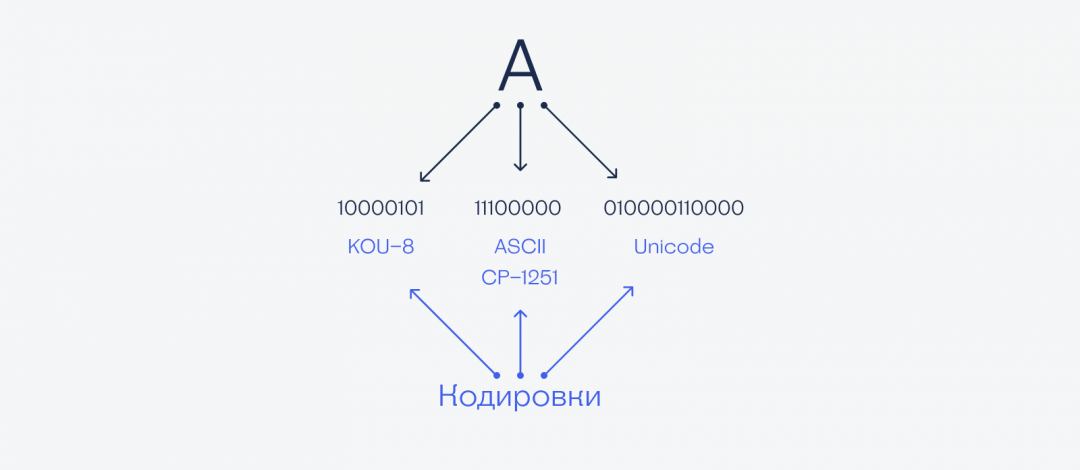
В компьютере буква «а» кодируется по-разному, в зависимости от выбранной кодировки внутри операционной системы:
Кодирование — это то, как удобнее воспринимать информацию тем, кто ей пользуется. Например, моряки кодируют букву «а» последовательностью из короткого и длинного сигнала или точкой и тире. На языке жестов, которым пользуются глухонемые, она обозначается сложенными почти в кулак пальцами.
Сломанная кодировка
Когда встречаем незнакомую кодировку, то можно подумать, что перед нами зашифрованные данные. Например, если посмотреть на двух людей, которые общаются языком жестом, можно подумать, что они зашифровали своё общение. На самом деле вы просто не были готовы воспринимать информацию в этой кодировке.
Похожая ситуация в компьютере. Допустим, вы увидели такой текст:
рТЙЧЕФ, ЬФП ЦХТОБМ лПД!
Здесь написано «Привет, это журнал Код!», только в кодировке КОИ-8, которую интерпретировали через кодировку CP-1251. Компьютер не знал, какая здесь должна быть кодировка, поэтому взял стандартную для него CP-1251, посмотрел символы по таблице и выдал то, что получилось. Если бы компьютер знал, что для этой кодировки нужна другая таблица, мы бы всё прочитали правильно с первого раза.
Ещё кодирование
Кодированием пользуется весь мир на протяжении всей своей истории:
- наскальные рисунки кодируют истории древних людей;
- египетская клинопись на табличках и берестяные грамоты — примеры алфавитного кодирования. Обычно нужны были, чтобы закодировать и зафиксировать численность голов скота и мешков зерна;
- ноты у музыкантов — кодируют музыку, а точнее, инструкцию по исполнению музыки;
- дорожные знаки и сигналы светофора кодируют правила дорожного движения;
- иконки в смартфоне — тоже пример кодирования;
- разные народы кодируют одни и те же слова по-разному, каждый на своём языке;
- значки на ярлычке одежды кодируют информацию о том, как стирать и ухаживать за вещью.
👉 Кодирование нужно для того, чтобы сделать данные максимально понятным для получателя и для всех, кто тоже использует такие же обозначения.
Шифрование
Если кодирование нужно, чтобы сделать информацию понятной для всех, то шифрование работает наоборот — прячет данные от всех, у кого нет ключа расшифровки.
Задача шифрования — превратить данные, которые могут прочитать все, в данные, которые может прочитать только тот, у кого есть специальное знание (ключ безопасности, сертификат, пароль или расшифровочная матрица). Если пароля нет, то данные внешне представляют из себя полную бессмыслицу, например:
Здесь зашифрована та же самая фраза — «Привет, это журнал Код!». Но не зная ключа для расшифровки и принципа шифрования, вы не сможете её прочитать.
Шифрование нужно, например, чтобы передать данные от одного к другому так, чтобы по пути их никто не прочитал. Шифрование используют:
- госорганы, чтобы защитить персональные данные граждан;
- банки, чтобы хранить информацию о клиентах и о переводах денег;
- мессенджеры, чтобы защитить переписку;
- сайты;
- мобильные приложения;
- и всё остальное, что связано с безопасностью или тайнами.
Шифрование бывает аналоговое и компьютерное, простое и сложное, взламываемое и нет. Обо всём этом ещё расскажем, подписывайтесь.
Источник
Кодирование информации код способы кодирования шифрование
22. КОДИРОВАНИЕ ИНФОРМАЦИИ
22.1. Общие сведения
Кодирование – представление информации в альтернативном виде. По своей сути кодовые системы (или просто коды) аналогичны шифрам однозначной замены, в которых элементам кодируемой информации соответствуют кодовые обозначения. Отличие заключается в том, что в шифрах присутствует переменная часть (ключ), которая для определенного исходного сообщения при одном и том же алгоритме шифрования может выдавать разные шифртексты. В кодовых системах переменной части нет. Поэтому одно и то же исходное сообщение при кодировании, как правило, всегда выглядит одинаково 1 . Другой отличительной особенностью кодирования является применение кодовых обозначений (замен) целиком для слов, фраз или чисел (совокупности цифр). Замена элементов кодируемой информации кодовыми обозначениями может быть выполнена на основе соответствующей таблицы (наподобие таблицы шифрозамен) либо определена посредством функции или алгоритма кодирования.
В качестве элементов кодируемой информации могут выступать:
— буквы, слова и фразы естественного языка;
— различные символы, такие как знаки препинания, арифметические и логические операции, операторы сравнения и т.д. Следует отметить, что сами знаки операций и операторы сравнения – это кодовые обозначения;
— ситуации и явления;
Кодовые обозначения могут представлять собой:
— буквы и сочетания букв естественного языка;
— световые и звуковые сигналы;
— набор и сочетание химических молекул;
Кодирование может выполняться в целях:
— удобства хранения, обработки и передачи информации (как правило, закодированная информация представляется более компактно, а также пригодна для обработки и передачи автоматическими программно-техническими средствами);
— удобства информационного обмена между субъектами;
— идентификации объектов и субъектов;
— сокрытия секретной информации;
Кодирование информации бывает одно- и многоуровневым. Примером одноуровневого кодирования служат световые сигналы, подаваемые светофором (красный – стой, желтый – приготовиться, зеленый – вперед). В качестве многоуровневого кодирования можно привести представление визуального (графического) образа в виде файла фотографии. Вначале визуальная картинка разбивается на составляющие элементарные элементы (пикселы), т.е. каждая отдельная часть визуальной картинки кодируется элементарным элементом. Каждый элемент представляется (кодируется) в виде набора элементарных цветов (RGB: англ. red – красный, green – зеленый, blue – синий) соответствующей интенсивностью, которая в свою очередь представляется в виде числового значения. Впоследствии наборы чисел, как правило, преобразуются (кодируются) с целью более компактного представления информации (например, в форматах jpeg, png и т.д.). И наконец, итоговые числа представляются (кодируются) в виде электромагнитных сигналов для передачи по каналам связи или областей на носителе информации. Следует отметить, что сами числа при программной обработке представляются в соответствии с принятой системой кодирования чисел.
Кодирование информации может быть обратимым и необратимым. При обратимом кодировании на основе закодированного сообщения можно однозначно (без потери качества) восстановить кодируемое сообщение (исходный образ). Например, кодирование с помощью азбуки Морзе или штрихкода. При необратимом кодировании однозначное восстановление исходного образа невозможно. Например, кодирование аудиовизуальной информации (форматы jpg, mp3 или avi) или хеширование.
Различают общедоступные и секретные системы кодирования. Первые используются для облегчения информационного обмена, вторые – в целях сокрытия информации от посторонних лиц.
1 В некоторых секретных кодовых системах присутствуют элементы, позволяющие получать разные закодированные сообщения для определенного исходного сообщения (аддитивные числа, многозначные замены, правила перешифрования).
22.2. Общедоступные кодовые системы
Применение кодов нашло широкое применение в общественной жизни. Как отмечалось выше, даже сами знаки арифметических и логических операций – это кодовые обозначения. В частности, знак «+» для операции сложения (а также знак «-») придумали в немецкой математической школе «коссистов» (т.е. алгебраистов). Они используются в «Арифметике» Иоганна Видмана, изданной в 1489 г. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и» [17]. Если «копать еще глубже», то буква «А» — это кодовое обозначение для соответствующего звука.
В качестве других распространенных кодовых систем можно привести:
— обозначение химических элементов из периодической таблицы Дмитрия Ивановича Менделеева;
— сокращенные наименования дисциплин в расписании занятий студентов.
Ниже приводится описание других общедоступных кодовых систем в целях иллюстрации многообразия их назначения и способов представления кодовых обозначений [17].
Азбука Морзе — способ кодирования символов (букв алфавита, цифр, знаков препинания и др.) с помощью последовательности «точек» и «тире». За единицу времени принимается длительность одной точки. Длительность тире равна трём точкам. Пауза между элементами одного знака — одна точка (около 1/25 доли секунды), между знаками в слове — 3 точки, между словами — 7 точек. Назван в честь американского изобретателя и художника Сэмюэля Морзе.
| Русская буква | Латинская буква | Код Морзе | Русская буква | Латинская буква | Код Морзе | Символ | Код Морзе |
| A | A | · — | Р | R | · — · | 1 | · — — — — |
| Б | B | — · · · | С | S | · · · | 2 | · · — — — |
| В | W | · — — | Т | T | — | 3 | · · · — — |
| Г | G | — — · | У | U | · · — | 4 | · · · · — |
| Д | D | — · · | Ф | F | · · — · | 5 | · · · · · |
| Е (Ё) | E | · | Х | H | · · · · | 6 | — · · · · |
| Ж | V | · · · — | Ц | C | — · — · | 7 | — — · · · |
| З | Z | — — · · | Ч | O | — — — · | 8 | — — — · · |
| И | I | · · | Ш | CH | — — — — | 9 | — — — — · |
| Й | J | · — — — | Щ | Q | — — · — | 0 | — — — — — |
| К | K | — · — | Ъ | N | — — · — — | Точка | · · · · · · |
| Л | L | · — · · | Ы | Y | — · — — | Запятая | · — · — · — |
| М | M | — — | Ь (Ъ) | X | — · · — | — | · · — — · · |
| Н | N | — · | Э | E | · · — · · | ! | — — · · — — |
| О | O | — — — | Ю | U | · · — — | @ | · — — · — · |
| П | P | · — — · | Я | A | · — · — | Конец связи (end contact) | · · — · — |
Рис.22.1. Фрагмент азбуки Морзе
Изначально азбука Морзе применялась для передачи сообщений в телеграфе. При этом точки и тире передавались в виде электрических сигналов, проходящих по проводам. В настоящий момент азбуку Морзе, как правило, используют в местах, где другие средства обмена информации недоступны (например, в тюрьмах).
Любопытный факт связан с изобретателем первой лампочки Томасом Альвой Эдисоном (1847-1931 гг.). Он плохо слышал и общался со своей женой, Мэри Стиуэлл, с помощью азбуки Морзе. Во время ухаживания Эдисон сделал предложение, отстучав слова рукой, и она ответила тем же способом. Телеграфный код стал обычным средством общения для супругов. Даже когда они ходили в театр, Эдисон клал руку Мэри себе на колено, чтобы она могла «телеграфировать» ему диалоги актеров [44].
Код Бодо — цифровой 5-битный код. Был разработан Эмилем Бодо в 1870 г. для своего телеграфа. Код вводился прямо клавиатурой, состоящей из пяти клавиш, нажатие или ненажатие клавиши соответствовало передаче или непередаче одного бита в пятибитном коде. Существует несколько разновидностей (стандартов) данного кода (CCITT-1, CCITT-2, МТК-2 и др.) В частности МТК-2 представляет собой модификацию международного стандарта CCITT-2 с добавление букв кириллицы.
| Управляющие символы | ||||
| Двоичный код | Десятичный код | Назначение | ||
| 01000 | 8 | Возврат каретки | ||
| 00010 | 2 | Перевод строки | ||
| 11111 | 31 | Буквы латинские | ||
| 11011 | 27 | Цифры | ||
| 00100 | 4 | Пробел | ||
| 00000 | 0 | Буквы русские | ||
| Буквы, цифры и остальные символы | ||||
| Двоичный код | Десятичный код | Латинская буква | Русская буква | Цифры и прочие символы |
| 00011 | 3 | A | А | — |
| 11001 | 25 | B | Б | ? |
| 01110 | 14 | C | Ц | : |
| 01001 | 9 | D | Д | Кто там? |
| 00001 | 1 | E | Е | З |
| 01101 | 13 | F | Ф | Э |
| 11010 | 26 | G | Г | Ш |
| 10100 | 20 | H | Х | Щ |
| 00110 | 6 | I | И | 8 |
| 01011 | 11 | J | Й | Ю |
| 01111 | 15 | K | К | ( |
| 10010 | 18 | L | Л | ) |
| 11100 | 28 | M | М | . |
| 01100 | 12 | N | Н | , |
| 11000 | 24 | O | О | 9 |
| 10110 | 22 | P | П | 0 |
| 10111 | 23 | Q | Я | 1 |
| 01010 | 10 | R | Р | 4 |
| 00101 | 5 | S | С | ‘ |
| 10000 | 16 | T | Т | 5 |
| 00111 | 7 | U | У | 7 |
| 11110 | 30 | V | Ж | = |
| 10011 | 19 | W | В | 2 |
| 11101 | 29 | X | Ь | / |
| 10101 | 21 | Y | Ы | 6 |
| 10001 | 17 | Z | З | + |
Рис.22.2. Стандарт кода Бодо МТК-2
На следующем рисунке показана телетайпная перфолента с сообщением, переданным с помощью кода Бодо.
Рис. 22.3. Перфолента с кодом Бодо
Следует отметить два интересных факта, связанных с кодом Бодо.
1. Сотрудники телеграфной компании AT&T Гильберто Вернам и Мейджор Джозеф Моборн в 1917 г. предложили идею автоматического шифрования телеграфных сообщений на основе кода Бодо. Шифрование выполнялось методом гаммирования по модулю 2.
2. Соответствие между английским и русским алфавитами, принятое в МТК-2, было использовано при создании компьютерных кодировок КОИ-7 и КОИ-8.
ASCII и Unicode.
ASCII (англ. American Standard Code for Information Interchange) — американская стандартная кодировочная таблица для печатных и управляющих символов. Изначально была разработана как 7-битная для представления 128 символов, при использовании в компьютерах на символ выделялось 8 бит (1 байт), где 8-ой бит служил для контроля целостности (бит четности). Позднее, с задействованием 8 бита для представления дополнительных символов (всего 256 символов), например букв национальных алфавитов, стала восприниматься как половина 8-битной. В частности на основе ASCII были разработаны кодировки, содержащие буквы русского алфавита: для операционной системы MS-DOS — cp866 (англ. code page – кодовая страница), для операционной системы MS Windows – Windows 1251, для различных операционных систем – КОИ-8 (код обмена информацией, 8 битов), ISO 8859-5 и другие.
| Кодировка ASCII | Дополнительные символы | ||||||||||
| Двоичный код | Десятичный код | Символ | Двоичный код | Десятичный код | Символ | Двоичный код | Десятичный код | Символ | Двоичный код | Десятичный код | Символ |
| 00000000 | 0 | NUL | 01000000 | 64 | @ | 10000000 | 128 | Ђ | 11000000 | 192 | А |
| 00000001 | 1 | SOH | 01000001 | 65 | A | 10000001 | 129 | Ѓ | 11000001 | 193 | Б |
| 00000010 | 2 | STX | 01000010 | 66 | B | 10000010 | 130 | ‚ | 11000010 | 194 | В |
| 00000011 | 3 | ETX | 01000011 | 67 | C | 10000011 | 131 | ѓ | 11000011 | 195 | Г |
| 00000100 | 4 | EOT | 01000100 | 68 | D | 10000100 | 132 | „ | 11000100 | 196 | Д |
| 00000101 | 5 | ENQ | 01000101 | 69 | E | 10000101 | 133 | … | 11000101 | 197 | Е |
| 00000110 | 6 | ACK | 01000110 | 70 | F | 10000110 | 134 | † | 11000110 | 198 | Ж |
| 00000111 | 7 | BEL | 01000111 | 71 | G | 10000111 | 135 | ‡ | 11000111 | 199 | З |
| 00001000 | 8 | BS | 01001000 | 72 | H | 10001000 | 136 | € | 11001000 | 200 | И |
| 00001001 | 9 | HT | 01001001 | 73 | I | 10001001 | 137 | ‰ | 11001001 | 201 | Й |
| 00001010 | 10 | LF | 01001010 | 74 | J | 10001010 | 138 | Љ | 11001010 | 202 | К |
| 00001011 | 11 | VT | 01001011 | 75 | K | 10001011 | 139 | ‹ | 11001011 | 203 | Л |
| 00001100 | 12 | FF | 01001100 | 76 | L | 10001100 | 140 | Њ | 11001100 | 204 | М |
| 00001101 | 13 | CR | 01001101 | 77 | M | 10001101 | 141 | Ќ | 11001101 | 205 | Н |
| 00001110 | 14 | SO | 01001110 | 78 | N | 10001110 | 142 | Ћ | 11001110 | 206 | О |
| 00001111 | 15 | SI | 01001111 | 79 | O | 10001111 | 143 | Џ | 11001111 | 207 | П |
| 00010000 | 16 | DLE | 01010000 | 80 | P | 10010000 | 144 | ђ | 11010000 | 208 | Р |
| 00010001 | 17 | DC1 | 01010001 | 81 | Q | 10010001 | 145 | ‘ | 11010001 | 209 | С |
| 00010010 | 18 | DC2 | 01010010 | 82 | R | 10010010 | 146 | ’ | 11010010 | 210 | Т |
| 00010011 | 19 | DC3 | 01010011 | 83 | S | 10010011 | 147 | “ | 11010011 | 211 | У |
| 00010100 | 20 | DC4 | 01010100 | 84 | T | 10010100 | 148 | ” | 11010100 | 212 | Ф |
| 00010101 | 21 | NAK | 01010101 | 85 | U | 10010101 | 149 | • | 11010101 | 213 | Х |
| 00010110 | 22 | SYN | 01010110 | 86 | V | 10010110 | 150 | – | 11010110 | 214 | Ц |
| 00010111 | 23 | ETB | 01010111 | 87 | W | 10010111 | 151 | — | 11010111 | 215 | Ч |
| 00011000 | 24 | CAN | 01011000 | 88 | X | 10011000 | 152 | 11011000 | 216 | Ш | |
| 00011001 | 25 | EM | 01011001 | 89 | Y | 10011001 | 153 | ™ | 11011001 | 217 | Щ |
| 00011010 | 26 | SUB | 01011010 | 90 | Z | 10011010 | 154 | љ | 11011010 | 218 | Ъ |
| 00011011 | 27 | ESC | 01011011 | 91 | [ | 10011011 | 155 | › | 11011011 | 219 | Ы |
| 00011100 | 28 | FS | 01011100 | 92 | \ | 10011100 | 156 | њ | 11011100 | 220 | Ь |
| 00011101 | 29 | GS | 01011101 | 93 | ] | 10011101 | 157 | ќ | 11011101 | 221 | Э |
| 00011110 | 30 | RS | 01011110 | 94 | ^ | 10011110 | 158 | ћ | 11011110 | 222 | Ю |
| 00011111 | 31 | US | 01011111 | 95 | _ | 10011111 | 159 | џ | 11011111 | 223 | Я |
| 00100000 | 32 | 01100000 | 96 | ` | 10100000 | 160 | 11100000 | 224 | а | ||
| 00100001 | 33 | ! | 01100001 | 97 | a | 10100001 | 161 | Ў | 11100001 | 225 | б |
| 00100010 | 34 | « | 01100010 | 98 | b | 10100010 | 162 | ў | 11100010 | 226 | в |
| 00100011 | 35 | # | 01100011 | 99 | c | 10100011 | 163 | Ј | 11100011 | 227 | г |
| 00100100 | 36 | $ | 01100100 | 100 | d | 10100100 | 164 | ¤ | 11100100 | 228 | д |
| 00100101 | 37 | % | 01100101 | 101 | e | 10100101 | 165 | Ґ | 11100101 | 229 | е |
| 00100110 | 38 | & | 01100110 | 102 | f | 10100110 | 166 | ¦ | 11100110 | 230 | ж |
| 00100111 | 39 | ‘ | 01100111 | 103 | g | 10100111 | 167 | § | 11100111 | 231 | з |
| 00101000 | 40 | ( | 01101000 | 104 | h | 10101000 | 168 | Ё | 11101000 | 232 | и |
| 00101001 | 41 | ) | 01101001 | 105 | i | 10101001 | 169 | © | 11101001 | 233 | й |
| 00101010 | 42 | * | 01101010 | 106 | j | 10101010 | 170 | Є | 11101010 | 234 | к |
| 00101011 | 43 | + | 01101011 | 107 | k | 10101011 | 171 | « | 11101011 | 235 | л |
| 00101100 | 44 | , | 01101100 | 108 | l | 10101100 | 172 | ¬ | 11101100 | 236 | м |
| 00101101 | 45 | — | 01101101 | 109 | m | 10101101 | 173 | ¬ | 11101101 | 237 | н |
| 00101110 | 46 | . | 01101110 | 110 | n | 10101110 | 174 | ® | 11101110 | 238 | о |
| 00101111 | 47 | / | 01101111 | 111 | o | 10101111 | 175 | Ї | 11101111 | 239 | п |
| 00110000 | 48 | 0 | 01110000 | 112 | p | 10110000 | 176 | ° | 11110000 | 240 | р |
| 00110001 | 49 | 1 | 01110001 | 113 | q | 10110001 | 177 | ± | 11110001 | 241 | с |
| 00110010 | 50 | 2 | 01110010 | 114 | r | 10110010 | 178 | І | 11110010 | 242 | т |
| 00110011 | 51 | 3 | 01110011 | 115 | s | 10110011 | 179 | і | 11110011 | 243 | у |
| 00110100 | 52 | 4 | 01110100 | 116 | t | 10110100 | 180 | ґ | 11110100 | 244 | ф |
| 00110101 | 53 | 5 | 01110101 | 117 | u | 10110101 | 181 | µ | 11110101 | 245 | х |
| 00110110 | 54 | 6 | 01110110 | 118 | v | 10110110 | 182 | ¶ | 11110110 | 246 | ц |
| 00110111 | 55 | 7 | 01110111 | 119 | w | 10110111 | 183 | · | 11110111 | 247 | ч |
| 00111000 | 56 | 8 | 01111000 | 120 | x | 10111000 | 184 | ё | 11111000 | 248 | ш |
| 00111001 | 57 | 9 | 01111001 | 121 | y | 10111001 | 185 | № | 11111001 | 249 | щ |
| 00111010 | 58 | : | 01111010 | 122 | z | 10111010 | 186 | є | 11111010 | 250 | ъ |
| 00111011 | 59 | ; | 01111011 | 123 | < | 10111011 | 187 | » | 11111011 | 251 | ы |
| 00111100 | 60 | 01111110 | 126 | 10111110 | 190 | ѕ | 11111110 | 254 | ю | ||
| 00111111 | 63 | ? | 01111111 | 127 | DEL | 10111111 | 191 | ї | 11111111 | 255 | я |
Рис. 22.4. Кодовая страница Windows 1251
Unicode — стандарт кодирования символов, позволяющий представить знаки почти всех письменных языков. Стандарт был предложен в 1991 г. некоммерческой организацией «Консорциум Юникода» (англ. Unicode Consortium, Unicode Inc.). Применение этого стандарта позволяет закодировать большее число символов (чем в ASCII и прочих кодировках) за счет двухбайтового кодирования символов (всего 65536 символов). В документах Unicode могут соседствовать китайские иероглифы, математические символы, буквы греческого алфавита, латиницы и кириллицы.
Коды в стандарте Unicode разделены на несколько разделов. Первые 128 кодов соответствуют кодировке ASCII. Далее расположены разделы букв различных письменностей, знаки пунктуации и технические символы. В частности прописным и строчным буквам русского алфавита соответствуют коды 1025 (Ё), 1040-1103 (А-я) и 1105 (ё).
Шрифт Брайля — рельефно-точечный тактильный шрифт, предназначенный для письма и чтения незрячими людьми. Был разработан в 1824 г. французом Луи Брайлем (Louis Braille), сыном сапожника. Луи в возрасте трёх лет потерял зрение, в результате воспаления глаз, начавшегося от того, что мальчик поранился шорным ножом (подобие шила) в мастерской отца. В возрасте 15 лет он создал свой рельефно-точечный шрифт, вдохновившись простотой «ночного шрифта» капитана артиллерии Шарля Барбье (Charles Barbier), который использовался военными того времени для чтения донесений в темноте.
Для изображения символов (в основном букв и цифр) в шрифте Брайля используются 6 точек, расположенных в два столбца, по 3 в каждом.
Рис. 22.5. Нумерация точек
Каждому символу соответствует свой уникальный набор выпуклых точек. Таким образом, шрифт Брайля представляет собой систему для кодирования 2 6 = 64 символов. Но присутствие в шрифте управляющих символов (например, переход к буквам или цифрам) позволяет увеличить количество кодируемых символов.
| Управляющие символы | |||
| Символ шрифта Брайля | Назначение | ||
| ⠠ | Буквы | ||
| ⠼ | Цифры | ||
| Буквы, цифры и остальные символы | |||
| Символ шрифта Брайля | Латинские буквы | Русские буквы | Цифры |
| ⠁ | A | А | 1 |
| ⠃ | B | Б | 2 |
| ⠉ | C | Ц | 3 |
| ⠙ | D | Д | 4 |
| ⠑ | E | Е | 5 |
| ⠋ | F | Ф | 6 |
| ⠛ | G | Г | 7 |
| ⠓ | H | Х | 8 |
| ⠊ | I | И | 9 |
| ⠚ | J | Ж | 0 |
| ⠅ | K | К | |
| ⠇ | L | Л | |
| ⠍ | M | М | |
| ⠝ | N | Н | |
| ⠕ | O | О | |
| ⠏ | P | П | |
| ⠟ | Q | Ч | |
| ⠗ | R | Р | |
| ⠎ | S | С | |
| ⠞ | T | Т | |
| ⠥ | U | У | |
| ⠧ | V | ||
| ⠺ | W | В | |
| ⠭ | X | Щ | |
| ⠽ | Y | ||
| ⠵ | Z | З | |
| ⠡ | Ё | ||
| ⠯ | Й | ||
| ⠱ | Ш | ||
| ⠷ | Ъ | ||
| ⠮ | Ы | ||
| ⠾ | Ь | ||
| ⠪ | Э | ||
| ⠳ | Ю | ||
| ⠫ | Я | ||
| ⠲ | Точка | ||
| ⠂ | Запятая | ||
| ⠖ | Восклицательный знак | ||
| ⠢ | Вопросительный знак | ||
| ⠆ | Точка с запятой | ||
| ⠤ | Дефис | ||
| Пробел | |||
Рис. 22.6. Шрифт Брайля
Шрифт Брайля, в последнее время, стал широко применяться в общественной жизни и быту в связи с ростом внимания к людям с ограниченными возможностями.
Рис. 22.7. Надпись «Sochi 2014» шрифтом Брайля на золотой медали Параолимпийских игр 2014г.
Штрихкод — графическая информация, наносимая на поверхность, маркировку или упаковку изделий, представляющая собой последовательность черных и белых полос либо других геометрических фигур в целях ее считывания техническими средствами.
В 1948 г. Бернард Сильвер (Bernard Silver), аспирант Института Технологии Университета Дрекселя в Филадельфии, услышал, как президент местной продовольственной сети просил одного из деканов разработать систему, автоматически считывающую информацию о продукте при его контроле. Сильвер рассказал об этом друзьям — Норману Джозефу Вудланду (Norman Joseph Woodland) и Джордину Джохэнсону (Jordin Johanson). Втроем они начали исследовать различные системы маркировки. Их первая работающая система использовала ультрафиолетовые чернила, но они были довольно дороги, а кроме того, со временем выцветали.
Убежденный в том, что система реализуема, Вудланд покинул Филадельфию и перебрался во Флориду в квартиру своего отца для продолжения работы. 20 октября 1949 г. Вудланд и Сильвер подали заявку на изобретение, которая была удовлетворена 7 октября 1952 г. Вместо привычных нам линий патент содержал описание штрихкодовой системы в виде концентрических кругов.
Рис. 22.8. Патент системы Вудланда и Сильвера с концентрическими кругами, предшественниками современных штрихкодов
Впервые штрихкоды начали официально использоваться в 1974 г. в магазинах г. Трой, штат Огайо [44]. Системы штрихового кодирования нашли широкое применение в общественной жизни: торговля, почтовые отправления, финансовые и судебные уведомления, учет единиц хранения, идентификация личностей, контактная информация (веб-ссылки, адреса электронной почты, телефонные номера) и т.д.
Различают линейные (читаемые в одном направлении) и двумерные штрихкоды. Каждая из разновидностей различается как размерами графического изображения, так и объемами представленной информации. В следующей таблице приведены примеры некоторых разновидностей штрихкода.
Таблица 22.1. Разновидности штрихкодов
| Наименование | Пример штрих-кода | Примечания |
| Линейные | ||
| Universal Product Code, UPC (универсальный код товара) | (UPC-A) | Американский стандарт штрихкода, предназначенный для кодирования идентификатора товара и производителя. Имеются разновидности: — UPC-E – кодируются 8 цифр; — UPC-A – кодируется 13 цифр. |
| European Article Number, EAN (европейский номер товара) | (EAN-13) | Европейский стандарт штрихкода, предназначенный для кодирования идентификатора товара и производителя. Имеются разновидности: — EAN-8 – кодируются 8 цифр; — EAN 13 – кодируется 13 цифр; — EAN-128 – кодируется любое количество букв и цифр, объединенных в регламентированные группы. ГОСТ ИСО/МЭК 15420-2001 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики EAN/UPC (ЕАН/ЮПиСи)». |
| Code 128 (Код 128) | Включает в себя 107 символов, из которых 103 символа данных, 3 стартовых, и 1 остановочный символ. Для кодирования всех 128-ми символов ASCII предусмотрено три комплекта символов — A, B и C, которые могут использоваться внутри одного штрихкода. EAN-128 кодирует информацию по алфавиту Code 128. ГОСТ 30743-2001 (ИСО/МЭК 15417-2000) «Автоматическая идентификация. Кодирование штриховое. Спецификация символики Code 128 (Код 128)». | |
| Двумерные | ||
| DataMatrix (матричные данные) | Максимальное количество символов, которые помещаются в один код — 2048 байт. ГОСТ Р ИСО/МЭК 16022-2008 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики Data Matrix». | |
| QR-код (англ. quick response — быстрый отклик) | Квадраты в углах изображения позволяют нормализовать размер изображения и его ориентацию, а также угол, под которым сенсор относится к поверхности изображения. Точки переводятся в двоичные числа с проверкой контрольной суммы. Максимальное количество символов, которые помещаются в один QR-код: — цифры — 7089; — цифры и буквы (латиница) — 4296; — двоичный код — 2953 байт; — иероглифы — 1817. | |
| MaxiCode (максикод) | Размер — дюйм на дюйм (1 дюйм = 2.54 см). Используется для грузоотправительных и грузоприемных систем. Может вместить в себя столько же символов, что Code128. ГОСТ Р 51294.6-2000 «Автоматическая идентификация. Кодирование штриховое. Спецификация символики MaxiCode (Максикод)». | |
| PDF147 (англ. Portable Data File — переносимый файл данных) | Применяется при идентификации личности, учете товаров, при сдаче отчетности в контролирующие органы и других областях. Поддерживает кодирование до 2710 символов и может содержать до 90 строк. | |
| Microsoft Tag (метка Microsoft) | Разработан для распознавания при помощи фотокамер, встроенных в мобильные телефоны. Может вместить в себя столько же символов, что Code128. Предназначен для быстрой идентификации и получения на устройство заранее подготовленной информации (веб-ссылки, произвольного текста длиной до 1000 символов, телефонного номера и т.п.), привязанной к коду и хранящейся на сервере компании Microsoft. Содержит 13 байт плюс один дополнительный бит для контроля четности. | |
Представление чисел в двоичном виде (в компьютере). Как известно, информация, хранящаяся и обрабатываемая в компьютерах, представлена в двоичном виде. Бит (англ. binary digit — двоичное число; также игра слов: англ. bit — кусочек, частица) — единица измерения количества информации, равная одному разряду в двоичной системе счисления. С помощью бита можно закодировать (представить, различать) два состояния (0 или 1; да или нет). Увеличивая количество битов (разрядов), можно увеличить количество кодируемых состояний. Например, для байта (англ. byte), состоящего из 8 битов, количество кодируемых состояний составляет 2 8 = 256.
Числа кодируются в т.н. форматах с фиксированной и плавающей запятой.
1. Формат с фиксированной запятой, в основном, применяется для целых чисел, но может применяться и для вещественных чисел, у которых фиксировано количество десятичных знаков после запятой. Для целых чисел подразумевается, что «запятая» находится справа после младшего бита (разряда), т.е. вне разрядной сетки. В данном формате существуют два представления: беззнаковое (для неотрицательных чисел) и со знаком.
Для беззнакового представления все разряды отводятся под представление самого числа. Например, с помощью байта можно представить беззнаковые целые числа от 010 до 25510 (000000002 — 111111112) или вещественные числа с одним десятичным знаком от 0.010 до 25.510 (000000002 — 111111112). Для знакового представления, т.е. положительных и отрицательных чисел, старший разряд отводится под знак (0 – положительное число, 1 – отрицательное).
Различают прямой, обратный и дополнительный коды записи знаковых чисел.
В прямом коде запись положительного и отрицательного числа выполняется так же, как и в беззнаковом представление (за исключение того, что старший разряд отводится под знак). Таким образом, числа 510 и -510 записываются, как 000001012 и 100001012. В прямом коде имеются два кода числа 0: «положительный нуль» 000000002 и «отрицательный нуль» 100000002.
При использовании обратного кода отрицательное число записывается в виде инвертированного положительного числа (0 меняются на 1 и наоборот). Например, числа 510 и -510 записываются, как 000001012 и 111110102. Следует отметить, что в обратном коде, как и в прямом, имеются «положительный нуль» 000000002 и «отрицательный нуль» 111111112. Применение обратного кода позволяет вычесть одно число из другого, используя операцию сложения, т.е. вычитание двух чисел X – Y заменяется их суммой X + (-Y). При этом используются два дополнительных правила:
— вычитаемое число инвертируется (представляется в виде обратного кода);
— если количество разрядов результата получается больше, чем отведено на представление чисел, то крайний левый разряд (старший) отбрасывается, а к результату добавляется 12.
В следующей таблице приведены примеры вычитания.
Таблица 22.2. Примеры вычитания двух чисел с использованием обратного кода
| X – Y | 5 – 5 | 6 – 5 | 5 – 6 | 5 – (-6) |
| X2 | 00000101 | 00000110 | 00000101 | 00000101 |
| Y2 | 00000101 | 00000101 | 00000110 | 11111001 |
| Замена сложением | 5 + (-5) | 6 + (-5) | 5 + (-6) | 5 + 6 |
| Обратный код для вычитаемого (-Y2) | 11111010 | 11111010 | 11111001 | 00000110 |
| Сложение | 00000101 + 11111010 11111111 | 00000110 + 11111010 100000000 | 00000101 + 11111001 11111110 | 00000101 + 00000110 00001011 |
| Отбрасывание старшего разряда и добавление 12 | не требуется | 00000000 + 00000001 00000001 | не требуется | не требуется |
| Результат | -0 | 1 | -1 | 11 |
Несмотря на то, что обратный код значительно упрощает вычислительные процедуры, а соответственно и быстродействие компьютеров, наличие двух «нулей» и другие условности привели к появлению дополнительного кода. При представлении отрицательного числа его модуль вначале инвертируется, как в обратном коде, а затем к инверсии сразу добавляется 12.
В следующей таблице приведены некоторые числа в различном кодовом представлении.
Таблица 22.3. Представление чисел в различных кодах
| Десятичное представление | Код двоичного представления (8 бит) | ||
| прямой | обратный | дополнительный | |
| 127 | 01111111 | 01111111 | 01111111 |
| 6 | 00000110 | 00000110 | 00000110 |
| 5 | 00000101 | 00000101 | 00000101 |
| 1 | 00000001 | 00000001 | 00000001 |
| 0 | 00000000 | 00000000 | 00000000 |
| -0 | 10000000 | 11111111 | — |
| -1 | 10000001 | 11111110 | 11111111 |
| -5 | 10000101 | 11111010 | 11111011 |
| -6 | 10000110 | 11111001 | 11111010 |
| -127 | 11111111 | 10000000 | 10000001 |
| -128 | — | — | 10000000 |
При представлении отрицательных чисел в дополнительных кодах второе правило несколько упрощается — если количество разрядов результата получается больше, чем отведено на представление чисел, то только отбрасывается крайний левый разряд (старший).
Таблица 22.4. Примеры вычитания двух чисел с использованием дополнительного кода
| X – Y | 5 – 5 | 6 – 5 | 5 – 6 | 5 – (-6) |
| X2 | 00000101 | 00000110 | 00000101 | 00000101 |
| Y2 | 00000101 | 00000101 | 00000110 | 11111010 |
| Замена сложением | 5 + (-5) | 6 + (-5) | 5 + (-6) | 5 + 6 |
| Дополнительный код для вычитаемого (-Y2) | 11111011 | 11111011 | 11111010 | 00000110 |
| Сложение | 00000101 + 11111011 00000000 | 00000110 + 11111011 100000001 | 00000101 + 11111010 11111111 | 00000101 + 00000110 00001011 |
| Отбрасывание старшего разряда и добавление 12 | не требуется | 00000001 | не требуется | не требуется |
| Результат | -0 | 1 | -1 | 11 |
Можно возразить, что представление чисел в дополнительных кодах требует на одну операцию больше (после инверсии всегда требуется сложение с 12), что может и не потребоваться в дальнейшем, как в примерах с обратными кодами. В данном случае срабатывает известный «принцип чайника». Лучше сделать процедуру линейной, чем применять в ней правила «Если A то B» (даже если оно одно). То, что с человеческой точки зрения кажется увеличением трудозатрат (вычислительной и временной сложности), с точки зрения программно-технической реализации может оказаться эффективней.
Еще одно из преимуществ дополнительного кода перед обратным заключается в возможности представления в единице информации на одно число (состояние) больше, за счет исключения «отрицательного нуля». Поэтому, как правило, диапазон представления (хранения) для знаковых целых чисел длиной один байт составляет от +127 до -128.
2. Формат с плавающей запятой, в основном, используется для вещественных чисел. Число в данном формате представляется в экспоненциальном виде
где e — основание показательной функции;
n — порядок основания;
e n — характеристика числа;
m — мантисса (лат. mantissa — прибавка) – множитель, на который надо умножить характеристику числа, чтобы получить само число.
Например, число десятичное число 350 может быть записано, как 3.5 * 10 2 , 35 * 10 1 , 350 * 10 0 и т.д. В нормализованной научной записи, порядок n выбирается такой, чтобы абсолютная величина m оставалась не меньше единицы, но строго меньше десяти (1 ≤ |m| 2 . При отображении чисел в программах, учитывая, что основание равно 10, их записывают в виде m E ± n, где Е означает «*10^» («…умножить на десять в степени…»). Например, число 350 – 3.5Е+2, а число 0.035 – 3.5Е-2.
Так как числа хранится и обрабатывается в компьютерах в двоичном виде, то для этих целей принимается e = 2. Одной из возможных форм двоичного представления чисел с плавающей запятой является следующая.
| bn± | bn7 | bn6 | bn5 | bn4 | bn3 | bn2 | bn1 | bm± | bm15 | bm14 | bm13 | bm12 | bm11 | bm10 | bm9 | bm8 | bm7 | bm6 | bm5 | bm4 | bm3 | bm2 | bm1 |
| знак | величина | знак | величина | ||||||||||||||||||||
| порядок | мантисса | ||||||||||||||||||||||
Рис. 22.9. Двоичный формат представления чисел с плавающей запятой
Биты bn± и bm±, означающие знак порядка и мантиссы, кодируются аналогично числам с фиксированной запятой: для положительных чисел «0», для отрицательных – «1». Значение порядка выбирается таким образом, чтобы величина целой части мантиссы в десятичном (и соответственно в двоичном) представлении равнялась «1», что будет соответствовать нормализованной записи для двоичных чисел. Например, для числа 35010 порядок n = 810 = 0010002 (350 = 1.3671875 * 2 8 ), а для 57610 – n = 910 = 0010012 (576 = 1.125 * 2 9 ). Битовое представление величины порядка может быть выполнено в прямом, обратном или дополнительном коде (например, для n = 810 бинарный вид 0010002). Величина мантиссы отображает дробную часть. Для ее преобразования в двоичный вид, она последовательно умножается на 2, пока не станет равной 0. Например,
Рис. 22.10. Пример получения дробной части в бинарном виде
Целые части, получаемые в результате последовательного перемножения, и представляют собой двоичный вид дробной части (0.367187510 = 01011112). Оставшаяся часть разрядов величины мантиссы заполняется 0. Таким образом, итоговый вид числа 350 в формате с плавающей запятой с учетом представления мантиссы в нормализованной записи
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| знак + | величина 2 8 | знак + | величина (1) + 0.3671875 | ||||||||||||||||||||
| порядок | мантисса | ||||||||||||||||||||||
Рис. 22.11. Двоичный вид числа 350
В программно-аппаратных реализациях арифметических действий широко распространен стандарт представления чисел с плавающей точкой IEEE 2 754 (последняя редакция «754-2008 — IEEE Standard for Floating-Point Arithmetic»). Данный стандарт определяет форматы с плавающими запятыми для представления чисел одинарной (англ. single, float) и двойной (англ. double) точности. Общая структура форматов
| bn± | bni | . | bn1 | bmj | . | bm1 |
| знак мантиссы | порядок | величина мантиссы | ||||
Рис. 22.12. Общий формат представления двоичных чисел в стандарте IEEE 754
Форматы представления отличаются количеством бит (байт), отводимым для представления чисел, и, соответственно, точностью представления самих чисел.
Таблица 22.5. Характеристики форматов представления двоичных чисел в стандарте IEEE 754
| Формат | single | double |
| Общий размер, бит (байт) | 32 (4) | 64 (8) |
| Число бит для порядка | 8 | 11 |
| Число бит для мантиссы (без учета знакового бита) | 23 | 52 |
| Величина порядка | 2 128 .. 2 -127 (±3.4 * 10 38 .. 1.7 * 10 -38 ) | 2 1024 .. 2 -1023 (±1.8 * 10 308 .. 9.0 * 10 -307 ) |
| Смещение порядка | 127 | 1023 |
| Диапазон представления чисел (без учета знака) | ±1.4 * 10 -45 .. 3.4 * 10 38 | ±4.9 * 10 -324 .. 1.8 * 10 308 |
| Количество значащих цифр числа (не более) | 8 | 16 |
Особенностью представления чисел по стандарту IEEE является отсутствие бита под знак порядка. Несмотря на это, величина порядка может принимать как положительные значения, так и отрицательные. Этот момент учитывается т.н. «смещением порядка». После преобразования двоичного вида порядка (записанного в прямом коде) в десятичный от полученной величины отнимается «смещение порядка». В результате получается «истинное» значения порядка числа. Например, если для числа одинарной точности указан порядок 111111112 (= 25510), то величина порядка на самом деле 12810 (= 25510 — 12710), а если 000000002 (= 010), то -12710 (= 010 — 12710).
Величина мантиссы указывается, как и в предыдущем случае, в нормализованном виде.
C учетом вышеизложенного, число 35010 в формате одинарной точности стандарта IEEE 754 записывается следующим образом.
| 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| знак мантиссы + | порядок 2 8 (8 = 135 — 127) | величина мантиссы (1) + 0.3671875 | |||||||||||||||||||||||||||||
Рис. 22.13. Двоичный вид числа 350 по стандарту IEEE
К другим особенностям стандарта IEEE относится возможность представления специальных чисел. К ним относятся значения NaN (англ. Not a Number — не число) и +/-INF (англ. Infinity — бесконечность), получающихся в результате операций типа деления на ноль. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы.
В заключение по числам с плавающей запятой несколько слов о пресловутой «ошибке округления». Т.к. в двоичной форме представления числа хранится только несколько значащих цифр, она не может «покрыть» все многообразие вещественных чисел в заданном диапазоне. В результате, если число невозможно точно представить в двоичной форме, оно представляется ближайшим возможным. Например, если к числу типа double «0.0» последовательно добавлять «1.7», то можно обнаружить следующую «картину» изменения значений.
0.0
1.7
3.4
5.1
6.8
8.5
10.2
11.899999999999999
13.599999999999998
15.299999999999997
16.999999999999996
18.699999999999996
20.399999999999995
22.099999999999994
23.799999999999994
25.499999999999993
27.199999999999992
28.89999999999999
30.59999999999999
32.29999999999999
33.99999999999999
35.699999999999996
37.4
39.1
40.800000000000004
42.50000000000001
44.20000000000001
45.90000000000001
47.600000000000016
…
Рис. 22.14. Результат последовательного добавления числа 1.7 (Java 7)
Другой нюанс обнаруживается при сложении двух чисел, у которых значительно отличается порядок. Например, результатом сложения 10 10 + 10 -10 будет 10 10 . Даже если последовательно триллион (10 12 ) раз добавлять 10 -10 к 10 10 , то результат останется прежним 10 10 . Если же к 10 10 добавить произведение 10 -10 * 10 12 , что с математической точки зрения одно и то же, результат станет 10000000100 (1.0000000100 * 10 10 ).
Генетический код — свойственная всем живым организмам кодированная аминокислотная последовательность белков. Кодирование выполняется при помощи нуклеотидов 3 , входящих в состав ДНК (дезоксирибонуклеиновой кислоты). ДКН — макромолекула, обеспечивающая хранение, передачу из поколения в поколение и реализацию генетической программы развития и функционирования живых организмов. Пожалуй, самый главный код в истории человечества.
В ДНК используется четыре азотистых основания — аденин (А), гуанин (G), цитозин (С), тимин (T), которые в русскоязычной литературе обозначаются буквами А, Г, Ц и Т. Эти буквы составляют алфавит генетического кода. В молекулах ДНК нуклеотиды выстраиваются в цепочки и, таким образом, получаются последовательности генетических букв.
Белки практически всех живых организмов построены из аминокислот всего 20 видов. Эти аминокислоты называют каноническими. Каждый белок представляет собой цепочку или несколько цепочек аминокислот, соединенных в строго определенной последовательности. Эта последовательность определяет строение белка, а, следовательно, все его биологические свойства. Синтез белков (т.е. реализация генетической информации в живых клетках) осуществляется на основе информации, заложенной в ДНК. Для кодирования каждой из 20 аминокислот, а также сигнала «стоп», означающего конец белковой последовательности, достаточно трех последовательных нуклеотидов (триплета).
Рис. 22.15. Фрагмент ДНК
2 IEEE (англ. Institute of Electrical and Electronics Engineers) — институт инженеров по электротехнике и электронике.
3 Содержит азотистое основание, соединенное с сахаром, и фосфорную кислоту.
22.3. Секретные кодовые системы
Секретные коды, как и шифры, предназначены для обеспечения конфиденциальности информации. Изначально секретные кодовые системы представляли собой стеганографическую систему, в основе которой лежало подобие жаргонного кода. Они возникли в целях сокрытия имен реальных людей, упоминавшихся в переписке. Это были небольшие списки, в которых в были записаны скрываемые имена, а напротив них — кодовые замены (подстановки). Официальные коды для сокрытия содержания донесений, которыми пользовались папские эмиссары и послы средиземноморских городов-государств, найденные в ранних архивах Ватикана, датируются XIV в. По мере возрастания потребности в безопасности переписки, у представителей городов-государств появились более обширные перечни, которые включали в себя не только кодовые замены имен людей, но и стран, городов, видов оружия, провианта и т.д. В целях повышения защищенности информации к перечням были добавлены шифралфавиты для кодирования слов, не вошедших в перечень, а также правила их использования, базирующиеся на различных стеганографических и криптографических методах. Такие сборники получили название «номенклаторы». С XV и до середины XIX в. они были основной формой обеспечения конфиденциальности информации [43].
Вплоть до XVII столетия в номенклаторах слова открытого текста и их кодовые замены шли в алфавитном порядке, пока французский криптолог Антуан Россиньоль не предложил использовать более стойкие номенклаторы, состоящие из двух частей. В них существовало два раздела: в одном перечислялись в алфавитном порядке элементы открытого текста, а кодовые элементы были перемешаны. Во второй части в алфавитном порядке шли перечни кодов, а перемешанными были уже элементы открытого текста.
Изобретение телеграфа и азбуки Морзе, а также прокладка трансатлантического кабеля в середине XIX в. значительно расширило сферы применения секретных кодов. Помимо традиционных областей их использования (в дипломатической переписке и в военных целях) они стали широко использоваться в коммерции и на транспорте. Секретные кодовые системы того времени в своем названии содержали слово «код» («Код Госдепартамента (1867 г.)», «Американский код для окопов», «Речные коды : Потомак», «Черный код») или «шифр» («Шифр Госдепартамента (1876 г.)», «Зеленый шифр»). Следует отметить, что, несмотря на наличие в названии слова «шифр», в основу этих систем было положено кодирование.
Рис. 22.16. Фрагмент «Шифра Госдепартамента (1899 г.)»
Разработчики кодов, как и составители шифров, нередко добавляли дополнительные степени защиты, чтобы затруднить взлом своих кодов. Такой процесс называется перешифрованием. В итоге секретные кодовые системы сочетали в себе, как стеганографические, так и криптографические способы обеспечения конфиденциальности информации. Наиболее популярные из них приведены в следующей таблице.
Таблица 22.6. Способы обеспечения конфиденциальности информации в секретных кодовых системах
| Способ | Тип | Примечания | Примеры (кодируемое слово – кодовое обозначение) |
| Замена слова (словосочетания) другим словом произвольной длины | стеганографический | Аналог — жаргонный код. Для одного кодируемого слова могли использоваться несколько кодовых обозначений. | 1. Номенклатор города Сиены (XV в.): Cardinales (кардинал) – Florenus; Antonello da Furli (Антолло да Фурли) – Forte. |
2. Шифр Госдепартамента 1899 г.: Russia (Россия) – Promotes; Cabinet of Russia (Правительство России) – Promptings.
3. Код руководителя службы связи (1871 г.): 10:30 – Anna, Ida; 13th (тринадцатый) – Charles, Mason.
2. Код Госдепартамента А-1 (1919 г.): Diplomat (дипломат) – BUJOH; Diplomatic corps (дипломатический корпус) – BEDAC.
Для одного кодируемого слова могли использоваться несколько кодовых обозначений.
2. Код вещания для торговых судов союзников во Второй мировой войне (BAMS): остров – 36979; порт – 985.
2. Американский служебный радиокод № 1 (1918 г.): Oil (масло) – 001; Bad (плохой) – 642.
В качестве кодового обозначения могли использоваться буквы, числа, графические обозначения.
Применялась для слов, отсутствующих в списке кодируемых.
2. Номенклатор Джеймса Мэдисона (1781 г.): o – 527; p – 941.
3. Американский код для окопов (1918 г.): a – 1332 .. 2795 или CEW .. ZYR. Содержал также 30 алфавитов шифрозамен для перешифрования кодовых обозначений.
В качестве кодового обозначения могли использоваться буквы, числа, графические обозначения.
2. Номенклатор X-Y-Z (1737 г.): ce – 493; ab – 1194.
Ничего назначавшие (лат. nihil importantes) символы использовались для запутывания криптоаналитиков.
2. Речные коды : Потомак (1918 г.): ASY.
Аддитивное число, добавляемое к числовому кодовому обозначению, служило в качестве переменной части кода (ключа).
Сочетание различных способов кодирования и перешифровки в кодовой системе было обычной практикой у разработчиков кодов и стало применяться практически с самого начала их появления. Так, еще в номенклаторе, использовавшемся в г. Сиена в XV в., помимо кодовых замен слов, применялись шифралфавиты для замены букв, их удвоенных сочетаний и пустых знаков. Наибольшего расцвета эта практика получила в конце XIX – начале XX вв. В частности в «Шифре Госдепартамента 1876 г.» (англ. Red Book – Красная книга), состоящем из 1200 страниц, и его дополнении «Неподдающийся декодированию код: дополнение к шифру Госдепартамента» применялись:
— кодовые обозначения в виде слов и чисел;
— 30 шифралфавитов для замены букв;
— 50 правил перешифрования, включая аддитивные числа, перестановки кодовых обозначений и их частей.
В дополнении к «Шифру Госдепартамента 1899 г.» (англ. Blue Book – Синяя книга) были описаны еще 25 дополнительных правил перешифрования: изменение направления чтения и записи, прибавление или вычитание чисел, замена кодовых чисел другими кодовыми числами.
Разработчики кодов, чтобы закодировать сообщение, могут не только создавать с самого начала новые коды, но и воспользоваться уже имеющимися текстами. Т.н. книжные коды по своей сути аналогичны книжному шифру. В отличие от них замене подлежит не буква, а все слово целиком. Таким образом, кодовая замена представляет собой тройку чисел «страница.строка.слово». В книжных шифрах, как и в кодовых системах, рассмотренных выше, нашли широкое применение различные способы перешифровки. В частности, аддитивные числа, перестановки цифр и повторные замены.
Несомненным преимуществом книжного кода является то, что исключается необходимость использовать вызывающие подозрение кодовые книги — обнаружение таковой может привести к провалу агента. В то же время саму книгу можно потерять или ее могут украсть, в результате чего окажется скомпрометированной вся система.
Источник