Код хаффмана табличный способ

Коды Фано и Хаффмана являются оптимальными и префиксными. При построении искомых кодов будем применять как традиционный табличный способ кодирования, так и использовать «кодовые деревья».

При кодировании по Фано все сообщения записываются в таблицу по степени убывания вероятности и разбиваются на две группы примерно (насколько это возможно) равной вероятности. Соответственно этой процедуре из корня кодового дерева исходят два ребра, которым в качестве весов присваиваются полученные вероятности. Двум образовавшимся вершинам приписывают кодовые символы 0 и 1. Затем каждая из групп вероятностей вновь делится на две подгруппы примерно равной вероятности. В соответствии с этим из каждой вершины 0 и 1 исходят по два ребра с весами, равными вероятностям подгрупп, а вновь образованным вершинам приписывают символы 00 и 01, 10 и 11. В результате многократного повторения процедуры разделения вероятностей и образования вершин приходим к ситуации, когда в качестве веса, приписанного ребру бинарного дерева, выступает вероятность одного из данных сообщений. В этом случае вновь образованная вершина оказывается листом дерева, т.к. процесс деления вероятностей для нее завершен. Задача кодирования считается решенной, когда на всех ветвях кодового бинарного дерева образуются листья.

Пример 151. Закодировать по Фано сообщения, имеющие следующие вероятности:

сообщение	1	2	3	4	5	6	7
вероятность	0,4	0,2	0,1	0,1	0,1	0,05	0,05

Решение 1 (с использованием кодового дерева)

Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами.

Решение 2 (табличный способ)

Цена кодирования (средняя длина кодового слова является критерием степени оптимальности кодирования. Вычислим ее в нашем случае.

Для того, чтобы закодировать сообщения по Хаффману, предварительно преобразуется таблица, задающая вероятности сообщений. Исходные данные записываются в столбец, две последние (наименьшие) вероятности в котором складываются, а полученная сумма становится новым элементом таблицы, занимающим соответствующее место в списке убывающих по величине вероятностей. Эта процедура продолжается до тех пор, пока в столбце не останутся всего два элемента.

Пример 152. Закодировать сообщения из предыдущего примера по методу Хаффмана.

Решение 1. Первый шаг

Вторым шагом производим кодирование, «проходя» по таблице справа налево (обычно это проделывается в одной таблице):

Решение 2. Построение кодового дерева начинается с корня. Двум исходящим из него ребрам приписывается в качестве весов вероятности 0,6 и 0,4, стоящие в последнем столбце. Образовавшимся при этом вершинам дерева приписываются кодовые символы 0 и 1. Далее «идем» по таблице справа налево. Поскольку вероятность 0,6 является результатом сложения двух вероятностей 0,4 и 0,2, из вершины 0 исходят два ребра с весами 0,4 и 0,2 соответственно, что приводит к образованию двух новых вершин с кодовыми символами 00 и 01. Процедура продолжается до тех пор, пока в таблице остаются вероятности, получившиеся в результате суммирования. Построение кодового дерева заканчивается образованием семи листьев, соответствующих данным сообщениям с присвоенными им кодами. Дерево, полученное в результате кодирования по Хаффману, имеет следующий вид:

Листья кодового дерева представляют собой кодируемые сообщения с присвоенными им кодовыми словами. Таблица кодов имеет вид:

сообщение	1	2	3	4	5	6	7
код	1	01	0010	0011	0000	00010	00011

Цена кодирования здесь будет равна

Для передачи данных сообщений можно перейти от побуквенного (поцифрового) кодирования к кодированию «блоков», состоящих из фиксированного числа последовательных «букв».

Пример 153. Провести кодирование по методу Фано двухбуквенных комбинаций, когда алфавит состоит из двух букв и , имеющих вероятности = 0,8 и = 0,2.

Цена кода , и на одну букву алфавита приходится 0,78 бита информации. При побуквенном кодировании на каждую букву приходится следующее количество информации:

Пример 154. Провести кодирование по Хаффману трехбуквенных комбинаций для алфавита из предыдущего примера.

Построим кодовое дерево.

Найдем цену кодирования

На каждую букву алфавита приходится в среднем 0,728 бита, в то время как при побуквенном кодировании — 0,72 бита.

Большей оптимизации кодирования можно достичь еще и использованием трех символов — 0, 1, 2 — вместо двух. Тринарное дерево Хаффмана получается, если суммируются не две наименьшие вероятности, а три, и приписываются каждому левому ребру 0, правому — 2, а серединному — 1.

Пример 155. Построить тринарное дерево Хаффмана для кодирования трехбуквенных комбинаций из примера 153 .

Решение. Составим таблицу тройного «сжатия» по методу Хаффмана

Тогда тринарное дерево выглядит следующим образом:

Вопросы для самоконтроля

1. Как определяется среднее число элементарных сигналов, приходящихся на одну букву алфавита?

2. Префиксные коды.

3. Сколько требуется двоичных знаков для записи кодированного сообщения?

4. На чем основано построение кода Фано?

5. Что такое сжатие алфавита?

6. Какой код самый выгодный?

7. Основная теорема о кодировании.

8. Энтропия конкретных типов сообщений.

I 301. Проведите кодирование по методу Фано алфавита из четырех букв, вероятности которых равны 0,4; 0,3; 0,2 и 0,1.

302. Алфавит содержит 7 букв, которые встречаются с вероятностями 0,4; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05. Осуществите кодирование по методу Фано.

303. Алфавит состоит из двух букв, и , встречающихся с вероятностями = 0,8 и = 0,2. Примените метод Фано к кодированию всевозмож-ных двухбуквенных и трехбуквенных комбинаций.

304. Проведите кодирование по методу Хаффмана трехбуквенных слов из предыдущей задачи.

305. Проведите кодирование 7 букв из задачи 302 по методу Хаффмана.

306. Проведите кодирование по методам Фано и Хаффмана пяти букв, равновероятно встречающихся.

II 307. Осуществите кодирование двухбуквенных комбинаций четырех букв из задачи 301.

308. Проведите кодирование всевозможных четырехбуквенных слов из задачи 303.

III 309. Сравните эффективность кодов Фано и Хаффмана при кодировании алфавита из десяти букв, которые встречаются с вероятностями 0,3; 0,2; 0,1; 0,1; 0,1; 0,05; 0,05; 0,04; 0,03; 0,03.

310. Сравните эффективность двоичного кода Фано и кода Хаффмана при кодировании алфавита из 16 букв, которые встречаются с вероятностями 0,25; 0,2; 0,1; 0,1; 0,05; 0,04; 0,04; 0,04; 0,03; 0,03; 0,03; 0,03; 0,02; 0,02; 0,01; 0,01.

Источник

Алгоритм Хаффмана

Алгоритм Хаффмана (англ. Huffman’s algorithm) — алгоритм оптимального префиксного кодирования алфавита. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. Используется во многих программах сжатия данных, например, PKZIP 2, LZH и др.

Содержание

Определение [ править ]

Определение:

Пусть [math]A=\,a_<2>, \ldots ,a_\>[/math] — алфавит из [math]n[/math] различных символов, [math]W=\,w_<2>, \ldots ,w_\>[/math] — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов [math]C=\,c_<2>, \ldots ,c_\>[/math] , где [math]c_[/math] является кодом для символа [math]a_[/math] , такой, что:

[math]c_[/math] не является префиксом для [math]c_[/math] , при [math]i \ne j[/math] ,

cумма [math]\sum\limits_ w_\cdot |c_|[/math] минимальна ( [math]|c_|[/math] — длина кода [math]c_[/math] ),

называется кодом Хаффмана.

Алгоритм построения бинарного кода Хаффмана [ править ]

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
Из списка выберем два узла с наименьшим весом.
Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
Добавим к списку только что сформированный узел вместо двух объединенных узлов.
Если в списке больше одного узла, то повторим пункты со второго по пятый.

Время работы [ править ]

Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время [math]O(N \log N)[/math] .Такую асимптотику можно улучшить до [math]O(N)[/math] , используя обычные массивы.

Пример [ править ]

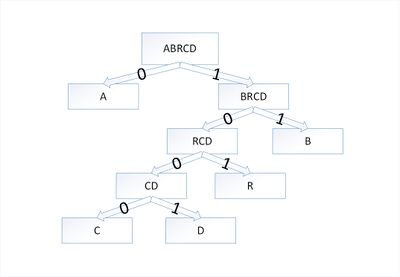
Закодируем слово [math]abracadabra[/math] . Тогда алфавит будет [math]A= \ [/math] , а набор весов (частота появления символов алфавита в кодируемом слове) [math]W=\<5, 2, 2, 1, 1\>[/math] :

В дереве Хаффмана будет [math]5[/math] узлов:

Узел	a	b	r	с	d
Вес	5	2	2	1	1

По алгоритму возьмем два символа с наименьшей частотой — это [math]c[/math] и [math]d[/math] . Сформируем из них новый узел [math]cd[/math] весом [math]2[/math] и добавим его к списку узлов:

Узел	a	b	r	cd
Вес	5	2	2	2

Затем опять объединим в один узел два минимальных по весу узла — [math]r[/math] и [math]cd[/math] :

Узел	a	rcd	b
Вес	5	4	2

Еще раз повторим эту же операцию, но для узлов [math]rcd[/math] и [math]b[/math] :

Узел	brcd	a
Вес	6	5

На последнем шаге объединим два узла — [math]brcd[/math] и [math]a[/math] :

Узел	abrcd
Вес	11

Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):

Символ	a	b	r	с	d
Код	0	11	101	1000	1001

Таким образом, закодированное слово [math]abracadabra[/math] будет выглядеть как [math]01110101000010010111010[/math] . Длина закодированного слова — [math]23[/math] бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы [math]33[/math] бита, что существенно больше.

Корректность алгоритма Хаффмана [ править ]

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. В сформулированной ниже лемме показано соблюдение свойства жадного выбора.

Доказательство: [math]\triangleright[/math]

Возьмем дерево [math]T[/math] , представляющее произвольный оптимальный префиксный код для алфавита [math]C[/math] . Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] — листья с общим родительским узлом, находящиеся на максимальной глубине.

Пусть символы [math]a[/math] и [math]b[/math] имеют общий родительский узел и находятся на максимальной глубине дерева [math]T[/math] . Предположим, что [math]f[a] \leqslant f[b][/math] и [math]f[x] \leqslant f[y][/math] . Так как [math]f[x][/math] и [math]f[y][/math] — две наименьшие частоты, а [math]f[a][/math] и [math]f[b][/math] — две произвольные частоты, то выполняются отношения [math]f[x] \leqslant f[a][/math] и [math]f[y] \leqslant f[b][/math] . Пусть дерево [math]T'[/math] — дерево, полученное из [math]T[/math] путем перестановки листьев [math]a[/math] и [math]x[/math] , а дерево [math]T»[/math] — дерево полученное из [math]T'[/math] перестановкой листьев [math]b[/math] и [math]y[/math] . Разность стоимостей деревьев [math]T[/math] и [math]T'[/math] равна:

[math]B(T) — B(T’) = \sum\limits_ f(c)d_T(c) — \sum\limits_ f(c)d_(c) = (f[a] — f[x])(d_T(a) — d_T(x)),[/math]

что больше либо равно [math]0[/math] , так как величины [math]f[a] — f[x][/math] и [math]d_T(a) — d_T(x)[/math] неотрицательны. Величина [math]f[a] — f[x][/math] неотрицательна, потому что [math]x[/math] — лист с минимальной частотой, а величина [math]d_T(a) — d_T(x)[/math] является неотрицательной, так как лист [math]a[/math] находится на максимальной глубине в дереве [math]T[/math] . Точно так же перестановка листьев [math]y[/math] и [math]b[/math] не будет приводить к увеличению стоимости. Таким образом, разность [math]B(T’) — B(T»)[/math] тоже будет неотрицательной.

Таким образом, выполняется неравенство [math]B(T») \leqslant B(T)[/math] . С другой стороны, [math]T[/math] — оптимальное дерево, поэтому должно выполняться неравенство [math]B(T) \leqslant B(T»)[/math] . Отсюда следует, что [math]B(T) = B(T»)[/math] . Значит, [math]T»[/math] — дерево, представляющее оптимальный префиксный код, в котором символы [math]x[/math] и [math]y[/math] имеют одинаковую максимальную длину, что и доказывает лемму. [math]\triangleleft[/math]

Лемма (2):

Доказательство:

[math]\triangleright[/math]

Сначала покажем, что стоимость [math]B(T)[/math] дерева [math]T[/math] может быть выражена через стоимость [math]B(T’)[/math] дерева [math]T'[/math] . Для каждого символа [math]c \in C \backslash \[/math] верно [math]d_T(C) = d_[/math] , значит, [math]f[c]d_T(c) = f[c]d_(c)[/math] . Так как [math]d_T(x) = d_T(y) = d_ (z) + 1[/math] , то

[math]f[x]d_T(x) + f[y]d_T(y) = (f[x] + f[y])(d_(z) + 1) = f[z]d_(z) + (f[x] + f[y])[/math]

из чего следует, что

[math] B(T) = B(T’) + f[x] + f[y] [/math]

[math] B(T’) = B(T) — f[x] — f[y] [/math]

Докажем лемму от противного. Предположим, что дерево [math]T[/math] не представляет оптимальный префиксный код для алфавита [math]C[/math] . Тогда существует дерево [math]T»[/math] такое, что [math]B(T») \lt B(T)[/math] . Согласно лемме (1), элементы [math]x[/math] и [math]y[/math] можно считать дочерними элементами одного узла. Пусть дерево [math]T»'[/math] получено из дерева [math]T»[/math] заменой элементов [math]x[/math] и [math]y[/math] листом [math]z[/math] с частотой [math]f[z] = f[x] + f[y][/math] . Тогда

[math]B(T»’) = B(T») — f[x] — f[y] \lt B(T) — f[x] — f[y] = B(T’)[/math] ,

Источник