Классы точности средств измерения способы увеличения точности измерения поверка средств измерений

Что нужно знать о классе точности измерительного прибора?

Измерительные приборы: вольтметры, амперметры, токовые клещи, осциллографы и другие — это устройства, предназначенные для определения искомых величин в заданном диапазоне, каждый из них имеет свою точность, причем устройства, измеряющие одну и ту же величину, в зависимости от модели, могут отличаться по точности и классу.

В каких-то ситуациях достаточно просто определить значение, например, вольтаж батарейки, а в других необходимо выполнить многократное повторение измерений высокоточными приборами для получения максимально достоверного результата, так в чем отличие таких измерительных устройств, что означает класс точности, сколько их бывает, как его определить и многое другое читайте далее в нашей статье.

Что такое класс точности

Определение: «Класс точности измерения — это общая характеристика точности средства измерения, определяемая пределами допустимых основных и дополнительных погрешностей, а также другими факторами, влияющими на нее».

Сам по себе класс не является постоянной величиной измерения, потому что само измерение зачастую зависит от множества переменных: места измерения, температуры, влажности и других факторов, класс позволяет определить лишь только в каком диапазоне относительных погрешностей работает данный прибор.

Чтобы заранее оценить погрешность, которую измерит устройство, также могут использоваться нормативные справочные значения.

Относительная погрешность — это отношение абсолютной погрешности к модулю действительного приближенного показателя полученного значения, измеряется в %.

Абсолютная погрешность рассчитывается следующим образом:

∆=±a или ∆=(a+bx)

x – число делений, нормирующее значение величины

a, b – положительные числа, не зависящие от х

Абсолютная и приведенная погрешность рассчитывается по следующим формулам, см. таблицу ниже

Какие классы точности бывают, как обозначаются

Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.

Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

• 0,1, 0,2 – считается самым высоким классом
• 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
• 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков

Каким ГОСТом регламентируется точность приборов?

ГОСТ 8.401-80 «Классы точности средств измерений» общие требования. Нормативным документом устанавливаются общие положения классификации точностей измерительных приборов.

Как определить класс точности электроизмерительного прибора, формулы расчета

Чтобы определить класс точности, необходимо взглянуть на его корпус или инструкцию пользователя, в ней вы можете увидеть цифру, обведенную в круг, например, ① это означает, что ваш прибор измеряет величину с относительной погрешностью ±1%.

Но что делать если известна относительная погрешность и необходимо рассчитать класс точности, например, амперметра, вольтметра и т.д. Рассмотрим на примере амперметра: известна ∆x=базовая (абсолютная) погрешность 0,025 (см. в инструкции), количество делений х=12

Находим относительную погрешность:

Y= 100×0,025/12=0,208 или 2,08%

(вывод: класс точности – 2,5).

Следует отметить, что погрешность неравномерна на всем диапазоне шкалы, измеряя малую величину вы можете получить наибольшую неточность и с увеличением искомой величины она уменьшается, для примера рассмотрим следующий вариант:

Вольтметр с классом p=±2, верхний предел показаний прибора Xn=80В, число делений x=12

Предел абсолютной допустимой погрешности:

Относительная погрешность одного деления:

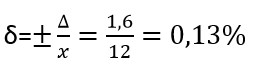
Если вам необходимо выполнить более подробный расчет, смотрите ГОСТ 8.401-80 п.3.2.6.

Поверка приборов, для чего она нужна

Все измерительные приборы измеряют с некой погрешностью, класс точности говорит лишь о том, в каком диапазоне она находится. Бывают случаи, когда диапазон погрешности незаметно увеличивается, и мы начинаем замечать, что измеритель «по-простому» начинает врать. В таких случаях помогает поверка.

Это процесс измерения эталонной величины в идеальных условиях прибором, обычно проводится метрологической службой или в метрологическом отделе предприятия производителя.

Существует первичная и периодическая, первичную проверку проводят после выпуска изделия и выдают сертификат, периодическую проводят не реже чем раз в год, для ответственных приборов чаще.

Поэтому если вы сомневаетесь в правильности работы устройства, вам следует провести его поверку в ближайшей метрологической службе, потому что измеритель может врать как в меньшую, так и в большую сторону.

Как легко проверить потребление электроэнергии в квартире, можете узнать в нашей статье.

Видео на тему относительная погрешность прибора

Заключение

Класс точности является важным показателем для каждого прибора, при выборе всегда обращайте внимание на него. Если вам нужен, например, электрический счетчик, важно чтобы он измерял потребление энергии с максимальной точностью, благодаря этому за весь период эксплуатации, вы сможете сэкономить приличную сумму средств.

Но, а если вам необходимо просто периодически проверять напряжение в розетке, для этого не стоит переплачивать за дорогостоящую покупку.

Источник

Методы повышения точности измерений

Анализ причин появления погрешностей измерений, выбор способов их обнаружения и уменьшения являются основными этапами процесса измерений. Погрешности измерений, принято делить на систематические и случайные. В процессе измерений систематические и случайные погрешности проявляются совместно и образуют нестационарный случайный процесс. Деление погрешностей на систематические и случайные является удобным приемом для их анализа и разработки методов уменьшения их влияния на результат измерения.

Рассмотрим способы обнаружения и исключения систематических погрешностей, поскольку они зависят от выбора метода измерений и его осуществелния.

По характеру изменения систематические погрешности делятся:

• постоянные – погрешности, связанные с неточной градуировкой шкалы прибора, отклонением размера меры от номинального значения, неточным выбором моделей объектов.
• переменные
  – периодические – погрешность изменяющаяся по периодическому закону, например погрешность отсчета при определении времени по башенным часам, если смотреть на стрелку снизу, температурная погрешность от изменения температуры в течение суток и т.п.
  – прогрессирующие – погрешности монотонно изменяющиеся (увеличивающиеся или уменьшающиеся) в общем случае по сложному, обычно неизвестному закону. Прогрессирующие погрешности во многих случаях обусловлены старением элементов средств измерений и могут быть скорректированы при его периодической поверке.

По причине возникновения погрешности измерений разделяются на три основные группы:

• методические – погрешности обусловленные неадекватностью принимаемых моделей реальным объектам, несовершенством методов измерений, упрощением зависимостей, положенных в основу измерений, неопределенностью объекта измерения;
• инструментальные – погрешности обусловленные прежде всего особенностями используемых в средствах измерений принципов и методов измерений, а также схемным, конструктивным и технологическим несовершенством средств измерений.
• взаимодейтствия – обусловлены взаимным влиянием средства измерений, объекта исследования и экспериментатора. Погрешности из-за взаимного влияния средства и объекта измерений обычно принято относить к методическим погрешностям, а погрешности, связанные с действиями экспериментатора, называются личными погрешностями. Однако такая классификация недостаточно полно отражает суть рассматриваемых погрешностей.

Выявление и устранение причин возникновения погрешностей – наиболее распространенный способ уменьшения всех видов систематических погрешностей. Примерами такого способа являются: термостатирование отдельных узлов или прибора в целом, а также проведение измерений в термостатированных помещениях для исключения температурной погрешности, применение экранов, фильтров и специальных цепей (например, эквипотенциальных цепей) для устранения погрешностей из-за влияния электромагнитных полей, наводок и токов утечек, применение стабилизированных источников питания.

Для уменьшения прогрессирующей погрешности из-за старения элементов средств измерений, параметры таких элементов стабилизируют путем искусственного и естественного старения. Кроме этого систематические погрешности можно уменьшить рациональным расположением средств измерений по отношению друг к другу, к источнику влияющих воздействий и к объекту исследования. Например магнитоэлектрические приборы должны быть удалены друг от друга, оси катушек индуктивности, должны быть расположены под углом 90°, выводы термопары должны располагаться по изотермическим линиям объекта.

Многие систематические погрешности, являющиеся не изменяющимися во времени функциями влияющих величин или обусловленные стабильными физическими эффектами, могут быть теоретически рассчитаны и устранены введением поправок или использованием специальных корректирующих цепей.

Другим радикальным способом устранения систематических погрешностей является поверки средств измерений в рабочих условиях с целью определения поправок к результатам измерения. Это дает возможность учесть все систематические погрешности без выяснения причин их возникновения. Степень коррекции систематических погрешностей в этом случае, естественно, зависит от метрологических характеристик используемых эталонных приборов и случайных погрешностей поверяемых приборов.

Фактически поверка средств измерений перед их использованием и введение поправок адекватна применению средств измерений более высоких классов точности при условии, что случайные погрешности средств измерений малы по сравнению с систематическими, а сами систематические погрешности медленно изменяются во времени.

Метод инвертирования широко используется для устранения ряда постоянных и медленно изменяющихся систематических погрешностей. Этот метод и ряд его разновидностей (метод исключения погрешности по знаку, коммутационного инвертирования, структурной модуляции, двукратных измерений, инвертирования функции преобразования и др.) основаны на выделении алгебраической суммы чесного числа сигналов измерительной информации, которые вследствие инвертирования отличаются направлением информативного сигнала, опорного сигнала или знаком погрешности.

Метод модуляции – метод близкий к методу инвертирования, в котором производится периодическое инвертирование входного сигнала и подавление помехи, имеющей однонаправленное действие.

Метод исключения погрешности по знаку — вариант метода инвертирования, который часто применяется для исключения известных по природе погрешностей, источники которых имеют направленное действие, например погрешностей из-за влияния постоянных магнитных полей, ТЭДС и др.

Метод замещения (метод разновременного сравнения) является наиболее универсальным методом, который дает возможность устранить большинство систематических погрешностей. Измерения осуществляются в два приема. Сначала по отсчетному устройству прибора делают отсчет измеряемой величины, затем, сохраняя все условия эксперимента неизменными, вместо измеряемой величины на вход прибора подают известную величину, значение которой с помощью регулируемой меры (калибратором) устанавливают таким образом, чтобы показание прибора было таким же, как при включении измеряемой величины.

Метод равномерного компарирования является разновидностью метода замещения, он используется при измерениях таких величин, которые нельзя с высокой точностью воспроизводить с помощью регулируемых мер или других технических средств. Обычно это величины, изменяющиеся с высокой частотой или по сложному закону. В качестве известных регулируемых величин при этом используются величины такого же рода, как измеряемые, но отличаютщиеся от них спектральным составом (обычно постоянные во времени и в пространстве) и создающие такой же, как и измеряемая величина, сигнал на выходе компарирующего преобразователя.

Метод эталонных сигналов заключается в том, что на вход средств измерений периодически вместо измеряемой величины подаются эталонные сигналы такого же рода, что и измеряемая величина. Разность между реальной градуировочной характеристикой используется для коррекции чувствительности или для автоматического введения поправки в результат измерения. При этом, как и при методе замещения, устраняются все систематические погрешности, но только в тех точках диапазона измерений, которые соответствуют эталонным сигналам. Метод широко используется в современных точных цифровых приборах и в информационно-измерительных системах. Примером использования этого метода является периодическая подстройка рабочего тока в компенсаторах и цифровых вольтметрах постоянного тока при помощи нормального элемента.

Тестовый метод – при использовании данного метода значение измеряемой величины определяется по результатам нескольких наблюдений, при которых в одном случае входным сигналом средства измерений является сама измеряемая величина Х, а в других – так называемые тесты, являющиеся функциями измеряемой величины.

Метод вспомагательных измерений используется для исключения погрешностей из-за влияющих величин и неинформативных параметров входного сигнала. Для реальзации этого метода одновременно с измеряемой величиной Х с помощью вспомогательных измерительных устройств производится измерение каждой из влияющих величин и вычисление с помощью вычислительного устройства, а также формул и алгоритмов поправок к результатам измерения.

Метод симметричных наблюдений заключается в проведении многократных наблюдений через равные промежутки времени и усреднении результатов наблюдений, симметрично расположенных относительно среднего наблюдения. Обычно этот метод применяется для исключения прогрессирующих погрешностей, изменяющихся по линейному закону. Так, при измерении сопротивления резистора путем сравнения напряжения на измеряемом и эталонном резисторах, включенных последовательно и питаемых от общего аккумулятора, может возникнуть погрешность вследствие разряда источника питания.
Для исключения этой погрешности проводят три измерения падения напряжения:

• на эталонном резисторе U01 = I·R0;
• через равные промежутки времени на измеряемом резисторе UX = (I — ΔI1)·RX;
• снова на эталонном резисторе U02 = (I — ΔI2)·R0.
• Если ток изменяется во времени по линейному закону, то ΔI2 = 2ΔI1; I — ΔI1 = (U01 + U02) / (2R0) и RX = R0·2·UX / (U01 + U02).

Метод симметричных наблюдений можно также использовать для устранения других видов погрешностей, например систематических погрешностей из-за влияющих величин, изменяющихся по периодическому закону. В этом случае симметричные наблюдения проводят через половину периода, когда погрешность имеет разные знаки, но одинаковые значения. Таким образом, например, можно исключить погрешность из-за наличия четных гармоник при измерении амплитудного значения напряжения при искаженной форме кривой.

Источник